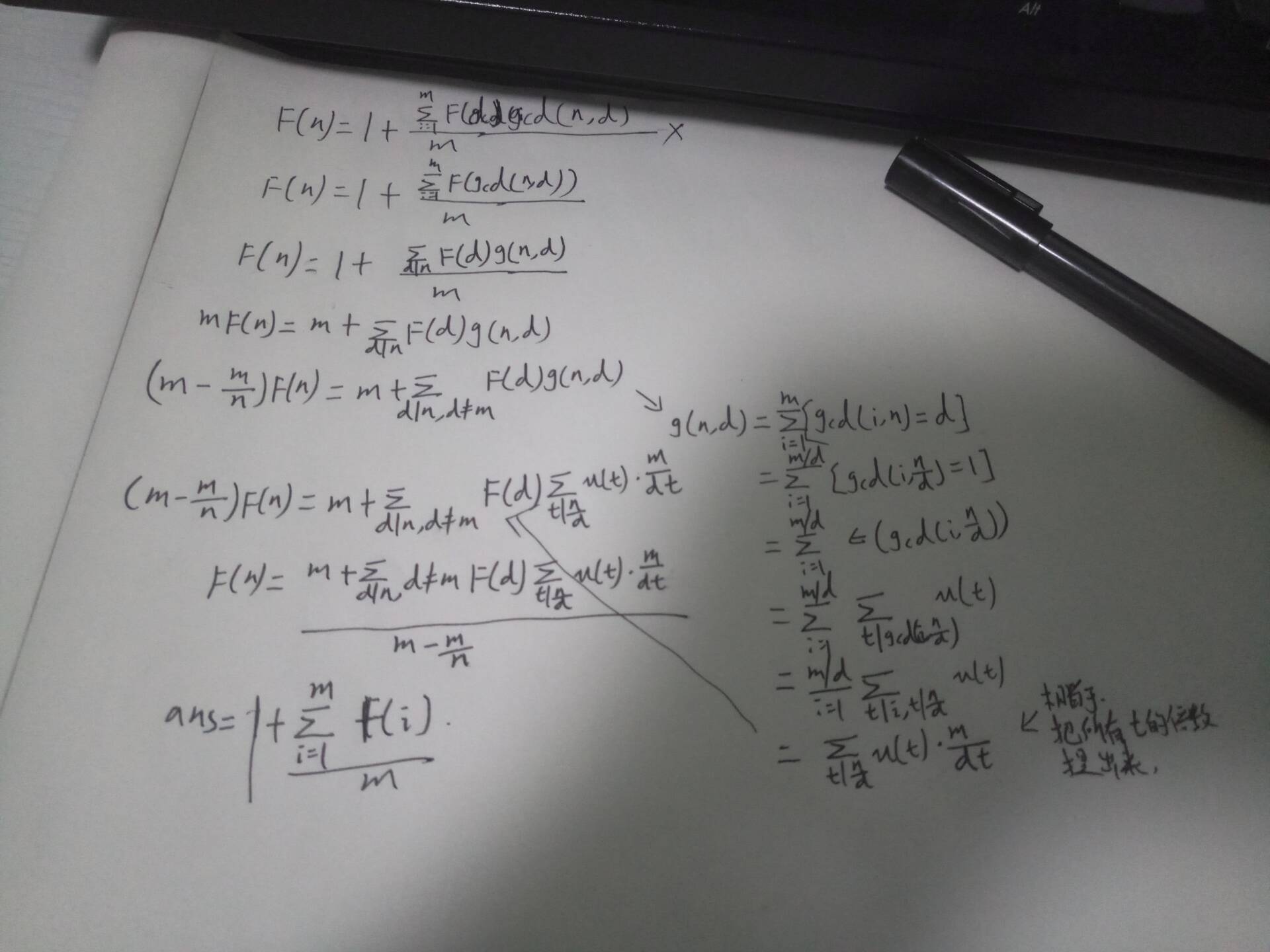A.HDU2222 Keywords Search
模板题。给出N个单词,后给你一个长串,问长串中有几个单词。
1 |
|
B.HDU2896 病毒侵袭
和A题一样的模板题,不过要求我们计算长串中出现了那些字符串,在ac自动机的end数组改成是哪一个字符串的编号然后在查询的时候用used数组记录一下既可。
注意是字符串不仅仅包括字母所以数组开开到128
1 |
|
C.HDU3065 病毒侵袭持续中
这题和B题一样的题意只不过题面很坑
1 |
|
D.ZOJ3430 Detect the Virus
题意
给你N个病毒(大小不超过64bytes子串)然后给你M个长串(大小不超过2048byte)问你长串没处理中有几个没处理的子串;
这里的子串和长串都是经过题目要求处理后的串
处理要求是原本的串的每个字符都是二进制长度为八位,然后合并在一起六位二进制组成一个新的字符,如果末尾缺了两位就添加一个’=’字符
例如:假设ab的八位二进制为10101000 01100101
现在合并成101010 000110 0101
变成(F,P,E)
因为后面的0101缺少了两位所以补一个’=’所以最终字符串为FPE=;
解法
这题的难点在于把字符串根据题目要求模拟成变化前的样子,然后就是AC自动机板子题;
我们可以把开始的字符串去掉’=’然后把字符串的每个字符变成数字(这样好变成二进制的数字处理)然后把
1.第一个数字取后面六位,第二个数字取前面两位;</br >
2.第二个数字取后面四位,第三个数字取前面四位;</br >
3.第三个数字取后面两位,第四个数字取前面六位;</br >
这样就四个数字一组组成三个八位的数字;
1 |
|
E.POJ2778 DNA Sequence
题意
给你N个病毒,问你有长度为L的DNA中有多少种是没有病毒的
思路
所有病毒串构造一个AC自动机,这个AC自动机可以看作一张有向图,图上的每个顶点就是Trie树上的结点,每个结点都可以看作是某个病毒串的前缀,Trie树的根则是空字符串。
而从根出发,在AC自动机上跑,经过k次转移到达某个结点,这个结点所代表的病毒串前缀可以看作长度为k的字符串的后缀,如果接下去跑往ATCG四个方向转移,就能到达新的结点,转移到新的长k+1字符串的后缀。
这样带着一个后缀状态的转移就能绕开病毒串,所以病毒串末尾的结点要标记,后缀存在病毒串的结点也要标记(这个在计算结点fail的时候就能处理),转移时就不能转移到被标记的结点。
接下来,题目的数据范围是10个长度10的病毒串,所以Trie树中最多101左右个结点,那么AC自动机整个转移就可以构建一张101*101的邻接矩阵,矩阵i行j列的权值是结点i转移到结点j的方案数。
而进行k次转移,从结点i转移到结点j的方案数是这个矩阵的k次幂,这个结论离散数学的图论有..
所以,长度n的字符串的方案数,就是转移n次根结点能到所有结点的方案和就是答案。就是计算矩阵的n次幂,统计根所在行的数字和,n的达到20亿用矩阵快速幂即可。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151对于agc、c而言,如果我zou过 a-g-c-d 这个路径。
root
/ \
a c
/
g
/
c
/
d
由上面这个图可知 左边的d 和 右边的c都是危险节点。 但漏掉了左边上的c
所以如果fail指针指向那个节点是危险节点的话,那么当前节点也是危险节点
using namespace std;
typedef long long ll;
const ll mod=100000;
const int maxn=10*10+5;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
struct Matrix{
unsigned long long mat[maxn][maxn];
int n;
Matrix(){}
Matrix(int _n){
n=_n;
for(int i=0;i<n;i++)for(int j=0;j<n;j++)mat[i][j]=0;
}
Matrix operator *(const Matrix &b)const{
Matrix ret=Matrix(n);
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
for(int k=0;k<n;k++){
ret.mat[i][j]+=(mat[i][k]*b.mat[k][j])%mod;
ret.mat[i][j]%=mod;
}
}
}
return ret;
}
unsigned long long pow_m(unsigned long long a,int n){
unsigned long long ret=1,tmp=a;
while(n){
if(n&1)ret*=tmp;
tmp*=tmp;
n>>=1;
}return ret;
}
Matrix pow_M(Matrix a,ll n){
Matrix ret=Matrix(a.n);
for(int i=0;i<a.n;i++)ret.mat[i][i]=1;
Matrix tmp=a;
while(n){
if(n&1)ret=ret*tmp;
tmp=tmp*tmp;
n>>=1;
}
return ret;
}
};
struct Trie{
int next[maxn][4],fail[maxn],id['Z'+1];
bool end[maxn];
int root,L;
int newnode(){
for(int i=0;i<4;++i)next[L][i]=-1;
end[L++]=false;
return L-1;
}
void init(){
L=0;
id['A']=0;id['T']=1;id['C']=2;id['G']=3;
root=newnode();
}
void insert(char buf[]){
int len=strlen(buf);
int now=root;
for(int i=0;i<len;i++){
if(next[now][id[buf[i]]]==-1)next[now][id[buf[i]]]=newnode();
now=next[now][id[buf[i]]];
}
end[now]=true;
}
void build(){
queue<int>Q;
fail[root]=root;
for(int i=0;i<4;i++)
if(next[root][i]==-1)next[root][i]=root;
else{
fail[next[root][i]]=root;
Q.push(next[root][i]);
}
while(!Q.empty()){
int now=Q.front();
Q.pop();
if(end[fail[now]])end[now]=true;
for(int i=0;i<4;i++)
if(next[now][i]==-1)
next[now][i]=next[fail[now]][i];
else{
fail[next[now][i]]=next[fail[now]][i];
Q.push(next[now][i]);
}
}
}
Matrix getMatrix(){
Matrix ret=Matrix(L);
for(int i=0;i<L;i++){
for(int j=0;j<4;j++){
if(end[next[i][j]]==false&&end[i]==false)
ret.mat[i][next[i][j]]++;
}
}
return ret;
}
};
Trie ac;
char buf[15];
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
int n;
ll L;
cin>>n>>L;
ac.init();
for(int i=0;i<n;i++){
cin>>buf;
ac.insert(buf);
}
ac.build();
Matrix mat=ac.getMatrix();
mat=mat.pow_M(mat,L);
ll ans=0;
for(int i=0;i<mat.n;i++){
ans=(ans+mat.mat[0][i])%mod;
}
cout<<ans<<endl;
return 0;
}
F.HDU2243 考研路茫茫――单词情结
题意
跟上题一样,不过这题是让你求包括的个数,而且不仅仅是长度为L而且长度小于L的也要包括进去;可以通过上题很快求出不包括的,然后求和,在求出全部的26^1+…26^L的个数减去不包括的就是答案;
思路
通过矩阵求出全部长度的可能和AC自动机求出来的矩阵的和,然后相减1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const ll mod=2147483648LL;
const ll maxn=5*6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
struct Matrix{
unsigned long long mat[maxn][maxn];
int n;
Matrix(){}
Matrix(int _n){
n=_n;
for(int i=0;i<n;i++)for(int j=0;j<n;j++)mat[i][j]=0;
}
Matrix operator *(const Matrix &b)const{
Matrix ret=Matrix(n);
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
for(int k=0;k<n;k++){
ret.mat[i][j]+=(mat[i][k]*b.mat[k][j]);
}
}
}
return ret;
}
unsigned long long pow_m(unsigned long long a,int n){
unsigned long long ret=1,tmp=a;
while(n){
if(n&1)ret*=tmp;
tmp*=tmp;
n>>=1;
}return ret;
}
Matrix pow_M(Matrix a,ll n){
Matrix ret=Matrix(a.n);
for(int i=0;i<a.n;i++)ret.mat[i][i]=1;
Matrix tmp=a;
while(n){
if(n&1)ret=ret*tmp;
tmp=tmp*tmp;
n>>=1;
}
return ret;
}
};
struct Trie{
int next[maxn][26],fail[maxn];
bool end[maxn];
int root,L;
int newnode(){
for(int i=0;i<26;++i)next[L][i]=-1;
end[L++]=false;
return L-1;
}
void init(){
L=0;
root=newnode();
}
void insert(char buf[]){
int len=strlen(buf);
int now=root;
for(int i=0;i<len;i++){
if(next[now][buf[i]-'a']==-1)next[now][buf[i]-'a']=newnode();
now=next[now][buf[i]-'a'];
}
end[now]=true;
}
void build(){
queue<int>Q;
fail[root]=root;
for(int i=0;i<26;i++)
if(next[root][i]==-1)next[root][i]=root;
else{
fail[next[root][i]]=root;
Q.push(next[root][i]);
}
while(!Q.empty()){
int now=Q.front();
Q.pop();
if(end[fail[now]])end[now]=true;
for(int i=0;i<26;i++)
if(next[now][i]==-1)
next[now][i]=next[fail[now]][i];
else{
fail[next[now][i]]=next[fail[now]][i];
Q.push(next[now][i]);
}
}
}
Matrix getMatrix(){
Matrix ret=Matrix(L+1);
for(int i=0;i<L;i++){
for(int j=0;j<26;j++){
if(end[next[i][j]]==false)
ret.mat[i][next[i][j]]++;
}
}
for(int i=0;i<L+1;i++)ret.mat[i][L]=1;
return ret;
}
};
Trie ac;
char buf[15];
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
int n;
ll L;
while(cin>>n>>L){
ac.init();
for(int i=0;i<n;i++){
cin>>buf;
ac.insert(buf);
}
ac.build();
Matrix mat=ac.getMatrix();
mat=mat.pow_M(mat,L);
ull res=0;
for(int i=0;i<mat.n;i++)res+=mat.mat[0][i];
res--;
ull ans=0;
Matrix all=Matrix(2);all.mat[0][0]=26;all.mat[0][1]=all.mat[1][1]=1;
/*
26 1 × Sn -> Sn+1
0 1 × 26 -> 26
*/
all=all.pow_M(all,L);
ans=all.mat[0][1]*26;
cout<<ans-res<<endl;
}
return 0;
}
G.POJ - 1625 Censored!
题意
n,m,p;n代表总共有n个字母,m代表字符串的长度为m,p代表病毒字符串的个数;题目让你求的是不包含病毒的字符串长度为m的个数为多少。
题解
较麻烦的题,但是不要被代码长度吓到了
先讲一讲思路,给出了可用字母和不可用单词,
那么首先想到将不可用单词建立AC自动机。
那么什么情况下会用到禁止使用的单词呢?
我们将Trie树中间被标记的点叫做危险结点。
在AC自动机中不断遍历,如果遇到危险结点,就是不合法的
考虑如何遍历,这里需要用到AC自动机建立失败指针的一个技巧:
若当前结点无儿子结点,把失败指针处的儿子拿过来。
如果当前结点有儿子结点,把失败指针处的危险标记拿过来,详细见代码。
这样就方便了后面找后继结点。
不过没有取模操作,需要大数。
大数不可以矩阵快速幂吗?内存不够……
使用dp递推,递推公式也比较简单。
1 |
|
H.HDU - 2825 Wireless Password
题意
给你一堆(不超过10个)长度不超过10的单词,然后问你长度为N句子并且包含K个不同单词的个数有多少个;
题解
先利用ac自动机求出各种状态,(总共不超过1010)个,然后dp枚举长度,状态,和已有个数,*已有个数可以用状态压缩O(1)求出来
1 |
|
I.HDU - 2296 Ring
题意
1 | 给定m个不同的单词,单词由小写字母组成,每个单词都有自身的价值。现在你要设计一个字符串,字符串的长度不能超过n。如果字符串里面包含了某个单词,就可以获得相应的价值,价值可以重复计算。单词可以相互重叠。 |
题解
模板AC自动机,不过加了个字符串储存 不过不知道这是不是就是传说中的trie图
1 |
|
J.HDU - 2457 DNA repair
题意
给你N个病毒串,然后给你一个长度为N的基因串,让你替换成没有病毒的基因串,求最小的替换次数(每次只能替换一个字符)
题解
DP I ,J I: 当前串的长度,J,结尾的位置
直接DP扫过去,用AC自动机构造出病毒的节点,然后开始构造,如果新的点和原来的串相同就
否则
1 |
|
K.ZOJ - 3228 Searching the String
题意
先给你一个字符串,然后给你若干个子串,0代表能够重叠,1代表不能重叠,求出如今母串的次数。
题解
多一个推断的是假设这个子串与上次出现的次数大于子串长度的话。就代表这次不是重叠的了
1 |
|
L.HDU - 3341 Lost’s revenge
题意
给出N个模式串(len<=10)和一个目标长串(len<=40)求将目标串重新排列后所能包含的模式串个数
题解
首先重排列,所以目标串中的ACGT个数不能变化
刚开始想开个五维数组来存取状态,但是空间会爆炸;
所以搜了一下发现可以用模拟进制来把 ACGT的个数用一个数字表达
1 |
|
M.HDU - 3247 Resource Archiver
题意
给定n个文本串,m个病毒串,文本串重叠部分可以合并,但合并后不能含有病毒串,问所有文本串合并后最短多长。
思路
把病毒和文本出串塞入AC自动机中,然后把每个文本串的结点 和另一个文本串的结点的最短路求出来,在用状态DP求出每个点到另一个点之间的距离
1 |
|
N.ZOJ - 3494 BCD Code
题意
跟数位DP的一题重复了 这里再做一次
1 |
|
O.HDU - 4758 Walk Through Squares
题意
给你一个n*m的网格,现在你要从(1,1)走到(n,m),每次只能向右走或者向下走,走完后会形成一个包含R,D的序列,这个序列必须要包含题目给出的两个字符串,问有多少种方案。
题解
由于要从(1,1)走到(n,m),所以这个形成的字符串包含R和D的数量是一定的。
现在考虑dp i j k sta,表示包含两种串的组合状态,走了i个D,走了j个R,走到了k这个AC自动机的节点的方案数,串1和串2的状态sta 然后dp一下就行了。复杂度为O(3×n×m×len(s1)×len(s2))
按理说应该是N个D M个R 可是这样我就错了,换一下才AC。。。
1 |
|
P.HDU - 4511 小明系列故事――女友的考验
题意中文题
题解
设dp i j 表示到第i个点,自动机状态到j的最小步数,注意的是因为我们是根据不合法的路径构造自动机的,所以我们是不能走到某一条路径的末尾的,根据这点来记录我们的终止条件
1 |
|
Q.附加题1 牛客网暑期ACM多校训练营(第九场)- Typing practice
题意
有n(n<=4)个长度为len的字符串,以及一个长度为len2的操作串。每一次你将选取操作串中长度为i(0<=i<=len2)的前缀,问你最少在这个前缀后加多少个字符,使得新字符串的后缀中能够至少出现这n个字符串中的一个。
题解
因为题目中设计多个串的匹配一个长串的问题,我们可以考虑使用AC自动机进行处理。
再考虑题目中要求我们求出匹配串的后缀凑出模式串的最小长度,因此,我们可以将这样的一个问题转化成:在一个Trie图中,处于第i个结点的字符到达任意一个模式串终点j的最短路。
因此,我们只需要利用AC自动机,将利用失配指针的性质,先将整张Trie图建立出来,并将每一个结点到达任意终点的最短路用bfs求出即可。
1 |
|