洛谷试炼场 4-23 莫比乌斯反演

Diposting di 2019-04-24 | Edited on 2019-02-13

P2257 YY的GCD

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e7+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
bool vis[maxn];
ll sum[maxn];
int prim[maxn];
int mu[maxn],g[maxn];
int cnt;
void get_mu(int n){
    mu[1]=1;
    for(int i=2;i<=n;i++)
    {
        if(!vis[i]){mu[i]=-1;prim[++cnt]=i;}
        for(int j=1;j<=cnt&&prim[j]*i<=n;j++)
        {
            vis[i*prim[j]]=1;
            if(i%prim[j]==0)break;
            else mu[prim[j]*i]=-mu[i];
        }
    }
    for(int j=1;j<=cnt;j++)
        for(int i=1;i*prim[j]<=n;i++)g[i*prim[j]]+=mu[i];
    for(int i=1;i<=n;i++)sum[i]=sum[i-1]+g[i];
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    get_mu(10000000);
    int t;
    cin>>t;
    while(t--){
        int n,m;
        cin>>n>>m;
        if(n>m)swap(n,m);
        ll ans=0;
        for(int l=1,r;l<=n;l=r+1){
            r=min(n/(n/l),m/(m/l));
            ans+=1LL*(n/l)*(m/l)*(sum[r]-sum[l-1]);
        }
        cout<<ans<<endl;
    }
    return 0;
}

[POI2007]ZAP-Queries

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e5+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
bool vis[maxn];
ll sum[maxn];
int prim[maxn];
int mu[maxn],g[maxn];
int cnt;
void get_mu(int n){
    mu[1]=1;
    for(int i=2;i<=n;i++)
    {
        if(!vis[i]){mu[i]=-1;prim[++cnt]=i;}
        for(int j=1;j<=cnt&&prim[j]*i<=n;j++)
        {
            vis[i*prim[j]]=1;
            if(i%prim[j]==0)break;
            else mu[prim[j]*i]=-mu[i];
        }
    }
    for(int i=1;i<=n;i++)sum[i]=sum[i-1]+mu[i];
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    get_mu(50000);
    int t;
    cin>>t;
    while(t--){
        int a,b,d;
        cin>>a>>b>>d;
        int mx=min(a/d,b/d);
        ll ans=0;
        for(int l=1,r;l<=mx;l=r+1){
            r=min((a/d)/((a/d)/l),(b/d)/((b/d)/l));
            ans+=(ll)((a/d)/l)*((b/d)/l)*(sum[r]-sum[l-1]);
        }
        cout<<ans<<endl;
    }
    return 0;
}

P3327 [SDOI2015]约数个数和

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e5+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
bool vis[maxn];
ll sum[maxn];
int prim[maxn];
int mu[maxn];
ll g[maxn];
int cnt;
void get_mu(int n){
    mu[1]=1;
    for(int i=2;i<=n;i++)
    {
        if(!vis[i]){mu[i]=-1;prim[++cnt]=i;}
        for(int j=1;j<=cnt&&prim[j]*i<=n;j++)
        {
            vis[i*prim[j]]=1;
            if(i%prim[j]==0)break;
            else mu[prim[j]*i]=-mu[i];
        }
    }
    for(int i=1;i<=n;i++)sum[i]=sum[i-1]+mu[i];
    for(int i=1;i<=n;i++){
        ll ans=0;
        for(int l=1,r;l<=i;l=r+1){
            r=(i/(i/l));
            ans+=1LL*(r-l+1)*1LL*(i/l);
        }
        g[i]=ans;
    }
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    get_mu(50000);
    int t;
    cin>>t;
    while(t--){
        int n,m;
        cin>>n>>m;
        int mx=min(n,m);
        ll ans=0;
        for(int l=1,r;l<=mx;l=r+1){
            r=min(n/(n/l),m/(m/l));
            ans+=(1LL*g[n/l]*1LL*g[m/l])*1LL*(sum[r]-sum[l-1]);
        }
        cout<<ans<<endl;
    }
    return 0;
}

P2522 [HAOI2011]Problem b

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e5+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
bool vis[maxn];
ll sum[maxn];
int prim[maxn];
int mu[maxn];
ll g[maxn];
int cnt;
int k;
void get_mu(int n){
    mu[1]=1;
    for(int i=2;i<=n;i++)
    {
        if(!vis[i]){mu[i]=-1;prim[++cnt]=i;}
        for(int j=1;j<=cnt&&prim[j]*i<=n;j++)
        {
            vis[i*prim[j]]=1;
            if(i%prim[j]==0)break;
            else mu[prim[j]*i]=-mu[i];
        }
    }
    for(int i=1;i<=n;i++)sum[i]=sum[i-1]+mu[i];
}
ll get(int a,int b){
    int mx=min(a,b);
    ll ans=0;
    for(int l=1,r;l<=mx;l=r+1){
        r=min(a/(a/l),b/(b/l));
        ans+=(1ll*a/(1ll*l*k))*(1ll*b/(1ll*l*k))*(sum[r]-sum[l-1]);
    }
    return ans;
}
// 适用于正负整数
template <class T>
inline bool read(T &ret)
{
    char c;
    int sgn;
    if (c = getchar(), c == EOF) return 0; //EOF
    while (c != '-' && (c < '0' || c > '9')) c = getchar();
    sgn = (c == '-') ? -1 : 1;
    ret = (c == '-') ? 0 : (c - '0');
    while (c = getchar(), c >= '0' && c <= '9') ret = ret * 10 + (c - '0');
    ret *= sgn;
    return 1;
}
inline void out(ll x)
{
    if (x > 9) out(x / 10);
    putchar(x % 10 + '0');
}
int main()
{
   /* std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);*/
    get_mu(50000);
    int t;
    //cin>>t;
    read(t);
    while(t--){
        int a,b,c,d;
       // cin>>a>>b>>c>>d>>k;
       read(a);read(b);read(c);read(d);read(k);
        out(get(b,d)-get(b,c-1)-get(a-1,d)+get(a-1,c-1));
        puts("");
    }
    return 0;
}

洛谷试炼场 4-17 树链剖分

Diposting di 2019-04-24 | Edited on 2019-02-09

[ZJOI2008]树的统计（入门题,链最大值,链和）

思路

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int n,q,a[maxn];
vector<int>G[maxn];
int size[maxn],son[maxn],fa[maxn],dep[maxn],top[maxn];
int id[maxn],pre[maxn],cnt=0;
void dfs1(int u,int f,int deep){
    size[u]=1;
    fa[u]=f;son[u]=0;dep[u]=deep;
    for(int i=0;i<G[u].size();i++){
        int v=G[u][i];
        if(v==f)continue;
        dfs1(v,u,deep+1);
        size[u]+=size[v];
        if(size[v]>size[son[u]])son[u]=v;
    }
}
void dfs2(int u,int root){
    id[u]=++cnt;top[u]=root;pre[cnt]=u;
    if(son[u])dfs2(son[u],root);
    for(int i=0;i<G[u].size();i++){
        int v=G[u][i];
        if(v==fa[u]||v==son[u])continue;
        dfs2(v,v);
    }
}
int sumv[maxn<<2],maxv[maxn<<2];
inline void pushup(int o){
    sumv[o]=sumv[o<<1]+sumv[o<<1|1];
    maxv[o]=max(maxv[o<<1],maxv[o<<1|1]);
}
void build(int o,int l,int r){
    int mid=(l+r)/2;
    if(l==r){
        sumv[o]=maxv[o]=a[pre[l]];return;
    }
    build(o<<1,l,mid);build(o<<1|1,mid+1,r);
    pushup(o);
}
void update(int o,int l,int r,int q,int v){
    int mid=(l+r)/2;
    if(l==r){
        sumv[o]=maxv[o]=v;return;
    }
    if(q<=mid)update(o<<1,l,mid,q,v);
    else update(o<<1|1,mid+1,r,q,v);
    pushup(o);
}
int querysum(int o,int l,int r,int ql,int qr){
    int mid=(l+r)/2,ans=0;
    if(ql<=l&&r<=qr)return sumv[o];
    if(ql<=mid)ans+=querysum(o<<1,l,mid,ql,qr);
    if(qr>mid)ans+=querysum(o<<1|1,mid+1,r,ql,qr);
    return ans;
}
int querymax(int o,int l,int r,int ql,int qr){
    int mid=(l+r)/2,ans=-inf;
    if(ql<=l&&r<=qr)return maxv[o];
    if(ql<=mid)ans=max(ans,querymax(o<<1,l,mid,ql,qr));
    if(qr>mid)ans=max(ans,querymax(o<<1|1,mid+1,r,ql,qr));
    return ans;
}
int qsum(int u,int v){
    int ans=0;
    while(top[u]!=top[v]){
        if(dep[top[u]]<dep[top[v]])swap(u,v);
        ans+=querysum(1,1,n,id[top[u]],id[u]);
        u=fa[top[u]];
    }
    if(dep[u]<dep[v])swap(u,v);
    ans+=querysum(1,1,n,id[v],id[u]);
    return ans;
}
int qmax(int u,int v){
    int ans=-inf;
    while(top[u]!=top[v]){
        if(dep[top[u]]<dep[top[v]])swap(u,v);
        ans=max(ans,querymax(1,1,n,id[top[u]],id[u]));
        u=fa[top[u]];
    }
    if(dep[u]<dep[v])swap(u,v);
    ans=max(ans,querymax(1,1,n,id[v],id[u]));
    return ans;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    cin>>n;
    for(int i=1;i<n;i++){
        int u,v;
        cin>>u>>v;G[u].push_back(v);G[v].push_back(u);
    }
    for(int i=1;i<=n;i++)cin>>a[i];
    fa[1]=1;dfs1(1,0,1);dfs2(1,1);build(1,1,n);
    int q;
    cin>>q;
    while(q--){
        int x,y;char s[100];
        cin>>s>>x>>y;
        if(s[1]=='H')update(1,1,n,id[x],y);
        else if(s[1]=='M')cout<<qmax(x,y)<<endl;
        else if(s[1]=='S')cout<<qsum(x,y)<<endl;
    }
    return 0;
}

P2486 [SDOI2011]染色 (区间操作很难未AC)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int n,q,col[maxn];
vector<int>G[maxn];
int size[maxn],son[maxn],fa[maxn],dep[maxn],top[maxn];
int id[maxn],pre[maxn],cnt=0;
void dfs1(int u,int f,int deep){
    size[u]=1;
    fa[u]=f;son[u]=0;dep[u]=deep;
    for(int i=0;i<G[u].size();i++){
        int v=G[u][i];
        if(v==f)continue;
        dfs1(v,u,deep+1);
        size[u]+=size[v];
        if(size[v]>size[son[u]])son[u]=v;
    }
}
void dfs2(int u,int root){
    id[u]=++cnt;top[u]=root;pre[cnt]=u;
    if(son[u])dfs2(son[u],root);
    for(int i=0;i<G[u].size();i++){
        int v=G[u][i];
        if(v==fa[u]||v==son[u])continue;
        dfs2(v,v);
    }
}
struct node{
    int l,r;
    int num,lazy,lc,rc;
}my[maxn<<2];
void push_up(int o){
    my[o].lc=my[o<<1].lc;my[o].rc=my[(o<<1)|1].rc;
    int ans=my[o<<1].num+my[(o<<1)|1].num;
    if(my[o<<1].rc==my[(o<<1)|1].lc)ans--;
    my[o].num=ans;
}
void push_down(int o){
    if(my[o].lazy){
        my[o<<1].lazy=my[(o<<1)|1].lazy=my[o].lazy;
        my[o<<1].num=my[(o<<1)|1].num=1;
        my[o<<1].lc=my[o<<1].rc=my[o].lc;
        my[(o<<1)|1].lc=my[(o<<1)|1].rc=my[o].lc;
        my[o<<1].lazy=0;
    }
}
void build(int o,int l,int r){
    int mid=(l+r)/2;
    my[o].l=l;my[o].r=r;my[o].num=0;my[o].lazy=0;
    if(l==r){
        my[o].num=1;
        my[o].lc=my[o].rc=col[pre[l]];
        return;
    }
    build(o<<1,l,mid);build((o<<1)|1,mid+1,r);
    push_up(o);
}
void update(int o,int l,int r,int x){
    if(my[o].l==l&&my[o].r==r){
        my[o].num=my[o].lazy=1;
        my[o].lc=my[o].rc=x;
        return;
    }
    push_down(o);
    int mid=(my[o].l+my[o].r)/2;
    if(r<=mid)update(o<<1,l,r,x);
    else if(l>mid)update((o<<1)|1,l,r,x);
    else{
        update(o<<1,l,mid,x);update((o<<1)|1,mid+1,r,x);
    }
    push_up(o);
}
void uptree(int u,int v,int c){
    while(top[u]!=top[v]){
        if(dep[top[u]]<dep[top[v]])swap(u,v);
        update(1,id[top[u]],id[u],c);
        u=fa[top[u]];
    }
    if(dep[u]<dep[v])swap(u,v);
    update(1,id[v],id[u],c);
}
int lc,rc;
int query(int o,int l,int r,int L,int R){
    if(my[o].l==L)lc=my[o].lc;
    if(my[o].r==R)rc=my[o].rc;
    if(my[o].l==l&&my[o].r==r)return my[o].num;
    push_down(o);
    int mid=(my[o].l+my[o].r)/2;
    if(r<=mid)return query(o<<1,l,r,L,R);
    else if(l>mid)return query((o<<1)|1,l,r,L,R);
    else{
        int ans=query(o<<1,l,mid,L,R);
        ans+=query((o<<1)|1,mid+1,r,L,R);
        if(my[o<<1].rc==my[(o<<1)|1].lc)ans--;
        return ans;
    }
    push_up(o);
}
int qutree(int u,int v){
    int ans1=-1,ans2=-1,ans=0;
    while(top[u]!=top[v]){
        if(dep[top[u]]<dep[top[v]])swap(u,v),swap(ans1,ans2);
        ans+=query(1,id[top[u]],id[u],id[top[u]],id[u]);
        if(rc==ans1)ans--;
        ans1=lc;u=fa[top[u]];
    }
    if(dep[u]<dep[v])swap(u,v),swap(ans1,ans2);
    ans+=query(1,id[v],id[u],id[v],id[u]);
    if(rc==ans1)ans--;
    if(lc==ans2)ans--;
    return ans;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>col[i];
    for(int i=1;i<n;i++){
        int u,v;cin>>u>>v;
        G[u].push_back(v);G[v].push_back(u);
    }
    dfs1(1,1,1);dfs2(1,1);build(1,1,n);
    while(m--){
        char s[150];
        cin>>s;
        int x,y;
        if(s[0]=='C'){
            int c;cin>>x>>y>>c;
            uptree(x,y,c);
        }
        else{
            cin>>x>>y;
            cout<<qutree(x,y)<<endl;
        }
    }
    return 0;
}

P2146 [NOI2015]软件包管理器

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int n,q,col[maxn];
vector<int>G[maxn];
int size[maxn],son[maxn],fa[maxn],dep[maxn],top[maxn];
int id[maxn],pre[maxn],cnt=0;
void dfs1(int u,int f,int deep){
    size[u]=1;
    fa[u]=f;son[u]=0;dep[u]=deep;
    for(int i=0;i<G[u].size();i++){
        int v=G[u][i];
        if(v==f)continue;
        dfs1(v,u,deep+1);
        size[u]+=size[v];
        if(size[v]>size[son[u]])son[u]=v;
    }
}
void dfs2(int u,int root){
    id[u]=++cnt;top[u]=root;pre[cnt]=u;
    if(son[u])dfs2(son[u],root);
    for(int i=0;i<G[u].size();i++){
        int v=G[u][i];
        if(v==fa[u]||v==son[u])continue;
        dfs2(v,v);
    }
}
int sum[maxn<<2],lazy[maxn<<2];
void push_up(int o){
    sum[o]=sum[o<<1]+sum[o<<1|1];
}
void push_down(int o,int l,int r){
    if(lazy[o]){
        int mid=(l+r)/2;
        if(lazy[o]==-1)sum[o<<1]=sum[o<<1|1]=0,lazy[o<<1]=lazy[o<<1|1]=-1;
        else sum[o<<1]=mid-l+1,sum[o<<1|1]=r-mid,lazy[o<<1]=lazy[o<<1|1]=1;
        lazy[o]=0;
    }
}
void uninstall(int o,int l,int r,int ql,int qr,int x){
    if(ql<=l&&r<=qr){
        if(!x)lazy[o]=-1,sum[o]=0;
        else lazy[o]=1,sum[o]=r-l+1;return;
    }
    int mid=(l+r)/2;push_down(o,l,r);
    if(mid>=ql)uninstall(o<<1,l,mid,ql,qr,x);
    if(mid<qr)uninstall(o<<1|1,mid+1,r,ql,qr,x);
    push_up(o);
}
void install(int v,int x,int y){
    while(top[x]!=top[y]){
        if(dep[top[x]]<dep[top[y]])swap(x,y);
        uninstall(1,1,n,id[top[x]],id[x],v);
        x=fa[top[x]];
    }
    if(dep[x]<dep[y])swap(x,y);
    uninstall(1,1,n,id[y],id[x],v);
}

int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    cin>>n;
    for(int i=2;i<=n;i++){
        int u;
        cin>>u;u++;
        G[i].push_back(u);
        G[u].push_back(i);
    }
    dfs1(1,1,1);
    dfs2(1,1);
    int m;cin>>m;
    char op[150];
    while(m--){
        int x;
        cin>>op>>x;x++;int p=sum[1];
        if(op[0]=='i'){
            install(1,x,1);
            cout<<abs(p-sum[1])<<endl;
        }
        else{
            uninstall(1,1,n,id[x],id[x]+size[x]-1,0);
            cout<<abs(p-sum[1])<<endl;
        }
    }
    return 0;
}
/*
7
0 0 0 1 1 5
5
install 5
install 6
uninstall 1
install 4
uninstall 0
*/

P3258 [JLOI2014]松鼠的新家 (区间加减)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=3e5+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
vector<int>G[maxn];
int id[maxn],dep[maxn],pre[maxn],fa[maxn],size[maxn],son[maxn],cnt,top[maxn];
void dfs1(int now,int f,int deep){
    fa[now]=f;size[now]=1;son[now]=0;dep[now]=deep;
    for(auto i:G[now]){
        if(i==f)continue;
        dfs1(i,now,deep+1);
        size[now]+=size[i];
        if(size[i]>size[son[now]])son[now]=i;
    }
}
void dfs2(int now,int root){
    id[now]=++cnt;pre[cnt]=now;top[now]=root;
    if(son[now])dfs2(son[now],root);
    for(auto i:G[now]){
        if(i==fa[now]||i==son[now])continue;
        dfs2(i,i);
    }
}
int sum[maxn<<2],lazy[maxn<<2];
void push_up(int o){
    sum[o]=sum[o<<1]+sum[o<<1|1];
}
void push_down(int o,int l,int r){
    if(lazy[o]){
        int mid=(l+r)/2;
        lazy[o<<1]+=lazy[o];
        lazy[o<<1|1]+=lazy[o];
        sum[o<<1]+=(mid-l+1)*lazy[o];
        sum[o<<1|1]+=(r-mid)*lazy[o];
        lazy[o]=0;
    }
}
void update(int o,int l,int r,int ql,int qr,int w){
    int mid=(l+r)/2;
    if(ql<=l&&r<=qr){
        lazy[o]+=w;
        sum[o]+=(r-l+1)*w;
        return;
    }
    push_down(o,l,r);
    if(ql<=mid)update(o<<1,l,mid,ql,qr,w);
    if(qr>mid)update(o<<1|1,mid+1,r,ql,qr,w);
    push_up(o);
}
void print(int o,int l,int r,int ql,int qr){
    cout<<"o=="<<o<<" l="<<l<<" r="<<r<<" ql="<<ql<<" qr="<<qr<<endl;
    cout<<"sum="<<sum[o]<<endl;
}
int query(int o,int l,int r,int ql,int qr){
    //print(o,l,r,ql,qr);
    if(l==r){
        return sum[o];
    }
    int mid=(l+r)/2;
    push_down(o,l,r);
    if(ql<=mid)return query(o<<1,l,mid,ql,qr);
    else return query(o<<1|1,mid+1,r,ql,qr);
}
void uptree(int u,int v,int w){
    while(top[u]!=top[v]){
        if(dep[top[u]]<dep[top[v]])swap(u,v);
        update(1,1,cnt,id[top[u]],id[u],w);
        u=fa[top[u]];
    }
    if(dep[u]<dep[v])swap(u,v);
    update(1,1,cnt,id[v],id[u],w);
}
int a[maxn];
// 适用于正负整数
template <class T>
inline bool read(T &ret)
{
    char c;
    int sgn;
    if (c = getchar(), c == EOF) return 0; //EOF
    while (c != '-' && (c < '0' || c > '9')) c = getchar();
    sgn = (c == '-') ? -1 : 1;
    ret = (c == '-') ? 0 : (c - '0');
    while (c = getchar(), c >= '0' && c <= '9') ret = ret * 10 + (c - '0');
    ret *= sgn;
    return 1;
}
inline void out(int x)
{
    if (x > 9) out(x / 10);
    putchar(x % 10 + '0');
}
int main()
{
   /* std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);*/
    int n;
    //cin>>n;
    read(n);
    for(int i=1;i<=n;i++)cin>>a[i];
    for(int i=1;i<n;i++){
        int u,v;
       // cin>>u>>v;
        read(u);read(v);
        G[u].push_back(v);
        G[v].push_back(u);
    }
    dfs1(1,1,1);dfs2(1,1);
    for(int i=1;i<n;i++){
        uptree(a[i],a[i+1],1);
        uptree(a[i+1],a[i+1],-1);
    }
    for(int i=1;i<=n;i++){
       // cout<<query(1,1,n,id[i],id[i])<<endl;
        out(query(1,1,n,id[i],id[i]));
        puts("");
    }
    return 0;
}

洛谷试炼场 4-17 主席树

Diposting di 2019-04-24 | Edited on 2019-02-10

P3834 【模板】可持久化线段树 1（主席树）

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int n,m,cnt,root[maxn],a[maxn],x,y,k;
struct node{int l,r,sum;}T[maxn*20];
vector<int>v;
int getid(int x){return lower_bound(v.begin(),v.end(),x)-v.begin()+1;}
void update(int l,int r,int &x,int y,int pos){
    T[++cnt]=T[y],T[cnt].sum++,x=cnt;
    if(l==r)return;
    int mid=(l+r)/2;
    if(mid>=pos)update(l,mid,T[x].l,T[y].l,pos);
    else update(mid+1,r,T[x].r,T[y].r,pos);
}
int query(int l,int r,int x,int y,int k){
    if(l==r)return l;
    int mid=(l+r)/2;
    int sum=T[T[y].l].sum-T[T[x].l].sum;
    if(sum>=k)return query(l,mid,T[x].l,T[y].l,k);
    else return query(mid+1,r,T[x].r,T[y].r,k-sum);
}
template <class T>
inline bool read(T &ret){
    char c;int sgn;if(c=getchar(),c==EOF)return 0;
    while(c!='-'&&(c<'0'||c>'9'))c=getchar();sgn=(c=='-')?-1:1;ret=(c=='-')?0:(c-'0');
    while(c=getchar(),c>='0'&&c<='9')ret=ret*10+(c-'0');ret*=sgn;return 1;
}
inline void out(int x){if(x>9)out(x/10);putchar(x%10+'0');}
int main()
{
   /* std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);*/
    read(n);read(m);
    for(int i=1;i<=n;i++)read(a[i]),v.push_back(a[i]);
    sort(v.begin(),v.end());v.erase(unique(v.begin(),v.end()),v.end());
    for(int i=1;i<=n;i++)update(1,n,root[i],root[i-1],getid(a[i]));
    while(m--){
       // cin>>x>>y>>k;
       read(x);read(y);read(k);
        out(v[query(1,n,root[x-1],root[y],k)-1]);puts("");
       // cout<<v[query(1,n,root[x-1],root[y],k)-1]<<endl;
    }
    return 0;
}

P2617 Dynamic Rankings (主席树套树状数组)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
struct node{int l,r,sum;}s[maxn*20];
vector<int>v;
struct quest{char op;int x,y,k;}Q[maxn];
inline int get(int x){return lower_bound(v.begin(),v.end(),x)-v.begin()+1;}
inline int lowbit(int x){return x&(-x);}
int a[maxn],b[maxn],T[maxn];
int n,m;
int tot;
int len;
int temp[2][100],cnt[2];
void update(int &now,int l,int r,int pos,int val){
    if(now==0)now=++tot;
    s[now].sum+=val;
    if(l==r)return;
    int mid=(l+r)/2;
    if(pos<=mid)update(s[now].l,l,mid,pos,val);
    else update(s[now].r,mid+1,r,pos,val);
}
void uptree(int x,int val){
    int pos=get(a[x]);
    for(int i=x;i<=n;i+=lowbit(i))update(T[i],1,len,pos,val);
}
int query(int l,int r,int k){
    if(l==r)return l;
    int x=0,mid=(l+r)/2;
    for(int i=1;i<=cnt[1];i++)x+=s[s[temp[1][i]].l].sum;
    for(int i=1;i<=cnt[0];i++)x-=s[s[temp[0][i]].l].sum;
    if(k<=x){
        for(int i=1;i<=cnt[1];i++)temp[1][i]=s[temp[1][i]].l;
        for(int i=1;i<=cnt[0];i++)temp[0][i]=s[temp[0][i]].l;
        return query(l,mid,k);
    }
    else{
        for(int i=1;i<=cnt[1];i++)temp[1][i]=s[temp[1][i]].r;
        for(int i=1;i<=cnt[0];i++)temp[0][i]=s[temp[0][i]].r;
        return query(mid+1,r,k-x);
    }
}
int qutree(int x,int y,int k){
    memset(temp,0,sizeof(temp));
    cnt[0]=cnt[1]=0;
    for(int i=y;i;i-=lowbit(i))temp[1][++cnt[1]]=T[i];
    for(int i=x-1;i;i-=lowbit(i))temp[0][++cnt[0]]=T[i];
    return query(1,len,k);
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>a[i],v.push_back(a[i]);
    for(int i=1;i<=m;i++){
        cin>>Q[i].op>>Q[i].x>>Q[i].y;
        if(Q[i].op=='Q')cin>>Q[i].k;
        else v.push_back(Q[i].y);
    }
    sort(v.begin(),v.end());v.erase(unique(v.begin(),v.end()),v.end());
    len=v.size();
    for(int i=1;i<=n;i++)uptree(i,1);
    for(int i=1;i<=m;i++){
        if(Q[i].op=='Q')cout<<v[qutree(Q[i].x,Q[i].y,Q[i].k)-1]<<endl;
        else{
            uptree(Q[i].x,-1);
            a[Q[i].x]=Q[i].y;
            uptree(Q[i].x,1);
        }
    }
    return 0;
}

P3157 [CQOI2011]动态逆序对 (主席树套树状数组)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
struct node{int l,r,sum;}T[maxn*20];
int a[maxn],p[maxn],c[maxn],uu,pre[maxn],suf[maxn];
int xx[100],yy[100];
int n,m,ooo,rot[maxn];
inline int lowbit(int x){return x&(-x);}
void add(int x,int k){
    for(int i=x;i<=n;i+=lowbit(i))c[i]+=k;
}
int getsum(int x){
    int k=0;
    for(int i=x;i;i-=lowbit(i))k+=c[i];return k;
}
int query(int o,int l,int r,int x,int y){
    if(!o)return 0;
    if(l>=x&&r<=y)return T[o].sum;
    else{
        int mid=(l+r)/2;
        int ans=0;
        if(x<=mid)ans+=query(T[o].l,l,mid,x,y);
        if(mid<y)ans+=query(T[o].r,mid+1,r,x,y);
        return ans;
    }
}
int queryRange(int uu,int vv,int xx,int yy){
    int tmp=0;
    for(int i=uu-1;i;i-=lowbit(i))
        tmp-=query(rot[i],1,n,xx,yy);
    for(int i=vv;i;i-=lowbit(i))
        tmp+=query(rot[i],1,n,xx,yy);
    return tmp;
}
void update(int &rt,int l,int r,int x){
    if(!rt)rt=++ooo;
    T[rt].sum++;
    if(l==r)return;
    int mid=(l+r)/2;
    if(x<=mid)update(T[rt].l,l,mid,x);
    if(mid<x)update(T[rt].r,mid+1,r,x);
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    cin>>n>>m;
    ll ans=0;
    for(int i=1;i<=n;i++){
        cin>>a[i];
        p[a[i]]=i;
        pre[i]=getsum(n)-getsum(a[i]);
        ans+=pre[i];
        add(a[i],1);
    }
    memset(c,0,sizeof(c));
    for(int i=n;i>=1;i--){
        suf[i]=getsum(a[i]-1);
        add(a[i],1);
    }
    while(m--){
        cout<<ans<<endl;
        cin>>uu;
        uu=p[uu];
        ans-=pre[uu]+suf[uu];
        ans+=queryRange(1,uu-1,a[uu]+1,n);
        ans+=queryRange(uu+1,n,1,a[uu]-1);
        for(int i=uu;i<=n;i+=lowbit(i))
            update(rot[i],1,n,a[uu]);
    }
    return 0;
}

洛谷试炼场 3-5数论 3-17 倍增

Diposting di 2019-04-24 | Edited on 2019-02-07

P2152 [SDOI2009]SuperGCD

思路

直接上python

a=int(input())
b=int(input())
while a!=0:
    b%=a
    k=a
    a=b
    b=k
print(b)

P1414 又是毕业季II

思路

把每个数sqrt时间分解因子，然后枚举因子个数

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int a[maxn];
int num[maxn];
int mx[maxn];
void solve(int x){
    for(int i=1;i<=sqrt(x);i++){
        if(x%i==0){
            a[i]++;
            if(i*i!=x)a[x/i]++;
        }
    }
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n;
    cin>>n;
    int mp=0;
    for(int i=1;i<=n;i++){
        int aa;
        cin>>aa;
        solve(aa);
        mp=max(mp,aa);
    }
    for(int i=1;i<=n;i++){
        while(a[mp]<i)mp--;
        cout<<mp<<endl;
    }
    return 0;
}

P1313 计算系数

思路

直接递推

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=10007;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
ll dp[1100][1100];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int a,b,k,n,m;
    cin>>a>>b>>k>>n>>m;
    dp[0][0]=1;
    for(int i=0;i<=n;i++)
    for(int j=0;j<=m;j++){
       if(i)dp[i][j]=(dp[i][j]+dp[i-1][j]*a)%mod;
       if(j)dp[i][j]=(dp[i][j]+dp[i][j-1]*b)%mod;
    }
    cout<<dp[n][m]<<endl;
    return 0;
}

P1306 斐波那契公约数 (gcd(Fn,Fm)=F(gcd(n,m)))

思路

只要知道gcd(fn,fm)=F（gcd(n,m))然后用一下矩阵快速幂就行

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e8;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;

typedef vector<ll>vec;
typedef vector<vec>mat;
mat mul(mat& A,mat &B){
    mat C(A.size(),vec(B[0].size()));
    for(int i=0;i<A.size();i++)
        for(int k=0;k<B.size();k++)
        if(A[i][k])
            for(int j=0;j<B[0].size();j++)
            C[i][j]=(C[i][j]+A[i][k]*B[k][j]%mod+mod)%mod;
    return C;
}
mat Pow(mat A,ll n){
    mat B(A.size(),vec(A.size()));
    for(int i=0;i<A.size();i++)B[i][i]=1;
    for(;n;n>>=1,A=mul(A,A))
        if(n&1)B=mul(B,A);
    return B;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    ll n,m;
    cin>>n>>m;
    n=__gcd(n,m);
    if(n==1){
        cout<<1<<endl;return 0;
    }
    mat solve(2,vec(2));
    solve[0][0]=1;solve[0][1]=1;
    solve[1][0]=1;solve[1][1]=0;
    mat ex(2,vec(1));
    ex[0][0]=1;ex[1][0]=1;
    solve=Pow(solve,n-2);
    solve=mul(solve,ex);
    cout<<solve[0][0]<<endl;
    return 0;
}

P1967 货车运输（最大生成树+LCA）

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e8;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int n,m;
struct Edge{
    int from,to,w;
    bool operator <(const Edge a)const{
        return this->w>a.w;
    }
};
vector<Edge>edges;
int f[maxn];
vector<Edge>ve[maxn];
int find(int x){
    return f[x]==x?f[x]:(f[x]=find(f[x]));
}
void unite(int a,int b){
    int aa=find(a),bb=find(b);
    if(aa>bb)f[aa]=bb;
    else f[bb]=f[aa];
}
void kruskal(){
    for(int i=0;i<=n;i++)f[i]=i;
    for(int i=0;i<2*m;i++){
        if(find(edges[i].from)!=find(edges[i].to)){
            unite(edges[i].from,edges[i].to);
            ve[edges[i].from].push_back(Edge{0,edges[i].to,edges[i].w});
            ve[edges[i].to].push_back(Edge{0,edges[i].from,edges[i].w});
        }
    }
}
int mi[maxn][22],fa[maxn][22],dep[maxn];
void dfs(int now,int pre,int w,int deep){
    fa[now][0]=pre;
    mi[now][0]=w;
    if(pre==0)mi[now][0]=inf,fa[now][0]=now;
    dep[now]=deep;
    for(auto i:ve[now]){
        if(i.to==pre)continue;
        dfs(i.to,now,i.w,deep+1);
    }
}
void init(){
    for(int i=1;i<=20;i++)
    for(int j=1;j<=n;j++){
        int p=fa[j][i-1];
        fa[j][i]=fa[p][i-1];
        mi[j][i]=min(mi[j][i-1],mi[p][i-1]);
    }
}
int lca(int p,int q){
    if(dep[p]<dep[q])swap(p,q);
    int res=inf;
    for(int i=20;i>=0;i--)
        if(dep[fa[p][i]]>=dep[q])
        res=min(res,mi[p][i]),p=fa[p][i];
    if(p==q)return res;
    for(int i=20;i>=0;i--){
        if(fa[p][i]!=fa[q][i]){
            res=min(res,mi[p][i]);
            res=min(res,mi[q][i]);
            p=fa[p][i];q=fa[q][i];
        }
    }
    return min(res,min(mi[p][0],mi[q][0]));
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    cin>>n>>m;
    for(int i=1;i<=m;i++){
        int a,b,c;
        cin>>a>>b>>c;
        edges.push_back(Edge{a,b,c});
        edges.push_back(Edge{b,a,c});
    }
    sort(edges.begin(),edges.end());
    kruskal();
    for(int i=1;i<=n;i++){
        if(f[i]==i){
            dfs(i,0,0,0);
        }
    }
    init();
    int q;cin>>q;
    while(q--){
        int x,y;
        cin>>x>>y;
        if(find(x)!=find(y))cout<<-1<<endl;
        else cout<<lca(x,y)<<endl;
    }
    return 0;
}

P1613 跑路（倍增+floyd）

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int d[100][100],n,m;
bool ok[100][100][100];

int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    memset(d,inf,sizeof(d));
    cin>>n>>m;
    while(m--){
        int x,y;
        cin>>x>>y;
        d[x][y]=1;
        ok[x][y][0]=true;
    }
    for(int log=1;log<=50;log++)
        for(int k=1;k<=n;k++)
        for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
    if(ok[i][k][log-1]&&ok[k][j][log-1]){
        ok[i][j][log]=true;
        d[i][j]=1;
    }
    for(int k=1;k<=n;k++)
    for(int i=1;i<=n;i++)
    for(int j=1;j<=n;j++)
    if(d[i][j]>(d[i][k]+d[k][j])){
        d[i][j]=d[i][k]+d[k][j];
    }
    cout<<d[1][n]<<endl;
    return 0;
}

洛谷试炼场 2-7，2-8，2-9

Diposting di 2019-04-24 | Edited on 2019-02-06

DFS

八皇后

思路

只要把对角线的规律找出来就OK

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int ans=0;
int h[1050],w[1050],le[1050],re[1050];
int n;
void print(){
    ans++;
    if(ans<=3){
        for(int i=1;i<=n;i++){
            if(i!=1)cout<<" ";
            cout<<h[i];
        }
        cout<<endl;
    }
}
void dfs(int id){
    if(id>n){print();return;}
    for(int i=1;i<=n;i++){
        if(w[i]==0&&le[i+id]==0&&re[i-id+100]==0){
            w[i]=1;
            h[id]=i;
            le[i+id]=1;
            re[i-id+100]=1;
            dfs(id+1);
            w[i]=0;
            h[id]=0;
            le[i+id]=0;
            re[i-id+100]=0;
        }
    }
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    cin>>n;
    dfs(1);
    cout<<ans<<endl;
    return 0;
}

单词方阵

思路

找出第一个字符然后八个方向直线过去就行

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int dx[8]={1,-1,0,0,1,1,-1,-1};
int dy[8]={0,0,-1,1,1,-1,1,-1};
char ok[100]={'y','i','z','h','o','n','g'};
char s[150][150];
char ans[150][150];
int n;
bool check(int x,int y){
    if(x<=n&&y<=n&&x>=1&&y>=1)return true;
    else return false;
}
bool dfs(int x,int y,int id,int p){
    if(id==6){ans[x][y]=ok[id];return true;}
    int f=0;
    for(int i=p;i<=p;i++){
        int xx=x+dx[i],yy=y+dy[i];
        if(check(xx,yy)&&s[xx][yy]==ok[id+1]){
            if(dfs(xx,yy,id+1,p))ans[x][y]=ok[id],f=1;
        }
    }
    if(f==1)return true;
    else return false;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>s[i]+1;
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            if(s[i][j]=='y'){
                for(int p=0;p<8;p++)
                dfs(i,j,0,p);
            }
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            if(ans[i][j])cout<<ans[i][j];
            else cout<<'*';
        }
        cout<<endl;
    }
    return 0;
}

迷宫

比较水的题

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int dx[8]={1,-1,0,0,1,1,-1,-1};
int dy[8]={0,0,-1,1,1,-1,1,-1};
int n,m;
int mp[150][150];
int ans=0;
int sx,sy,ex,ey;
int vis[150][150];
bool check(int x,int y){
    if(x<=n&&y<=m&&x>=1&&y>=1)return true;
    else return false;
}
void dfs(int x,int y){
    if(x==ex&&y==ey){
        ans++;return;
    }
    vis[x][y]=1;
    for(int i=0;i<4;i++){
        int xx=x+dx[i],yy=y+dy[i];
        if(check(xx,yy)&&mp[xx][yy]==0&&vis[xx][yy]==0){
            dfs(xx,yy);
        }
    }
    vis[x][y]=0;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int t;
    cin>>n>>m;
    cin>>t;
    cin>>sx>>sy>>ex>>ey;
    for(int i=1;i<=t;i++){
        int a,b;
        cin>>a>>b;
        mp[a][b]=1;
    }
    dfs(sx,sy);cout<<ans<<endl;
    return 0;
}

BFS

填图颜色

思路

把周围的0都涂完剩下的就是答案

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int dx[8]={1,-1,0,0,1,1,-1,-1};
int dy[8]={0,0,-1,1,1,-1,1,-1};
int n,m;
int mp[150][150];
struct node{
    int x,y;
};
bool check(int x,int y){
    if(x<=n&&y<=n&&x>=1&&y>=1&&mp[x][y]==0)return true;
    else return false;
}
void bfs(int x,int y){
    queue<node>Q;
    Q.push(node{x,y});
    mp[x][y]=2;
    while(!Q.empty()){
        node now=Q.front();Q.pop();
        for(int i=0;i<4;i++){
            int xx=now.x+dx[i];
            int yy=now.y+dy[i];
            if(check(xx,yy)){
                mp[xx][yy]=2;
                Q.push(node{xx,yy});
            }
        }
    }
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    cin>>n;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            cin>>mp[i][j];
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            if((i==1||j==1||i==n||j==n)&&(mp[i][j]==0)){
                bfs(i,j);
            }
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            if(mp[i][j]==0)cout<<"2";
            else if(mp[i][j]==1)cout<<"1";
            else if(mp[i][j]==2)cout<<"0";
            if(j==n)cout<<endl;
            else cout<<" ";
        }
    }
    return 0;
}

01迷宫(联通块加速)

思路

格子太大查询太多直接暴力会超时，所以采用联通快加速

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int dx[8]={1,-1,0,0,1,1,-1,-1};
int dy[8]={0,0,-1,1,1,-1,1,-1};
int n,m;
char mp[1100][1100];
int fa[1100*1100+50];
int value[1100*1100+50];
bool vis[1100][1100];
struct node{
    int x,y;
    char id;
};
bool check(int x,int y,char id){
    if(x<n&&y<n&&x>=0&&y>=0&&(id!=mp[x][y]))return true;
    else return false;
}
int find(int x){
    return x==fa[x]?x:fa[x]=find(fa[x]);
}
void unite(int a,int b){
    int aa=find(a),bb=find(b);
    if(aa==bb)return;
    if(aa<bb){
        fa[bb]=aa;
        value[aa]+=value[bb];
    }
    else fa[aa]=bb,value[bb]+=value[aa];
}
inline int ID(int x,int y){return x*n+y;};
void bfs(int x,int y){
    queue<node>Q;
    Q.push(node{x,y,mp[x][y]});
    vis[x][y]=1;
    while(!Q.empty()){
        node now=Q.front();Q.pop();
        for(int i=0;i<4;i++){
            int xx=now.x+dx[i];
            int yy=now.y+dy[i];
            if(check(xx,yy,now.id)&&vis[xx][yy]==false){
                unite(ID(x,y),ID(xx,yy));
                vis[xx][yy]=1;
                Q.push(node{xx,yy,mp[xx][yy]});
            }
        }
    }
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    cin>>n>>m;
    for(int i=0;i<n;i++)cin>>mp[i];
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++){
            fa[i*n+j]=i*n+j;
            value[i*n+j]=1;
        }
    }
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++){
            if(!vis[i][j])bfs(i,j);
        }
    }
    while(m--){
        int a,b;
        cin>>a>>b;
        cout<<value[find(ID(a-1,b-1))]<<endl;
    }
    return 0;
}

马的遍历（水）

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int dx[8]={1,1,-1,-1,2,2,-2,-2};
int dy[8]={2,-2,2,-2,1,-1,1,-1};
int n,m;
bool vis[1100][1100];
int ans[450][450];
struct node{
    int x,y,step;
};
bool check(int x,int y){
    if(x<=n&&y<=m&&x>=1&&y>=1&&vis[x][y]==false)return true;
    else return false;
}
void bfs(int x,int y){
    queue<node>Q;
    Q.push(node{x,y,0});
    vis[x][y]=1;
    while(!Q.empty()){
        node now=Q.front();Q.pop();
        ans[now.x][now.y]=now.step;
        for(int i=0;i<8;i++){
            int xx=now.x+dx[i];
            int yy=now.y+dy[i];
            if(check(xx,yy)){
                vis[xx][yy]=1;
                Q.push(node{xx,yy,now.step+1});
            }
        }
    }
}
int main()
{
   // std::ios::sync_with_stdio(false);
   // std::cin.tie(0);
   // std::cout.tie(0);
    memset(ans,-1,sizeof(ans));
    int sx,sy;
    cin>>n>>m;
    cin>>sx>>sy;
    bfs(sx,sy);
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
        printf("%-5d",ans[i][j]);
        }cout<<endl;
    }
    return 0;
}

带有技巧的搜索

线性基学习笔记

Diposting di 2019-04-24 | Edited on 2018-09-30

总结

线性基的题型相对比较固定，看到下面的类型基本上都是线性基了：

最大异或和
第 k 大异或和/异或和是第几大
求所有异或值的和

线性基中的题目中还用到一个技巧：

任意一条 1到 n 的路径的异或和，都可以由任意一条 1 到 n 路径的异或和与图中的一些环的异或和来组合得到。

这便是线性基的全部东西了。

模板

struct Linear_Basis{
	long long d[65],p[65];
	int cnt;
	Linear_Basis(){
		memset(d,0,sizeof(d));
		memset(p,0,sizeof(p));
		cnt=0;
	}

	bool ins(long long val){
		for (int i=62;i>=0;i--) {
			if (val&(1LL<<i)){
				if (!d[i]){
					d[i]=val;
					break;
				}
				val^=d[i];
			}
		}
		return val>0;
	}

	long long query_max(long long D=0LL){
		long long ret=D;
		for (int i=62;i>=0;i--)
			if ((ret^d[i])>ret) ret^=d[i];
		return ret;
	}

    long long query_min(long long D=0LL){
        long long ret=D;
        for(int i=0;i<=62;i++){
            if(d[i]) ret^=d[i];
        }
        return ret;
    }

	void rebuild(){
		for (int i=1;i<=62;i++)
			for (int j=0;j<i;j++)
				if (d[i]&(1LL<<j)) d[i]^=d[j];
		cnt=0;
		for (int i=0;i<=62;i++)
			if (d[i]) p[cnt++]=d[i];
	}
    //第K大
	long long kthquery(long long k){
		long long ret=0;
		if (k>=(1LL<<cnt)) return -1;
		for (int i=0;i<=62;i++)
			if (k&(1LL<<i)) ret^=p[i];
		return ret;
	}
	Linear_Basis merge(const Linear_Basis &n1,const Linear_Basis &n2){
	    Linear_Basis ret=n1;
	    for(int i=62;i>=0;i--)
            if(n2.d[i])ret.ins(n2.d[i]);
        return ret;
	}
};

A.BZOJ-2460 [BeiJing2011]元素

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int inf=0x3f3f3f3f;
const int maxn=1e5+50;
//线性基
struct Linear_Basis{
	long long d[65],p[65];
	int cnt;
	Linear_Basis(){
		memset(d,0,sizeof(d));
		memset(p,0,sizeof(p));
		cnt=0;
	}

	bool ins(long long val){
		for (int i=62;i>=0;i--) {
			if (val&(1LL<<i)){
				if (!d[i]){
					d[i]=val;
					break;
				}
				val^=d[i];
			}
		}
		return val>0;
	}

	long long query_max(long long D=0LL){
		long long ret=D;
		for (int i=62;i>=0;i--)
			if ((ret^d[i])>ret) ret^=d[i];
		return ret;
	}

    long long query_min(long long D=0LL){
        long long ret=D;
        for(int i=0;i<=62;i++){
            if(d[i]) ret^=d[i];
        }
        return ret;
    }

	void rebuild(){
		for (int i=1;i<=62;i++)
			for (int j=0;j<i;j++)
				if (d[i]&(1LL<<j)) d[i]^=d[j];
		cnt=0;
		for (int i=0;i<=62;i++)
			if (d[i]) p[cnt++]=d[i];
	}
    //第K大
	long long kthquery(long long k){
		long long ret=0;
		if (k>=(1LL<<cnt)) return -1;
		for (int i=0;i<=62;i++)
			if (k&(1LL<<i)) ret^=p[i];
		return ret;
	}
};
struct node{
    ll a,b;
    bool operator <(node a)const{
        return this->b>a.b;
    }
}my[1100];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n;
    Linear_Basis LB=Linear_Basis();
    cin>>n;
    for(int i=0;i<n;i++){
        cin>>my[i].a>>my[i].b;
    }
    sort(my,my+n);
    ll ans=0;
    for(int i=0;i<n;i++){
        if(LB.ins(my[i].a))ans+=my[i].b;
    }
    cout<<ans<<endl;
    return 0;
}

「kuangbin带你飞」专题二十二区间DP

Diposting di 2019-04-24 | Edited on 2018-09-25

传送门

B.LightOJ - 1422 Halloween Costumes

题意

按顺序参加舞会，参加一个舞会要穿一种衣服，可以在参加完一个舞会后套上另一个衣服再去参加舞会，也可以在参加一个舞会的时候把外面的衣服脱了，脱到合适的衣服，但是脱掉的衣服不能再穿，参加完全部舞会最少穿多少次衣服

题解

区间dp，dp【i】【j】表示区间i->j之间的衣服数起始情况i->i要穿一件衣服

可以从后往前推

$dp[i][j]=dp[i+1][j]+1$

特别的如果第i 和第j个衣服是一样的

$dp[i][j]=dp[i][j-1]$

然后开始在区间{I,J}之间选择K；

如果K的衣服和I的衣服一样代表到K的时候可以把衣服脱到剩I的时候这样就是K前面的衣服加上K->J的衣服

$dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j])$

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
int dp[110][110];
int a[110];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int t;
    cin>>t;
    int cnt=1;
    while(t--){
        int n;
        cin>>n;
        memset(dp,0,sizeof(dp));
        for(int i=1;i<=n;i++)cin>>a[i],dp[i][i]=1;
        for(int i=n-1;i>=1;i--){
            for(int j=i+1;j<=n;j++){
                dp[i][j]=dp[i+1][j]+1;
                if(a[i]==a[j])dp[i][j]=dp[i][j-1];
                for(int k=i+1;k<j;k++){
                    if(a[i]==a[k]){
                        dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]);
                       // cout<<"i=="<<i<<"   j=="<<" dp[i][j]="<<dp[i][j]<<endl;
                    }
                }
            }
        }
        cout<<"Case "<<cnt++<<": ";
        cout<<dp[1][n]<<endl;
    }
    return 0;
}

C.POJ - 2955 Brackets

题意

给出一个的只有’(‘,’)’,’[‘,’]’四种括号组成的字符串，求最多有多少个括号满足题目里所描述的完全匹配。

题解

用dp[i][j]表示区间[i,j]里最大完全匹配数。
只要得到了dp[i][j]，那么就可以得到dp【i-1][j+1]
dp【i-1]【j+1]=dp 【i]【j]+(s[i-1]与[j+1]匹配 ? 2 : 0)
然后利用状态转移方程更新一下区间最优解即可。

$dp[i][j]=max(dp[i][j],dp[i][k]+dp[k+1][j])$

#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=998244353;
const int maxn=1e3+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
char s[maxn];
int dp[maxn][maxn];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    while(cin>>s+1){
        if(s[1]=='e')break;
        memset(dp,0,sizeof(dp));
        int n=strlen(s+1);
        for(int len=2;len<=n;len++)
        for(int i=1;i<=n;i++){
            int j=i+len-1;
            if(j>n)break;
            if(s[i]=='('&&s[j]==')'||s[i]=='['&&s[j]==']'){
                dp[i][j]=dp[i+1][j-1]+2;
            }
            for(int k=i;k<j;k++){
                dp[i][j]=max(dp[i][j],dp[i][k]+dp[k][j]);
            }
        }
        cout<<dp[1][n]<<endl;
    }
    return 0;
}

D.CodeForces - 149D Coloring Brackets

题意

给你一个只有括号的字符串，

1,每个括号只有三种选择：涂红色，涂蓝色，不涂色。

2,每对括号有且仅有其中一个被涂色。

3,相邻的括号不能涂相同的颜色，但是相邻的括号可以同时不涂色。

题解

因为是一个合法的括号序列。

所以每个括号与之匹配的位置是一定的。

那么就可以将这个序列分成两个区间。 (L - match[L] ) (match[L]+1, R)

用递归先处理小区间，再转移大区间。

因为条件的限制，所以记录区间的同时，还要记录区间端点的颜色。

然后就是一个递归的过程。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=1e9+7;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
ll dp[800][800][3][3];
int a[110];
ll ans;
char s[800];
int match[800];
int stk[800];
void dfs(int l,int r){
    if(l+1==r){
        dp[l][r][0][1]=dp[l][r][0][2]=dp[l][r][1][0]=dp[l][r][2][0]=1;
        return;
    }
    if(match[l]==r){
        dfs(l+1,r-1);
        for(int i=0;i<3;i++){
            for(int j=0;j<3;j++){
                if(j!=1)dp[l][r][0][1]=(dp[l][r][0][1]+dp[l+1][r-1][i][j])%mod;
                if(j!=2)dp[l][r][0][2]=(dp[l][r][0][2]+dp[l+1][r-1][i][j])%mod;
                if(i!=1)dp[l][r][1][0]=(dp[l][r][1][0]+dp[l+1][r-1][i][j])%mod;
                if(i!=2)dp[l][r][2][0]=(dp[l][r][2][0]+dp[l+1][r-1][i][j])%mod;
            }
        }
    }
    else{
        dfs(l,match[l]);
        dfs(match[l]+1,r);
        for(int i=0;i<3;i++){
            for(int j=0;j<3;j++){
                for(int k=0;k<3;k++){
                    for(int p=0;p<3;p++){
                        if(j&&j==k)continue;
                        dp[l][r][i][p]=(dp[l][r][i][p]+(dp[l][match[l]][i][j]*dp[match[l]+1][r][k][p]%mod)%mod)%mod;
                    }
                }
            }
        }
    }
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int t;
    int cnt=1;
    cin>>s+1;
    int n=strlen(s+1);
    memset(match,0,sizeof(match));
    int top=-1;
    for(int i=1;i<=n;i++){
        if(s[i]=='(')stk[++top]=i;
        else match[stk[top--]]=i;
    }
    memset(dp,0,sizeof(dp));
    dfs(1,n);
    ans=0;
    for(int i=0;i<3;i++)
    for(int j=0;j<3;j++){
        ans=(ans+dp[1][n][i][j])%mod;
    }
    cout<<ans<<endl;
    return 0;
}

E.POJ - 1651 Multiplication Puzzle

题意

给出N个数，每次从中抽出一个数(第一和最后一个不能抽)，每次的得分为抽出的数与相邻两个数的乘积，直到只剩下首尾两个数为止，问最小得分是多少

题解1

枚举起点和终点 ,但是这次长度要从3开始了因为中间必要取一个

#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=998244353;
const int maxn=1e2+50;
const int inf=0x3f3f3f3f;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
int a[maxn];
int dp[maxn][maxn];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n;
    while(cin>>n){
        for(int i=1;i<=n;i++)cin>>a[i];
        memset(dp,0,sizeof(dp));

        for(int len=3;len<=n;len++){
            for(int i=1;i<=n;i++){
                int j=i+len-1;
                if(j>n)continue;
                dp[i][j]=inf;
                for(int k=i+1;k<j;k++){
                    dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]+a[i]*a[j]*a[k]);
                    //cout<<"i=="<<i<<"   j="<<j<<"   k=="<<k<<"   dp[i][j]="<<dp[i][j]<<endl;
                }
            }
        }
        cout<<dp[1][n]<<endl;
    }
    return 0;
}

题解2

记忆化搜索

#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=998244353;
const int maxn=1e2+50;
const int inf=0x3f3f3f3f;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
int a[maxn];
int dp[maxn][maxn];
int dfs(int s,int t){
    if(dp[s][t]!=-1)return dp[s][t];
    if(t-s<=1)return 0;
    int ans=inf;
    for(int i=s+1;i<t;i++)
        ans=min(ans,dfs(s,i)+dfs(i,t)+a[s]*a[t]*a[i]);
    dp[s][t]=ans;
    return ans;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n;
    while(cin>>n){
        for(int i=1;i<=n;i++)cin>>a[i];
        memset(dp,-1,sizeof(dp));
        cout<<dfs(1,n)<<endl;
    }
    return 0;
}

G.HDU - 4283 You Are the One

题意

有一个队列，每个人有一个愤怒值D，如果他是第K个上场，不开心指数就为(K-1)*D。但是边上有一个小黑屋（其实就是个堆栈），可以一定程度上调整上场程序

题意

对于区间 [x, y] 中的数字 a[x]，有可能第1个出栈，也有可能最后一个出栈，如果第k个出栈的话前i+1->k个数字要按照顺序出栈，然后a[x]出栈，[k+1,y]出栈。对于a[x]要加上a[x]×(k-i）的花费，对于[x+1, y]要加上sum(x+1, y) * (i-x+1)的额外花费。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
int dp[110][110];
int a[110];
int ans[110];
int sum[110];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int t;
    int cnt=1;
    cin>>t;
    while(t--){
        int n;
        cin>>n;
        memset(dp,0,sizeof(dp));
        memset(sum,0,sizeof(sum));
        for(int i=1;i<=n;i++)cin>>a[i],dp[i][i]=0,sum[i]=sum[i-1]+a[i];
        for(int len=2;len<=n;len++)
        for(int i=1;i<=n;i++){
            int j=i+len-1;
            if(j>n)break;
            dp[i][j]=inf;
            for(int k=i;k<=j;k++){
                dp[i][j]=min(dp[i][j],a[i]*(k-i)+(k-i+1)*(sum[j]-sum[k])+dp[i+1][k]+dp[k+1][j]);
            }
        }
        cout<<"Case #"<<cnt++<<": ";
        cout<<dp[1][n]<<endl;
    }
    return 0;
}

H.HDU - 2476 String painter

题意

给出两个长度相同的字符串a, b.对a可以进行区间更新(选择一个区间，把这个区间全部更新成相同的字符)，问要最少操作a多少次，a才能等于b？

题解

先处理一下b串用DP存b串i到j的改变次数然后再对a串进行状态转移。对于串b，最要是看两个相同字符之间的区间了。我们可以预处理出来改变区间[x, y]里面的字符，操作的最小次数用dp[x, y]来存储。
　　预处理完了以后，我们就可以用dp来匹配a了。ans[i] 表示 a字符区间[0, i] 与 b字符区间[0, i]相同的最小操作数目。状态转移就是：ans[i] = min (dp[0, i], ans[j] + dp【j+1】i], ans【i-1)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
int dp[110][110];
char a[110],b[110];
int ans[110];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    while(cin>>a>>b){
        memset(dp,0,sizeof(dp));
        int n=strlen(b);
        for(int i=0;i<n;i++)dp[i][i]=1;
        for(int len=2;len<=n;len++)
        for(int i=0;i<n;i++){
            int j=i+len-1;
            if(j>=n)break;
            if(b[i]==b[j])dp[i][j]=dp[i+1][j];
            else
                dp[i][j]=dp[i+1][j]+1;
            for(int k=i+1;k<j;k++){
                if(b[k]==b[i])
                    dp[i][j]=min(dp[i][j],dp[i+1][k]+dp[k+1][j]);
            }
        }
        ans[0]=a[0]==b[0]?0:1;
        for(int i=1;i<n;i++){
            ans[i]=dp[0][i];
            if(a[i]==b[i])ans[i]=min(ans[i],ans[i-1]);
            for(int j=0;j<i;j++)
                ans[i]=min(ans[i],ans[j]+dp[j+1][i]);
        }
        cout<<ans[n-1]<<endl;
    }
    return 0;
}

「kuangbin带你飞」专题二十斜率DP

Diposting di 2019-04-24 | Edited on 2018-09-26

传送门

A.HDU - 3507 Print Article

题意

就是输出序列a[n]，每连续输出的费用是连续输出的数字和的平方加上常数M

让我们求这个费用的最小值。

题解

概率DP的入门题，把我搞得要死要活的。

首先dp[i]表示输出前i个的最小费用很简单得得出一个方程

$dp[i]=min(dp[i],dp[j]+(sum[i]-sum[j])^2\\1<=j<i$

其中sum[i]表示数字的前i项和，但是这个方程的复杂度是n^2 所以这时候就要用到斜率优化，ps：个人感觉斜率DP都用到了队列，来把前面绝对不优秀的项都出队，这样每次运算都只要在队列中找就行，而且每个元素只有一次出队和入队所以复杂度只有N

首先假设在算dp[i]的，k<j<i，并且J点比K点优秀

那么

$dp[j]+(sum[i]-sum[j])^2+M<=dp[k]+(sum[i]-sum[k])^2+M$

对上面方程分解整理得：

$[(dp[j]+sum[j]^2)-(dp[k]+sum[k]^2)]÷2(sum[j]-sum[k])<=sum[i]$

注意正负号，不然会影响不等号的方向

另

$Y(x)=dp[x]+sum[j]^2\\X(x)=2×sum[j]$

于是上面的式子变成斜率表达式

$[Y(j)-Y(k)]/[X(j)-X(k)]<=sum[i]$

由于不等式右边的sum[i]随着i的增加而递增

所以我们另

$g[j,k]=[Y(j)-Y(k)]/[X(j)-X(k)]$

1.如果上面的不等式成立说明J比K优,而且随着i的增加上述不等式一定是成立的，也就是对于以后的i来说J都比K优秀，所以K是可以淘汰的

2.如果

$g[J，K]>g[I，J]\\k<j<i$

那么J是可以淘汰的

假设g[I,J]<sum[i] 就是I比J优秀,那么J就没存在的价值

相反，如果g[I，J]>sum[i] 那么同样有g[J，K]>sum[I] 那么K比J优秀所以J是可以淘汰的

所以这样相当于维护一个下凸的图形，斜率在增加，用队列维护

ps：以上都是抄bin巨的博客

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=998244353;
const int maxn=5e5+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
int dp[maxn];
int sum[maxn];
int a[maxn];
int q[maxn];
int m,n;
int head,tail;
int getDP(int i,int j){
    return dp[j]+m+(sum[i]-sum[j])*(sum[i]-sum[j]);
}
int getUP(int j,int k){
    return dp[j]+sum[j]*sum[j]-(dp[k]+sum[k]*sum[k]);
}
int getDOWN(int j,int k){
    return 2*(sum[j]-sum[k]);
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    while(cin>>n>>m){
        for(int i=1;i<=n;i++)cin>>a[i];
        memset(sum,0,sizeof(sum));
        memset(dp,0,sizeof(dp));
        for(int i=1;i<=n;i++)sum[i]=sum[i-1]+a[i];
        head=tail=0;
        q[tail++]=0;
        for(int i=1;i<=n;i++){
            while(head+1<tail&&getUP(q[head+1],q[head])<=sum[i]*getDOWN(q[head+1],q[head]))
                head++;
            dp[i]=getDP(i,q[head]);
            while(head+1<tail&&getUP(i,q[tail-1])*getDOWN(q[tail-1],q[tail-2])<=getUP(q[tail-1],q[tail-2])*getDOWN(i,q[tail-1]))
                tail--;
            q[tail++]=i;
        }
        cout<<dp[n]<<endl;
    }
    return 0;
}

「kuangbin带你飞」专题十九矩阵

Diposting di 2019-04-24 | Edited on 2018-10-06

传送门

A.CodeForces - 450B Jzzhu and Sequences

题意

水题，主要是拿来试试模板

题解

F[i]=f[i-1]-f[i-2]

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define pp pair<int,int>
const ll mod=1e9+7;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
struct Matrix{
    ll mat[5][5];
    int n;
    Matrix(){}
    Matrix(int _n){
        n=_n;
        for(int i=0;i<n;i++)
            for(int j=0;j<n;j++)
            mat[i][j]=0;
    }
    Matrix operator *(const Matrix &b)const{
        Matrix ret=Matrix(n);
        for(int i=0;i<n;i++){
            for(int k=0;k<n;k++){
                if(mat[i][k])
                for(int j=0;j<n;j++){
                    ret.mat[i][j]+=(mat[i][k]*b.mat[k][j]+mod)%mod;
                    ret.mat[i][j]+=mod;
                    ret.mat[i][j]%=mod;
                }
            }
        }
        return ret;
    }
    ull pow_m(ull a,int n){
        ull ret=1,tmp=a;
        while(n){
            if(n&1)ret*=tmp;
            tmp*=tmp;
            n>>=1;
        }
        return ret;
    }
    Matrix pow_M(Matrix a,ll n){
        Matrix ret=Matrix(a.n);
        for(int i=0;i<a.n;i++)ret.mat[i][i]=1;
        Matrix tmp=a;
        while(n){
            if(n&1)ret=ret*tmp;
            tmp=tmp*tmp;
            n>>=1;
        }
        return ret;
    }
};
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    ll x,y,n;
    cin>>x>>y>>n;
    Matrix a=Matrix(2);
    a.mat[0][0]=1;a.mat[0][1]=-1;
    a.mat[1][0]=1,a.mat[1][1]=0;
    if(n==1){cout<<(x+mod)%mod<<endl;return 0;}
    if(n==2){cout<<(y+mod)%mod<<endl;return 0;}
    a=a.pow_M(a,n-2);
    cout<<((a.mat[0][0]*y+a.mat[0][1]*x)%mod+mod)%mod;
    return 0;
}

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=1e9+7;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
ll x,y;
typedef vector<ll>vec;
typedef vector<vec>mat;
mat mul(mat& A,mat &B){
    mat C(A.size(),vec(B[0].size()));
    for(int i=0;i<A.size();i++)
        for(int k=0;k<B.size();k++)
        if(A[i][k])
            for(int j=0;j<B[0].size();j++)
            C[i][j]=(C[i][j]+A[i][k]*B[k][j]%mod+mod)%mod;
    return C;
}
mat Pow(mat A,ll n){
    mat B(A.size(),vec(A.size()));
    for(int i=0;i<A.size();i++)B[i][i]=1;
    for(;n;n>>=1,A=mul(A,A))
        if(n&1)B=mul(B,A);
    return B;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    cin>>x>>y;
    ll n;
    cin>>n;
    if(n==1){
        cout<<(x+mod)%mod<<endl;return 0;
    }
    else if(n==2){
        cout<<(y+mod)%mod<<endl;return 0;
    }
    mat a(2,vec(2));
    a[0][0]=1;a[0][1]=-1;a[1][0]=1;a[1][1]=0;
    a=Pow(a,n-2);
    cout<<(a[0][0]*y%mod+a[0][1]*x%mod+mod+mod)%mod<<endl;
    return 0;
}

B.HDU - 5015 233 Matrix

题意

给出矩阵的第0行（0,233,2333,23333,…）和第0列a1,a2,…an（n<=10，m<=10^9），给出式子：

$A[i][j]=A[i-1][j]+A[i][j-1]$

题解

假设要求A[a]【b]则

$A[a][b]=A[a-1][b]+A[a][b-1]\\=A[a][b-1]+A[a-1][b-1]+A[a-2][b]\\...$

相当于上图，红色部分为绿色部分之和，而顶上的绿色部分很好求左边的部分就是前一列的（1-n)的和

所以我们只要知道第一列和第一行就能推出任意列@

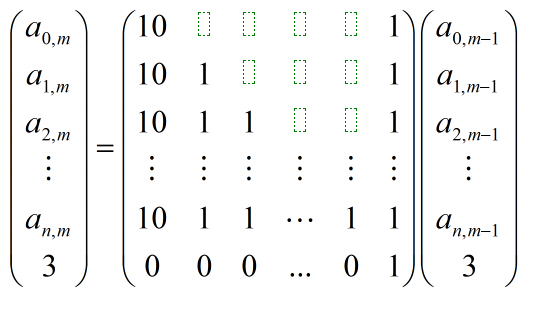
构造上图的中间矩阵，因为第0列到第一列不符合所以手动求出第一列的答案，然后再求出中间矩阵的m-1次方和第一列相乘就是答案了

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define pp pair<int,int>
const ll mod=1e7+7;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
struct Matrix{
    ll mat[15][15];
    int n;
    Matrix(){}
    Matrix(int _n){
        n=_n;
        for(int i=0;i<n;i++)
            for(int j=0;j<n;j++)
            mat[i][j]=0;
    }
    Matrix operator *(const Matrix &b)const{
        Matrix ret=Matrix(n);
        for(int i=0;i<n;i++){
            for(int k=0;k<n;k++){
                if(mat[i][k])
                for(int j=0;j<n;j++){
                    ret.mat[i][j]+=(mat[i][k]*b.mat[k][j]+mod)%mod;
                    ret.mat[i][j]+=mod;
                    ret.mat[i][j]%=mod;
                }
            }
        }
        return ret;
    }
    ull pow_m(ull a,int n){
        ull ret=1,tmp=a;
        while(n){
            if(n&1)ret*=tmp;
            tmp*=tmp;
            n>>=1;
        }
        return ret;
    }
    Matrix pow_M(Matrix a,ll n){
        Matrix ret=Matrix(a.n);
        for(int i=0;i<a.n;i++)ret.mat[i][i]=1;
        Matrix tmp=a;
        while(n){
            if(n&1)ret=ret*tmp;
            tmp=tmp*tmp;
            n>>=1;
        }
        return ret;
    }
};
ll num[20];
ll sum[20];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    ll n,m;
    while(cin>>n>>m){
        Matrix a=Matrix(n+2);
        num[0]=0;
        for(int i=1;i<=n;i++)cin>>num[i];
        sum[0]=233;
        for(int i=1;i<=n;i++)sum[i]=sum[i-1]+num[i];
        sum[n+1]=3;
        if(m==0){
            cout<<num[m]<<endl;continue;
        }
        else if(m==1){
            cout<<sum[m]<<endl;continue;
        }
        else{
            for(int i=0;i<n+1;i++)a.mat[i][0]=10;
            for(int i=1;i<n+1;i++){
                for(int j=1;j<=i;j++){
                    a.mat[i][j]=1;
                }
            }
            for(int i=0;i<n+2;i++)a.mat[i][n+1]=1;
          /*  for(int i=0;i<n+2;i++){
                for(int j=0;j<n+2;j++){
                    cout<<a.mat[i][j]<<" ";
                }
                cout<<endl;
            }*/
            a=a.pow_M(a,m-1);
            ll ans=0;
            ll anw[15]={0};
            for(int i=0;i<n+2;i++){
                for(int j=0;j<n+2;j++){
                    anw[i]=(anw[i]+(a.mat[i][j]*sum[j])%mod)%mod;
                }
            }
            cout<<anw[n]%mod<<endl;
        }
    }
    return 0;
}

C.HDU - 4990 Reading comprehension

题意

题目给我们一个O(N)求值程序让我们求这个值在操作N次后的答案

n&1->ans=ans*2+1;

else->ans=ans*2;

题解

因为数据量很大(1e9)所以很可能会超时，所以只能用加速算法

现在我们考虑只有偶数项

$A[n]=A[n-1]*2;\\A[n-1]=A[n-2]*2+1; \\A[n]=4*A[n-2]+2$

如果是偶数就直接求n/2次方，如果是奇数就求出二次方后再*2+1；

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define pp pair<int,int>
//const ll mod=1e7+7;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
ll mod;
struct Matrix{
    ll mat[15][15];
    int n;
    Matrix(){}
    Matrix(int _n){
        n=_n;
        for(int i=0;i<n;i++)
            for(int j=0;j<n;j++)
            mat[i][j]=0;
    }
    Matrix operator *(const Matrix &b)const{
        Matrix ret=Matrix(n);
        for(int i=0;i<n;i++){
            for(int k=0;k<n;k++){
                if(mat[i][k])
                for(int j=0;j<n;j++){
                    ret.mat[i][j]+=(mat[i][k]*b.mat[k][j]+mod)%mod;
                    ret.mat[i][j]+=mod;
                    ret.mat[i][j]%=mod;
                }
            }
        }
        return ret;
    }
    ull pow_m(ull a,int n){
        ull ret=1,tmp=a;
        while(n){
            if(n&1)ret*=tmp;
            tmp*=tmp;
            n>>=1;
        }
        return ret;
    }
    Matrix pow_M(Matrix a,ll n){
        Matrix ret=Matrix(a.n);
        for(int i=0;i<a.n;i++)ret.mat[i][i]=1;
        Matrix tmp=a;
        while(n){
            if(n&1)ret=ret*tmp;
            tmp=tmp*tmp;
            n>>=1;
        }
        return ret;
    }
};
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    ll n,m;
    while(cin>>n>>m){
        mod=m;
        Matrix a=Matrix(2);
        a.mat[0][0]=4;a.mat[0][1]=1;
        a.mat[1][0]=0;a.mat[1][1]=1;
        if(n&1){
            a=a.pow_M(a,n/2);
            cout<<((((a.mat[0][1]*2)%mod)*2%mod)+1)%mod<<endl;
        }
        else{
            a=a.pow_M(a,n/2);
            cout<<(a.mat[0][1]*2)%mod<<endl;
        }
    }
    return 0;
}

E.HDU - 4965 Fast Matrix Calculation

题意

题意很简单，给你一个N×K的矩阵A，再给你一个K×N的矩阵B N<=1000,K<=6

1.求出矩阵C=A×B

2.求出矩阵C^n*n

3.求出矩阵C的和

题解

一开始直接模拟，于是很愉快的超时了，发现如果是A×B 是N×N的矩阵1000×1000

于是一个骚操作出现了A×B的N的平方的平方可以才成A×B×A×B×A…×B 于是可以变成A×(B×A)^(n×n-1)×B 这里B×A是6×6的矩阵速度快的一批；长见识了！

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=6;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
ll x,y;
typedef vector<ll>vec;
typedef vector<vec>mat;
mat mul(mat& A,mat &B){
    mat C(A.size(),vec(B[0].size()));
    for(int i=0;i<A.size();i++)
        for(int k=0;k<B.size();k++)
        if(A[i][k])
            for(int j=0;j<B[0].size();j++)
            C[i][j]=(C[i][j]+A[i][k]*B[k][j]%mod+mod)%mod;
    return C;
}
mat Pow(mat A,ll n){
    mat B(A.size(),vec(A.size()));
    for(int i=0;i<A.size();i++)B[i][i]=1;
    for(;n;n>>=1,A=mul(A,A))
        if(n&1)B=mul(B,A);
    return B;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    ll n,k;
    while(cin>>n>>k){
        if(n==0&&k==0)break;
        mat a(n,vec(k));
        mat b(k,vec(n));
        for(int i=0;i<n;i++)
        for(int j=0;j<k;j++)
            cin>>a[i][j];
        for(int i=0;i<k;i++)
            for(int j=0;j<n;j++)
            cin>>b[i][j];
        mat c=mul(b,a);
        ll nn=n*n-1;
        c=Pow(c,nn);
        a=mul(a,c);
        a=mul(a,b);
        ll sum=0;
        for(int i=0;i<a.size();i++){
            for(int j=0;j<a[0].size();j++){
                sum+=a[i][j];
            }
        }
        cout<<sum<<endl;
    }
    return 0;
}

G.UVA - 10689 Yet another Number Sequence

水题不解释了

int t;
cin>>t;
while(t--){
    ll n,m,a,b;
    cin>>a>>b>>n>>m;
    mod=1;
    while(m--)mod*=10;
    mat aa=mat(2,vec(2));
    aa[0][0]=1;aa[0][1]=1;aa[1][0]=1;aa[1][1]=0;
    if(n==0){cout<<a%mod<<endl;continue;}
    if(n==1){cout<<b%mod<<endl;continue;}
    aa=Pow(aa,n-1);
    mat bb=mat(2,vec(1));
    bb[0][0]=b%mod;bb[1][0]=a%mod;
    bb=mul(aa,bb);
    cout<<bb[0][0]%mod<<endl;
}

H.UVA - 11149 Power of Matrix

题意

计算矩阵A^1+A^2+A^3+…A^k

题解

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=10;
const int maxn=10;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
ll x,y;
typedef vector<ll>vec;
typedef vector<vec>mat;
mat mul(mat& A,mat &B){
    mat C(A.size(),vec(B[0].size()));
    for(int i=0;i<A.size();i++)
        for(int k=0;k<B.size();k++)
        if(A[i][k])
            for(int j=0;j<B[0].size();j++)
            C[i][j]=(C[i][j]+A[i][k]*B[k][j]%mod+mod)%mod;
    return C;
}
mat Pow(mat A,ll n){
    mat B(A.size(),vec(A.size()));
    for(int i=0;i<A.size();i++)B[i][i]=1;
    for(;n;n>>=1,A=mul(A,A))
        if(n&1)B=mul(B,A);
    return B;
}
mat add(mat& A,mat& B){
    mat C(A.size(),vec(A[0].size()));
    for(int i=0;i<A.size();i++){
        for(int j=0;j<A[0].size();j++){
            C[i][j]=(A[i][j]+B[i][j])%mod;
        }
    }
    return C;
}
mat slove(mat& A,ll n){
    if(n==1)return A;
    mat B=slove(A,n/2);
    mat er=Pow(A,n/2);
    er=mul(B,er);
    mat sum=add(B,er);//B+B*A(1/2)
    er=Pow(A,n);
    if(n&1)sum=add(sum,er);
    return sum;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n;
    ll k;
    while(cin>>n>>k){
        if(n==0)break;
        mat a=mat(n,vec(n));
        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                cin>>a[i][j];
                a[i][j]%=mod;
            }
        }
        a=slove(a,k);
        for(int i=0;i<n;i++){
            for(int j=0;j<n-1;j++){
                cout<<a[i][j]<<" ";
            }
            cout<<a[i][n-1]<<endl;
        }
        cout<<endl;
    }
    return 0;
}

I.UVA - 10655 Contemplation! Algebra

题意

给出a+b的值和ab的值，求a^n+b^n的值

题解

令a+b=A，ab=B，S(n)=a^n+b^n。则S(n)=a^n+b^n=(a+b)(a^n-1+b^n-1)-abn-1-an-1b=(a+b)(a^n-1+b^n-1)-ab(a^n-2+b^n-2)=A×S(n-1)-B×S(n-2)　　（n≥2)。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
ll mod;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
typedef vector<ll>vec;
typedef vector<vec>mat;
mat mul(mat &A,mat &B){
    mat C(A.size(),vec(B[0].size()));
    for(int i=0;i<A.size();i++)
        for(int k=0;k<B.size();k++)
        if(A[i][k])
        for(int j=0;j<B[0].size();j++)
            C[i][j]=C[i][j]+A[i][k]*B[k][j];
    return C;
}
mat Pow(mat A,ll n){
    mat B(A.size(),vec(A.size()));
    for(int i=0;i<A.size();i++)B[i][i]=1;
    for(;n;n>>=1,A=mul(A,A))
        if(n&1)B=mul(B,A);
    return B;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    ll p,q,n;
    while(cin>>p>>q>>n){
        mat a(2,vec(2));
        a[0][0]=p;a[0][1]=-q;
        a[1][0]=1;a[1][1]=0;
        if(n==0)cout<<2<<endl;
        else if(n==1)cout<<p<<endl;
        else{
            a=Pow(a,n-1);
            mat b(2,vec(1));
            b[0][0]=p;b[1][0]=2;
            a=mul(a,b);
            cout<<a[0][0]<<endl;
        }
    }
    return 0;
}

M.HDU - 4565 So Easy!

题意

a,b,n,m都是整数，Sn向上取整并且(a-1)^2<b<a^2

题解

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
ll mod;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
typedef vector<ll>vec;
typedef vector<vec>mat;
mat mul(mat &A,mat &B){
    mat C(A.size(),vec(B[0].size()));
    for(int i=0;i<A.size();i++)
        for(int k=0;k<B.size();k++)
        if(A[i][k])
        for(int j=0;j<B[0].size();j++)
            C[i][j]=(C[i][j]+A[i][k]*B[k][j]%mod+mod)%mod;
    return C;
}
mat Pow(mat A,ll n){
    mat B(A.size(),vec(A.size()));
    for(int i=0;i<A.size();i++)B[i][i]=1;
    for(;n;n>>=1,A=mul(A,A))
        if(n&1)B=mul(B,A);
    return B;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    ll a,b,n,m;
    while(cin>>a>>b>>n>>m){
        mod=m;
        mat AA=mat(2,vec(2));
        AA[0][0]=2*a;AA[0][1]=-(a*a-b);
        AA[1][0]=1;AA[1][1]=0;
        AA=Pow(AA,n);
        cout<<((((AA[1][0]*2)%mod)*a)%mod+(AA[1][1]*2)%mod+mod)%mod<<endl;
    }
    return 0;
}

R.HDU - 4549 M斐波那契数列

题意

中文题

题解

直接做做不来的，列举几个情况

0 a
1 b
2 a*b
3 a*b^2
4 a^2*b^3
5 a^3*b^5
6 a^5*b^8
7 a^8*b^13

很容易看出a和b的项数各自符合斐波那契数列然后可以用矩阵求出各自的项数，再用快速幂求出结果

注意因为这里的项数太大所以要使用费马小定理/欧拉降幂

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=1e9+7;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
ll x,y;
typedef vector<ll>vec;
typedef vector<vec>mat;
mat mul(mat& A,mat &B,ll mod){
    mat C(A.size(),vec(B[0].size()));
    for(int i=0;i<A.size();i++)
        for(int k=0;k<B.size();k++)
        if(A[i][k])
            for(int j=0;j<B[0].size();j++)
            C[i][j]=(C[i][j]+A[i][k]*B[k][j]%mod+mod)%mod;
    return C;
}
mat Pow(mat A,ll n){
    mat B(A.size(),vec(A.size()));
    for(int i=0;i<A.size();i++)B[i][i]=1;
    for(;n;n>>=1,A=mul(A,A,mod-1))
        if(n&1)B=mul(B,A,mod-1);
    return B;
}
ll pow_m(ll a,int n){
    ll ret=1,tmp=a;
    while(n){
        if(n&1)ret=(ret*tmp)%mod;
        tmp=(tmp*tmp)%mod;
        n>>=1;
    }
    return ret;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    ll a,b,n;
    while(cin>>a>>b>>n){
        mat A=mat(2,vec(2));
        A[0][0]=1;A[0][1]=1;A[1][0]=1;A[1][1]=0;
        if(n==0){cout<<a<<endl;continue;}
        if(n==1){cout<<b<<endl;continue;}
        mat B=Pow(A,n-2);
        ll aa=B[0][0]%(mod-1);
        //cout<<"aa="<<aa<<endl;
        aa=pow_m(a,aa);
        //cout<<"aa="<<aa<<endl;
        ll bb=(B[0][0]+B[0][1])%(mod-1);
        //cout<<"bb="<<bb<<endl;
        bb=pow_m(b,bb);
        //cout<<"bb="<<bb<<endl;
        cout<<(aa*bb)%mod<<endl;

    }
    return 0;
}

S.HDU - 4686 Arc of Dream

题意

An Arc of Dream is a curve defined by following function:

where
a0 = A0
ai = ai-1×AX+AY
b0 = B0
bi = bi-1×BX+BY
What is the value of AoD(N) modulo 1,000,000,007?

题意太好理解了就不解释了

题解

kuangbin

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=1e9+7;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
typedef vector<ll>vec;
typedef vector<vec>mat;
mat mul(mat &A,mat &B){
    mat C(A.size(),vec(B[0].size()));
    for(int i=0;i<A.size();i++)
        for(int k=0;k<B.size();k++)
        if(A[i][k])
        for(int j=0;j<B[0].size();j++)
            C[i][j]=(C[i][j]+A[i][k]*B[k][j]%mod+mod)%mod;
    return C;
}
mat Pow(mat A,ll n){
    mat B(A.size(),vec(A.size()));
    for(int i=0;i<A.size();i++)B[i][i]=1;
    for(;n;n>>=1,A=mul(A,A))
        if(n&1)B=mul(B,A);
    return B;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    ll n,a0,AX,AY,b0,BX,BY;
    while(cin>>n){
        cin>>a0>>AX>>AY;
        cin>>b0>>BX>>BY;
        a0%=mod;AX%=mod;AY%=mod;
        b0%=mod;BX%=mod;BY%=mod;
        mat a=mat(5,vec(5));
        a[0][0]=AX*BX%mod;a[0][1]=AX*BY%mod;a[0][2]=AY*BX%mod;a[0][3]=AY*BY%mod;a[0][4]=0;
        a[1][0]=0;a[1][1]=AX%mod;a[1][2]=0;a[1][3]=AY%mod;a[1][4]=0;
        a[2][0]=0;a[2][1]=0;a[2][2]=BX%mod;a[2][3]=BY%mod;a[2][4]=0;
        a[3][0]=0;a[3][1]=0;a[3][2]=0;a[3][3]=1;a[3][4]=0;
        a[4][0]=1;a[4][1]=0;a[4][2]=0;a[4][3]=0;a[4][4]=1;
        a=Pow(a,n);
       /* for(int i=0;i<5;i++){
            for(int j=0;j<5;j++){
                cout<<a[i][j]<<'\t';
            }
            cout<<endl;
        }*/
        mat b=mat(5,vec(1));
        b[0][0]=a0*b0%mod;b[1][0]=a0%mod;b[2][0]=b0%mod;b[3][0]=1;b[4][0]=0;
        b=mul(a,b);
        cout<<b[4][0]<<endl;
        //cout<<((a[4][0]*a0*b0)%mod+(a[4][1]*a0)%mod+(a[4][2]*b0)%mod+(a[4][3])%mod+mod)%mod<<endl;
    }
    return 0;
}

「kuangbin带你飞」专题十八后缀数组

Diposting di 2019-04-24 | Edited on 2018-11-28

传送门

倍增法

struct DA{
    bool cmp(int *r,int a,int b,int l){
        return r[a]==r[b]&&r[a+l]==r[b+l];
    }
    int t1[maxn],t2[maxn],c[maxn];
    int rank[maxn],height[maxn],RMQ[maxn],mm[maxn];
    int best[20][maxn];
    int r[maxn];
    int sa[maxn];
    int str[maxn];
    void da(int n,int m){
        n++;
        int i,j,p,*x=t1,*y=t2;
        for(i=0;i<m;i++)c[i]=0;
        for(i=0;i<n;i++)c[x[i]=str[i]]++;
        for(i=1;i<m;i++)c[i]+=c[i-1];
        for(i=n-1;i>=0;i--)sa[--c[x[i]]]=i;
        for(j=1;j<=n;j<<=1){
            p=0;
            for(i=n-j;i<n;i++)y[p++]=i;
            for(i=0;i<n;i++)if(sa[i]>=j)y[p++]=sa[i]-j;
            for(i=0;i<m;i++)c[i]=0;
            for(i=0;i<n;i++)c[x[y[i]]]++;
            for(i=1;i<m;i++)c[i]+=c[i-1];
            for(i=n-1;i>=0;i--)sa[--c[x[y[i]]]]=y[i];
            swap(x,y);
            p=1;x[sa[0]]=0;
            for(i=1;i<n;i++)
                x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++;
            if(p>=n)break;
            m=p;
        }
        int k=0;
        n--;
        for(i=0;i<=n;i++)rank[sa[i]]=i;
        for(i=0;i<n;i++){
            if(k)k--;
            j=sa[rank[i]-1];
            while(str[i+k]==str[j+k])k++;
            height[rank[i]]=k;
        }
    }
    void initRMQ(int n){
        for(int i=1;i<=n;i++)RMQ[i]=height[i];
        mm[0]=-1;
        for(int i=1;i<=n;i++)
            mm[i]=((i&(i-1))==0)?mm[i-1]+1:mm[i-1];
        for(int i=1;i<=n;i++)best[0][i]=i;
        for(int i=1;i<=mm[n];i++)
        for(int j=1;j+(1<<i)-1<=n;j++){
            int a=best[i-1][j];
            int b=best[i-1][j+(1<<(i-1))];
            if(RMQ[a]<RMQ[b])best[i][j]=a;
            else best[i][j]=b;
        }
    }
    int askRMQ(int a,int b){
        int t;
        t=mm[b-a+1];
        b-=(1<<t)-1;
        a=best[t][a];b=best[t][b];
        return RMQ[a]<RMQ[b]?a:b;
    }
    int lcp(int a,int b){
        a=rank[a];b=rank[b];
        if(a>b)swap(a,b);
        return height[askRMQ(a+1,b)];
    }
    void print(int n){
        cout<<"sa[] ";
        for(int i=0;i<=n;i++)cout<<sa[i]<<" ";cout<<endl;
        cout<<"rank[] ";
        for(int i=0;i<=n;i++)cout<<rank[i]<<" ";cout<<endl;
        cout<<"height[] ";
        for(int i=0;i<=n;i++)cout<<height[i]<<" ";cout<<endl;
    }
}AA,BB;

A.POJ1743 Musical Theme

题意

有N(1<=N<=20000)个音符的序列来表示一首乐曲，每个音符都是1..88范围内的整数，现在要找一个重复的子串，它需要满足如下条件：1.长度至少为5个音符。
2.在乐曲中重复出现（就是出现过至少两次）。(可能经过转调，“转调”的意思是主题序列中每个音符都被加上或减去了同一个整数值)
3.重复出现的同一主题不能有公共部分。

思路

对于第一二点:至少长度是五,我们可以二分0-n/2之间的长度来查找height(height[i]=排名为i和i-1的后缀子串的最长公共前缀长度缀)然后找到两个大于二分的值,然后判断起点距离是否大于二分的值(因为要求不重叠)</br>
第三点因为共同加上一个值,但是他们前后的差值还是一样的(例如1，2，3和5，6，7是一样的他们的差值是1)然后把原数组变成一个长度为N-1的数组去处理,因为处理后的数组比原数组少1所以答案也要-1;

//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=2e5;
const ll inf=0x3f3f3f3f3f3f;
#define bug cout<<"here:"<<endl;
int sa[maxn];
//sa[i]名次为i的后缀的起始位置;
//Rank[i]起始位置为i的名次 ->Rank[sa[i]]=i;
//height[i]名次为i和i-1的后缀的最长公共前缀长;
int t1[maxn],t2[maxn],c[maxn];
int Rank[maxn],height[maxn];
bool cmp(int *r,int a,int b,int l){
    return r[a]==r[b]&&r[a+l]==r[b+l];
}
int s[maxn];
void da(int str[],int n,int m){
    int i,j,p,*x=t1,*y=t2;
    for(i=0;i<m;i++)c[i]=0;
    for(i=0;i<n;i++)c[x[i]=str[i]]++;//***
    for(i=1;i<m;i++)c[i]+=c[i-1];
    for(i=n-1;i>=0;i--)sa[--c[x[i]]]=i;
    for(j=1;j<=n;j<<=1){
        p=0;
        for(i=n-j;i<n;i++)y[p++]=i;
        for(i=0;i<n;i++)if(sa[i]>=j)y[p++]=sa[i]-j;
        for(i=0;i<m;i++)c[i]=0;
        for(i=0;i<n;i++)c[x[y[i]]]++;
        for(i=1;i<m;i++)c[i]+=c[i-1];
        for(i=n-1;i>=0;i--)sa[--c[x[y[i]]]]=y[i];
        swap(x,y);
        p=1;x[sa[0]]=0;
        for(i=1;i<n;i++)
            x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++;
        if(p>=n)break;
        m=p;
    }
    int k=0;
    n--;
    for(i=0;i<=n;i++)Rank[sa[i]]=i;
    for(i=0;i<n;i++){
        if(k)k--;
        j=sa[Rank[i]-1];
        while(s[i+k]==s[j+k])k++;
        height[Rank[i]]=k;
    }
}

bool isok(int n,int k){
    int ma=sa[1],mi=sa[1];
    for(int i=2;i<=n;i++){
        if(height[i]<k)ma=mi=sa[i];
        else{
            if(sa[i]<mi)mi=sa[i];
            if(sa[i]>ma)ma=sa[i];
            if(ma-mi>k)return true;
        }
    }return false;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n;
    while(cin>>n&&n){
        for(int i=0;i<n;i++)cin>>s[i];
        for(int i=n-1;i>0;i--)s[i]=s[i]-s[i-1]+90;//因为四十行要用s[i]的值做下表所以不能出现负数
        n--;//变化后的长度-1
        for(int i=0;i<n;i++)s[i]=s[i+1];
        s[n]=0;
        da(s,n+1,200);

        int ans=-1;
        int l=1,r=n/2;
        while(l<=r){
            int mid=(l+r)/2;
            if(isok(n,mid)){
                ans=mid;
                l=mid+1;
            }
            else r=mid-1;
        }
        if(ans<4)cout<<0<<endl;
        else cout<<ans+1<<endl;
    }
    return 0;
}

附加1. #1403 : 后缀数组一·重复旋律

题意

最长可重叠重复K次子串问题。

题解

二分答案

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
#define rank rankk
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
int t1[maxn],t2[maxn],c[maxn];
bool cmp(int *r,int a,int b,int l){
    return r[a]==r[b]&&r[a+l]==r[b+l];
}
void da(int str[],int sa[],int rank[],int height[],int n,int m){
    n++;
    int i,j,p,*x=t1,*y=t2;
    for(i=0;i<m;i++)c[i]=0;
    for(i=0;i<n;i++)c[x[i]=str[i]]++;
    for(i=1;i<m;i++)c[i]+=c[i-1];
    for(i=n-1;i>=0;i--)sa[--c[x[i]]]=i;
    for(j=1;j<=n;j<<=1){
        p=0;
        for(i=n-j;i<n;i++)y[p++]=i;
        for(i=0;i<n;i++)if(sa[i]>=j)y[p++]=sa[i]-j;
        for(i=0;i<m;i++)c[i]=0;
        for(i=0;i<n;i++)c[x[y[i]]]++;
        for(i=1;i<m;i++)c[i]+=c[i-1];
        for(i=n-1;i>=0;i--)sa[--c[x[y[i]]]]=y[i];
        swap(x,y);
        p=1;x[sa[0]]=0;
        for(i=1;i<n;i++)
            x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++;
        if(p>=n)break;
        m=p;
    }
    int k=0;
    n--;
    for(i=0;i<=n;i++)rank[sa[i]]=i;
    for(i=0;i<n;i++){
        if(k)k--;
        j=sa[rank[i]-1];
        while(str[i+k]==str[j+k])k++;
        height[rank[i]]=k;
    }
}
int rank[maxn];//后缀i在sa[]中的排名
int height[maxn];//sa[i]与sa[i-1]的LCP(最长公共前缀)
int str[maxn];
int r[maxn];
int sa[maxn];//sa[i]表示排名弟i小的后缀的下标
int n,m;
int solve(int k){
    int tmp=1;
    for(int i=1;i<n;){
        int cnt=1;
        int j=i+1;
        while(height[j]>=k&&j<=n)j++,cnt++;
        tmp=max(cnt,tmp);
        i=j;
    }
    return tmp>=m;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    cin>>n>>m;
    for(int i=0;i<n;i++)cin>>str[i];
    str[n]=0;//多补一个0
    da(str,sa,rank,height,n,128);
    int l=0,r=n,ans=-1;
    while(l<=r){
        int mid=(l+r)>>1;
        if(solve(mid))ans=mid,l=mid+1;
        else r=mid-1;
    }
    cout<<ans<<endl;
    return 0;
}

附加2. #1407 : 后缀数组二·重复旋律2

题意

最长不可重叠重复子串问题

题解

只要判断长度是否大于二分的就行

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
#define rank rankk
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
int t1[maxn],t2[maxn],c[maxn];
bool cmp(int *r,int a,int b,int l){
    return r[a]==r[b]&&r[a+l]==r[b+l];
}
void da(int str[],int sa[],int rank[],int height[],int n,int m){
    n++;
    int i,j,p,*x=t1,*y=t2;
    for(i=0;i<m;i++)c[i]=0;
    for(i=0;i<n;i++)c[x[i]=str[i]]++;
    for(i=1;i<m;i++)c[i]+=c[i-1];
    for(i=n-1;i>=0;i--)sa[--c[x[i]]]=i;
    for(j=1;j<=n;j<<=1){
        p=0;
        for(i=n-j;i<n;i++)y[p++]=i;
        for(i=0;i<n;i++)if(sa[i]>=j)y[p++]=sa[i]-j;
        for(i=0;i<m;i++)c[i]=0;
        for(i=0;i<n;i++)c[x[y[i]]]++;
        for(i=1;i<m;i++)c[i]+=c[i-1];
        for(i=n-1;i>=0;i--)sa[--c[x[y[i]]]]=y[i];
        swap(x,y);
        p=1;x[sa[0]]=0;
        for(i=1;i<n;i++)
            x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++;
        if(p>=n)break;
        m=p;
    }
    int k=0;
    n--;
    for(i=0;i<=n;i++)rank[sa[i]]=i;
    for(i=0;i<n;i++){
        if(k)k--;
        j=sa[rank[i]-1];
        while(str[i+k]==str[j+k])k++;
        height[rank[i]]=k;
    }
}
int rank[maxn];//后缀i在sa[]中的排名
int height[maxn];//sa[i]与sa[i-1]的LCP(最长公共前缀)
int str[maxn];
int r[maxn];
int sa[maxn];//sa[i]表示排名弟i小的后缀的下标
int n,m;
int solve(int k){
    int minsa,maxsa;
    for(int i=1;i<=n;i++)
    if(height[i]<k){
        minsa=sa[i];
        maxsa=sa[i];
    }
    else{
        minsa=min(minsa,sa[i]);
        maxsa=max(maxsa,sa[i]);
        if(maxsa-minsa>=k)return true;
    }
    return false;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    cin>>n;
    for(int i=0;i<n;i++)cin>>str[i];
    str[n]=0;//多补一个0
    da(str,sa,rank,height,n,1280);
    int l=0,r=n,ans=-1;
    while(l<=r){
        int mid=(l+r)>>1;
        if(solve(mid))ans=mid,l=mid+1;
        else r=mid-1;
    }
    cout<<ans<<endl;
    return 0;
}

附加3.#1415 : 后缀数组三·重复旋律3

题意

经典的最长公共子串问题//

如果同一段旋律在作品A和作品B中同时出现过，这段旋律就是A和B共同的部分，比如在abab 在 bababab 和 cabacababc 中都出现过。小Hi想知道两部作品的共同旋律最长是多少？

题解

把两个字符串接在一起就变成了求后缀的最长公共前缀的问题，但是由于这个前缀不能跨越两个字符串，所以我们在第一个字符串后面加上一个没有出现过的字符，再接第二个字符串，然后取所有非同一个串后缀的height的最大值…

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
#define rank rankk
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
int t1[maxn],t2[maxn],c[maxn];
bool cmp(int *r,int a,int b,int l){
    return r[a]==r[b]&&r[a+l]==r[b+l];
}
void da(char str[],int sa[],int rank[],int height[],int n,int m){
    n++;
    int i,j,p,*x=t1,*y=t2;
    for(i=0;i<m;i++)c[i]=0;
    for(i=0;i<n;i++)c[x[i]=str[i]]++;
    for(i=1;i<m;i++)c[i]+=c[i-1];
    for(i=n-1;i>=0;i--)sa[--c[x[i]]]=i;
    for(j=1;j<=n;j<<=1){
        p=0;
        for(i=n-j;i<n;i++)y[p++]=i;
        for(i=0;i<n;i++)if(sa[i]>=j)y[p++]=sa[i]-j;
        for(i=0;i<m;i++)c[i]=0;
        for(i=0;i<n;i++)c[x[y[i]]]++;
        for(i=1;i<m;i++)c[i]+=c[i-1];
        for(i=n-1;i>=0;i--)sa[--c[x[y[i]]]]=y[i];
        swap(x,y);
        p=1;x[sa[0]]=0;
        for(i=1;i<n;i++)
            x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++;
        if(p>=n)break;
        m=p;
    }
    int k=0;
    n--;
    for(i=0;i<=n;i++)rank[sa[i]]=i;
    for(i=0;i<n;i++){
        if(k)k--;
        j=sa[rank[i]-1];
        while(str[i+k]==str[j+k])k++;
        height[rank[i]]=k;
    }
}
int rank[maxn];//后缀i在sa[]中的排名
int height[maxn];//sa[i]与sa[i-1]的LCP(最长公共前缀)
char str[maxn];
char str2[maxn];
int r[maxn];
int sa[maxn];//sa[i]表示排名弟i小的后缀的下标
int n,m;
int solve(int n,int len1){
    int ans=0;
    for(int i=1;i<=n;i++){
        if((sa[i-1]<=len1&&sa[i]>len1)||(sa[i-1]>len1&&sa[i]<=len1))
            ans=max(ans,height[i]);
    }
    return ans;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    cin>>str;
    int len1=strlen(str);
    str[len1]='#';
    cin>>str2;
    int len2=strlen(str2);
    for(int i=0;i<len2;i++){
        str[len1+1+i]=str2[i];
    }
    str[len1+1+len2]=0;
    n=len1+len2+1;
    da(str,sa,rank,height,n,128);
    cout<<solve(n,len1)<<endl;
    return 0;
}

附加4.#1419 : 后缀数组四·重复旋律4

题意

重复次数最多的连续字串

小Hi平时的一大兴趣爱好就是演奏钢琴。我们知道一个音乐旋律被表示为长度为 N 的数构成的数列。小Hi在练习过很多曲子以后发现很多作品中的旋律有重复的部分。

我们把一段旋律称为(k,l)-重复的，如果它满足由一个长度为l的字符串重复了k次组成。如旋律abaabaabaaba是(4,3)重复的，因为它由aba重复4次组成。

小Hi想知道一部作品中k最大的(k,l)-重复旋律。

题解

求重复次数最多的连续字串

假如知道了这个连续子串的开始位置
并且知道了它的长度
那么，此时我们就通过lcp(i,i+len)来进行比较即可

但是，如果枚举长度和开始的位置的话
尽管lcp通过st表可以O(1)查询
但是这个枚举的复杂度是O(n2)的
很显然，需要更快

所以，枚举了长度lenlen之后
我们只需要考虑开始位置为lenlen倍数的地方
如果此时有一个重复串的开始位置不在lenlen的倍数上
很显然的
lcp就会多出一截
所以，我们可以倒推出这个位置
所以，这样枚举复杂度为O(nlogn)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
#define rank rankk
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
int t1[maxn],t2[maxn],c[maxn];
bool cmp(int *r,int a,int b,int l){
    return r[a]==r[b]&&r[a+l]==r[b+l];
}
void da(char str[],int sa[],int rank[],int height[],int n,int m){
    n++;
    int i,j,p,*x=t1,*y=t2;
    for(i=0;i<m;i++)c[i]=0;
    for(i=0;i<n;i++)c[x[i]=str[i]]++;
    for(i=1;i<m;i++)c[i]+=c[i-1];
    for(i=n-1;i>=0;i--)sa[--c[x[i]]]=i;
    for(j=1;j<=n;j<<=1){
        p=0;
        for(i=n-j;i<n;i++)y[p++]=i;
        for(i=0;i<n;i++)if(sa[i]>=j)y[p++]=sa[i]-j;
        for(i=0;i<m;i++)c[i]=0;
        for(i=0;i<n;i++)c[x[y[i]]]++;
        for(i=1;i<m;i++)c[i]+=c[i-1];
        for(i=n-1;i>=0;i--)sa[--c[x[y[i]]]]=y[i];
        swap(x,y);
        p=1;x[sa[0]]=0;
        for(i=1;i<n;i++)
            x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++;
        if(p>=n)break;
        m=p;
    }
    int k=0;
    n--;
    for(i=0;i<=n;i++)rank[sa[i]]=i;
    for(i=0;i<n;i++){
        if(k)k--;
        j=sa[rank[i]-1];
        while(str[i+k]==str[j+k])k++;
        height[rank[i]]=k;
    }
}
int rank[maxn];//后缀i在sa[]中的排名
int height[maxn];//sa[i]与sa[i-1]的LCP(最长公共前缀)
int RMQ[maxn];
int mm[maxn];
int best[20][maxn];
void initRMQ(int n){
    mm[0]=-1;
    for(int i=1;i<=n;i++)
        mm[i]=((i&(i-1))==0)?mm[i-1]+1:mm[i-1];
    for(int i=1;i<=n;i++)best[0][i]=i;
    for(int i=1;i<=mm[n];i++)
    for(int j=1;j+(1<<i)-1<=n;j++){
        int a=best[i-1][j];
        int b=best[i-1][j+(1<<(i-1))];
        if(RMQ[a]<RMQ[b])best[i][j]=a;
        else best[i][j]=b;
    }
}
int askRMQ(int a,int b){
    int t;
    t=mm[b-a+1];
    b-=(1<<t)-1;
    a=best[t][a];b=best[t][b];
    return RMQ[a]<RMQ[b]?a:b;
}
int lcp(int a,int b){//求以a,b开始的字串的最长公共前缀
    a=rank[a];b=rank[b];
    if(a>b)swap(a,b);
    return height[askRMQ(a+1,b)];
}
char str[maxn];
int r[maxn];
int sa[maxn];//sa[i]表示排名弟i小的后缀的下标
int n,m;
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    cin>>str;
    n=strlen(str);
    str[n]=0;
    da(str,sa,rank,height,n,128);
    for(int i=1;i<=n;i++)RMQ[i]=height[i];
    initRMQ(n);
    int ans=1;
    for(int i=1;i<=n;i++){
        for(int j=0;j+i<n;j+=i){
            int len=lcp(j,j+i);
            int k=j-(i-len%i);
            int sum=len/i+1;
            if(k>=0&&lcp(k,k+i)>=i){
                sum++;
            }
            ans=max(ans,sum);
        }
    }
    cout<<ans<<endl;
    return 0;
}

B.UVA - 10829 Gap Substrings

题意

题目即求有多少子串满足ABA的形式，并且满足|A|>0，|B|=G。

题解

搞了我三天三夜的题目

首先可以用后缀数组求出任意两个点的后缀的lcp,然后相同长度减去g就是答案

但是这样复杂度是n^2

然后我们可以发现假设A的长度是L，第一个L在K位置,那么另一个L是K+L+G

然后我们发现如果L和另一个K+L+G判断相同了之后，那么L+1,L+2，…2L-1其实都不用再匹配了

所以我们就直接枚举长度L 然后在0，L，2L，3L进行匹配，注意不仅仅要向后面匹配前缀，还要向前面匹配后缀，后者我们可以把字符串倒置，然后求n-1-k，和n-1-(k+l+g)的lcp 这样两个lcp相加，那A的起点就可以在他们这个范围里面所以答案就是lcp1+lcp2-L

注意lcp长度不能超过L,因为超过的话就会访问到另一个L的区域了

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
struct DA{
    bool cmp(int *r,int a,int b,int l){
        return r[a]==r[b]&&r[a+l]==r[b+l];
    }
    int t1[maxn],t2[maxn],c[maxn];
    int rank[maxn],height[maxn],RMQ[maxn],mm[maxn];
    int best[20][maxn];
    int r[maxn];
    int sa[maxn];
    int str[maxn];
    void da(int n,int m){
        n++;
        int i,j,p,*x=t1,*y=t2;
        for(i=0;i<m;i++)c[i]=0;
        for(i=0;i<n;i++)c[x[i]=str[i]]++;
        for(i=1;i<m;i++)c[i]+=c[i-1];
        for(i=n-1;i>=0;i--)sa[--c[x[i]]]=i;
        for(j=1;j<=n;j<<=1){
            p=0;
            for(i=n-j;i<n;i++)y[p++]=i;
            for(i=0;i<n;i++)if(sa[i]>=j)y[p++]=sa[i]-j;
            for(i=0;i<m;i++)c[i]=0;
            for(i=0;i<n;i++)c[x[y[i]]]++;
            for(i=1;i<m;i++)c[i]+=c[i-1];
            for(i=n-1;i>=0;i--)sa[--c[x[y[i]]]]=y[i];
            swap(x,y);
            p=1;x[sa[0]]=0;
            for(i=1;i<n;i++)
                x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++;
            if(p>=n)break;
            m=p;
        }
        int k=0;
        n--;
        for(i=0;i<=n;i++)rank[sa[i]]=i;
        for(i=0;i<n;i++){
            if(k)k--;
            j=sa[rank[i]-1];
            while(str[i+k]==str[j+k])k++;
            height[rank[i]]=k;
        }
    }
    void initRMQ(int n){
        for(int i=1;i<=n;i++)RMQ[i]=height[i];
        mm[0]=-1;
        for(int i=1;i<=n;i++)
            mm[i]=((i&(i-1))==0)?mm[i-1]+1:mm[i-1];
        for(int i=1;i<=n;i++)best[0][i]=i;
        for(int i=1;i<=mm[n];i++)
        for(int j=1;j+(1<<i)-1<=n;j++){
            int a=best[i-1][j];
            int b=best[i-1][j+(1<<(i-1))];
            if(RMQ[a]<RMQ[b])best[i][j]=a;
            else best[i][j]=b;
        }
    }
    int askRMQ(int a,int b){
        int t;
        t=mm[b-a+1];
        b-=(1<<t)-1;
        a=best[t][a];b=best[t][b];
        return RMQ[a]<RMQ[b]?a:b;
    }
    int lcp(int a,int b){
        a=rank[a];b=rank[b];
        if(a>b)swap(a,b);
        return height[askRMQ(a+1,b)];
    }
    void print(int n){
        cout<<"sa[] ";
        for(int i=0;i<=n;i++)cout<<sa[i]<<" ";cout<<endl;
        cout<<"rank[] ";
        for(int i=0;i<=n;i++)cout<<rank[i]<<" ";cout<<endl;
        cout<<"height[] ";
        for(int i=0;i<=n;i++)cout<<height[i]<<" ";cout<<endl;
    }
}AA,BB;
char s[maxn];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    /*int len=strlen(s);
    for(int i=0;i<len;i++)AA.str[i]=s[i];
    AA.da(len,120);
    AA.print(len);*/
    int t;
    cin>>t;
    int CC=1;
    while(t--){
        int g;
        cin>>g>>s;
        int len=strlen(s);
        //cout<<"s=="<<s<<endl;
        //cout<<"len="<<len<<endl;
        for(int i=0;i<len;i++){
            AA.str[i]=s[i]-'a'+1;
            BB.str[i]=s[len-i-1]-'a'+1;
        }
        AA.da(len,30);BB.da(len,30);
        AA.initRMQ(len);BB.initRMQ(len);
        //AA.print(len);
       // BB.print(len);
        ll ans=0;
        for(int i=1;i<=len;i++){
            for(int j=0;j+i+g<len;j+=i){
                int l=j,r=j+i+g;
                int lll=min(i,AA.lcp(l,r));
                int rrr=min(i,BB.lcp(len-l-1,len-r-1));
                int len=(lll+rrr);
                if(len>=i)ans+=ll(1LL*len-i);
            }
        }
        cout<<"Case "<<CC++<<": ";
        cout<<ans<<endl;
    }
    return 0;
}
/*
2
1 bbaabaaaaa
5 abxxxxxab
*/

dc3

struct DA{
    #define F(x) ((x)/3+((x)%3==1?0:tb))
    #define G(x) ((x)<tb?(x)*3+1:((x)-tb)*3+2)
    int sa[maxn*20],rank[maxn*20],height[maxn*20],str[maxn*20];
    int wa[maxn*20],wb[maxn*20],wv[maxn*20],wss[maxn*20];
    int c0(int *r,int a,int b){
        return r[a]==r[b]&&r[a+1]==r[b+1]&&r[a+2]==r[b+2];
    }
    int c12(int k,int *r,int a,int b){
        if(k==2)
            return r[a]<r[b]||(r[a]==r[b]&&c12(1,r,a+1,b+1));
        else return r[a]<r[b]||(r[a]==r[b]&&wv[a+1]<wv[b+1]);
    }
    void sort(int *r,int *a,int *b,int n,int m){
        int i;
        for(i=0;i<n;i++)wv[i]=r[a[i]];
        for(i=0;i<m;i++)wss[i]=0;
        for(i=0;i<n;i++)wss[wv[i]]++;
        for(i=1;i<m;i++)wss[i]+=wss[i-1];
        for(i=n-1;i>=0;i--)
            b[--wss[wv[i]]]=a[i];
    }
    void dc3(int *r,int *sa,int n,int m){
        int i,j,*rn=r+n;
        int *san=sa+n,ta=0,tb=(n+1)/3,tbc=0,p;
        r[n]=r[n+1]=0;
        for(i=0;i<n;i++)if(i%3!=0)wa[tbc++]=i;
        sort(r+2,wa,wb,tbc,m);
        sort(r+1,wb,wa,tbc,m);
        sort(r,wa,wb,tbc,m);
        for(p=1,rn[F(wb[0])]=0,i=1;i<tbc;i++)
            rn[F(wb[i])]=c0(r,wb[i-1],wb[i])?p-1:p++;
        if(p<tbc)dc3(rn,san,tbc,p);
        else for(i=0;i<tbc;i++)san[rn[i]]=i;
        for(i=0;i<tbc;i++)if(san[i]<tb)wb[ta++]=san[i]*3;
        if(n%3==1)wb[ta++]=n-1;
        sort(r,wb,wa,ta,m);
        for(i=0;i<tbc;i++)wv[wb[i]=G(san[i])]=i;
        for(i=0,j=0,p=0;i<ta&&j<tbc;p++)
            sa[p]=c12(wb[j]%3,r,wa[i],wb[j])?wa[i++]:wb[j++];
        for(;i<ta;p++)sa[p]=wa[i++];
        for(;j<tbc;p++)sa[p]=wb[j++];
    }
    void da(int n,int m){
        for(int i=n;i<n*3;i++)str[i]=0;
        dc3(str,sa,n+1,m);
        int i,j,k=0;
        for(i=0;i<=n;i++)rank[sa[i]]=i;
        for(i=0;i<n;i++){
            if(k)k--;
            j=sa[rank[i]-1];
            while(str[i+k]==str[j+k])k++;
            height[rank[i]]=k;
        }
    }
    void print(int n){
        cout<<"sa[] ";
        for(int i=0;i<=n;i++)cout<<sa[i]<<" ";cout<<endl;
        cout<<"rank[] ";
        for(int i=0;i<=n;i++)cout<<rank[i]<<" ";cout<<endl;
        cout<<"height[] ";
        for(int i=0;i<=n;i++)cout<<height[i]<<" ";cout<<endl;
    }
}DA;

A.Mediocre String Problem （2018南京M,回文+LCP)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
struct DA{
    #define F(x) ((x)/3+((x)%3==1?0:tb))
    #define G(x) ((x)<tb?(x)*3+1:((x)-tb)*3+2)
    int sa[maxn*20],rank[maxn*20],height[maxn*20],str[maxn*20];
    int wa[maxn*20],wb[maxn*20],wv[maxn*20],wss[maxn*20];
    int c0(int *r,int a,int b){
        return r[a]==r[b]&&r[a+1]==r[b+1]&&r[a+2]==r[b+2];
    }
    int c12(int k,int *r,int a,int b){
        if(k==2)
            return r[a]<r[b]||(r[a]==r[b]&&c12(1,r,a+1,b+1));
        else return r[a]<r[b]||(r[a]==r[b]&&wv[a+1]<wv[b+1]);
    }
    void sort(int *r,int *a,int *b,int n,int m){
        int i;
        for(i=0;i<n;i++)wv[i]=r[a[i]];
        for(i=0;i<m;i++)wss[i]=0;
        for(i=0;i<n;i++)wss[wv[i]]++;
        for(i=1;i<m;i++)wss[i]+=wss[i-1];
        for(i=n-1;i>=0;i--)
            b[--wss[wv[i]]]=a[i];
    }
    void dc3(int *r,int *sa,int n,int m){
        int i,j,*rn=r+n;
        int *san=sa+n,ta=0,tb=(n+1)/3,tbc=0,p;
        r[n]=r[n+1]=0;
        for(i=0;i<n;i++)if(i%3!=0)wa[tbc++]=i;
        sort(r+2,wa,wb,tbc,m);
        sort(r+1,wb,wa,tbc,m);
        sort(r,wa,wb,tbc,m);
        for(p=1,rn[F(wb[0])]=0,i=1;i<tbc;i++)
            rn[F(wb[i])]=c0(r,wb[i-1],wb[i])?p-1:p++;
        if(p<tbc)dc3(rn,san,tbc,p);
        else for(i=0;i<tbc;i++)san[rn[i]]=i;
        for(i=0;i<tbc;i++)if(san[i]<tb)wb[ta++]=san[i]*3;
        if(n%3==1)wb[ta++]=n-1;
        sort(r,wb,wa,ta,m);
        for(i=0;i<tbc;i++)wv[wb[i]=G(san[i])]=i;
        for(i=0,j=0,p=0;i<ta&&j<tbc;p++)
            sa[p]=c12(wb[j]%3,r,wa[i],wb[j])?wa[i++]:wb[j++];
        for(;i<ta;p++)sa[p]=wa[i++];
        for(;j<tbc;p++)sa[p]=wb[j++];
    }
    void da(int n,int m){
        for(int i=n;i<n*3;i++)str[i]=0;
        dc3(str,sa,n+1,m);
        int i,j,k=0;
        for(i=0;i<=n;i++)rank[sa[i]]=i;
        for(i=0;i<n;i++){
            if(k)k--;
            j=sa[rank[i]-1];
            while(str[i+k]==str[j+k])k++;
            height[rank[i]]=k;
        }
    }
    void print(int n){
        cout<<"sa[] ";
        for(int i=0;i<=n;i++)cout<<sa[i]<<" ";cout<<endl;
        cout<<"rank[] ";
        for(int i=0;i<=n;i++)cout<<rank[i]<<" ";cout<<endl;
        cout<<"height[] ";
        for(int i=0;i<=n;i++)cout<<height[i]<<" ";cout<<endl;
    }
}DA;
struct PalTree{
    int next[maxn][26],fail[maxn],cnt[maxn],num[maxn],len[maxn],S[maxn],last,n,p;
    int newnode(int l){
        for(int i=0;i<26;i++)next[p][i]=0;
        cnt[p]=num[p]=0;len[p]=l;return p++;
    }
    void init(){
        p=0;newnode(0);newnode(-1);last=0;n=0;S[n]=-1;fail[0]=1;
    }
    int get_fail(int x){
        while(S[n-len[x]-1]!=S[n])x=fail[x];return x;
    }
    int add(int c){
        c-='a';S[++n]=c;int cur=get_fail(last);
        if(!next[cur][c]){
            int now=newnode(len[cur]+2);
            fail[now]=next[get_fail(fail[cur])][c];
            next[cur][c]=now;num[now]=num[fail[now]]+1;
        }
        last=next[cur][c];cnt[last]++;return num[last];
    }
    void count(){for(int i=p-1;i>=0;i--)cnt[fail[i]]+=cnt[i];}
}PAM;
char s[maxn],t[maxn];
int num[maxn],cnt[maxn];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    cin>>s>>t;
    int lens=strlen(s),lent=strlen(t);
    int len=0;PAM.init();
    for(int i=0;i<lens;i++)DA.str[len++]=s[lens-i-1]-'a'+1,cnt[lens-i-1]=PAM.add(s[lens-i-1]);
    DA.str[len++]=30;
    for(int i=0;i<lent;i++)DA.str[len++]=t[i]-'a'+1;
    DA.str[len]=0;
    DA.da(len,200);
	int p=DA.rank[lens+1];
	//DA.print(len);
	int now=len+1;
	for(int i=p-1;i>=0;i--){
		now=min(now,DA.height[i+1]);
		if(DA.sa[i]>=0&&DA.sa[i]<lens){
			num[lens-1-DA.sa[i]]=now;
		}
	}
	now=len+1;
	for(int i=p+1;i<=len;i++){
		now=min(now,DA.height[i]);
		if(DA.sa[i]>=0&&DA.sa[i]<lens){
			num[lens-1-DA.sa[i]]=now;
		}
	}
	ll ans=0;
    for(int i=0;i<lens-1;i++){
        ans+=1LL*num[i]*cnt[i+1];
    }
    cout<<ans<<endl;
    return 0;
}

I.POJ - 3415 Common Substrings

单调栈优化

题意

求长度不小于K的公共子串的个数。

题解

对于一个LCP 贡献是len(lcp)-k+1

我们可以将height进行分组，大于等于k的在同一组，如果两个后缀的最长公共子串>=k，那么它们肯定在同一个组内。现在从头开始扫，每遇到A的后缀时，就统计一下它和它前面的B的后缀能组成多少长度>=k的公共子串，然后再反过来处理B的后缀即可，一共需要扫两遍。但是这样的时间复杂度是O(n^2)，是行不通的。

因为两个后缀的LCP是它们之间的最小height值，所以可以维护一个自底向上递增的单调栈，如果有height值小于了当前栈顶的height值，那么大于它的那些只能按照当前这个小的值来计算。这样分别处理两次，一次处理A的后缀，一次处理B的后缀。需要记录好栈里的和以及每个组内的后缀数。

注意longlong

18.I1

#include<string>
#include<iostream>
#include<iosfwd>
#include<cmath>
#include<cstring>
#include<stdlib.h>
#include<stdio.h>
#include<cstring>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=998244353;
const int maxn=2e5+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
struct DA{
    #define F(x) ((x)/3+((x)%3==1?0:tb))
    #define G(x) ((x)<tb?(x)*3+1:((x)-tb)*3+2)
    int sa[maxn*10],rank[maxn*10],height[maxn*10],str[maxn*10];
    int wa[maxn*10],wb[maxn*10],wv[maxn*10],wss[maxn*10];
    int RMQ[maxn],mm[maxn],best[20][maxn];;
    int c0(int *r,int a,int b){
        return r[a]==r[b]&&r[a+1]==r[b+1]&&r[a+2]==r[b+2];
    }
    int c12(int k,int *r,int a,int b){
        if(k==2)
            return r[a]<r[b]||(r[a]==r[b]&&c12(1,r,a+1,b+1));
        else return r[a]<r[b]||(r[a]==r[b]&&wv[a+1]<wv[b+1]);
    }
    void sort(int *r,int *a,int *b,int n,int m){
        int i;
        for(i=0;i<n;i++)wv[i]=r[a[i]];
        for(i=0;i<m;i++)wss[i]=0;
        for(i=0;i<n;i++)wss[wv[i]]++;
        for(i=1;i<m;i++)wss[i]+=wss[i-1];
        for(i=n-1;i>=0;i--)
            b[--wss[wv[i]]]=a[i];
    }
    void dc3(int *r,int *sa,int n,int m){
        int i,j,*rn=r+n;
        int *san=sa+n,ta=0,tb=(n+1)/3,tbc=0,p;
        r[n]=r[n+1]=0;
        for(i=0;i<n;i++)if(i%3!=0)wa[tbc++]=i;
        sort(r+2,wa,wb,tbc,m);
        sort(r+1,wb,wa,tbc,m);
        sort(r,wa,wb,tbc,m);
        for(p=1,rn[F(wb[0])]=0,i=1;i<tbc;i++)
            rn[F(wb[i])]=c0(r,wb[i-1],wb[i])?p-1:p++;
        if(p<tbc)dc3(rn,san,tbc,p);
        else for(i=0;i<tbc;i++)san[rn[i]]=i;
        for(i=0;i<tbc;i++)if(san[i]<tb)wb[ta++]=san[i]*3;
        if(n%3==1)wb[ta++]=n-1;
        sort(r,wb,wa,ta,m);
        for(i=0;i<tbc;i++)wv[wb[i]=G(san[i])]=i;
        for(i=0,j=0,p=0;i<ta&&j<tbc;p++)
            sa[p]=c12(wb[j]%3,r,wa[i],wb[j])?wa[i++]:wb[j++];
        for(;i<ta;p++)sa[p]=wa[i++];
        for(;j<tbc;p++)sa[p]=wb[j++];
    }
    void da(int n,int m){
        for(int i=n;i<n*3;i++)str[i]=0;
        dc3(str,sa,n+1,m);
        int i,j,k=0;
        for(i=0;i<=n;i++)rank[sa[i]]=i;
        for(i=0;i<n;i++){
            if(k)k--;
            j=sa[rank[i]-1];
            while(str[i+k]==str[j+k])k++;
            height[rank[i]]=k;
        }
    }

    void initRMQ(int n){
        for(int i=1;i<=n;i++)RMQ[i]=height[i];
        mm[0]=-1;
        for(int i=1;i<=n;i++)
            mm[i]=((i&(i-1))==0)?mm[i-1]+1:mm[i-1];
        for(int i=1;i<=n;i++)best[0][i]=i;
        for(int i=1;i<=mm[n];i++)
        for(int j=1;j+(1<<i)-1<=n;j++){
            int a=best[i-1][j];
            int b=best[i-1][j+(1<<(i-1))];
            if(RMQ[a]<RMQ[b])best[i][j]=a;
            else best[i][j]=b;
        }
    }
    int askRMQ(int a,int b){
        int t;
        t=mm[b-a+1];
        b-=(1<<t)-1;
        a=best[t][a];b=best[t][b];
        return RMQ[a]<RMQ[b]?a:b;
    }
    int lcp(int a,int b){
        a=rank[a];b=rank[b];
        if(a>b)swap(a,b);
        return height[askRMQ(a+1,b)];
    }
    void print(int n){
        cout<<"sa[] ";
        for(int i=0;i<=n;i++)cout<<sa[i]<<" ";cout<<endl;
        cout<<"rank[] ";
        for(int i=0;i<=n;i++)cout<<rank[i]<<" ";cout<<endl;
        cout<<"height[] ";
        for(int i=0;i<=n;i++)cout<<height[i]<<" ";cout<<endl;
    }
}DA;
char str[maxn],str1[maxn];
int s[maxn][2];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int k;
    while(cin>>k&&k){
        cin>>str>>str1;
        int lena=strlen(str);
        int lenb=strlen(str1);
        int n=0;
        for(int i=0;i<lena;i++)DA.str[n++]=str[i];
        DA.str[n++]=1;
        for(int i=0;i<lenb;i++)DA.str[n++]=str1[i];
        DA.da(n,300);
        ll tot=0,top=0;
        ll sum=0;
        for(int i=1;i<=n;i++){
            if(DA.height[i]<k)top=0,tot=0;
            else{
                ll cnt=0;
                if(DA.sa[i-1]<lena){
                    cnt++;tot+=(ll)DA.height[i]-k+1;
                }
                while(top&&DA.height[i]<=s[top-1][0]){
                    top--;
                    tot+=(ll)s[top][1]*(DA.height[i]-s[top][0]);
                    cnt+=(ll)s[top][1];
                }
                s[top][0]=DA.height[i];s[top++][1]=cnt;
                if(DA.sa[i]>lena)sum+=tot;
            }
        }
        tot=top=0;
        for(int i=1;i<=n;i++){
            if(DA.height[i]<k)top=0,tot=0;
            else{
                int cnt=0;
                if(DA.sa[i-1]>lena){
                    cnt++;tot+=(ll)DA.height[i]-k+1;
                }
                while(top&&DA.height[i]<=s[top-1][0]){
                    top--;
                    tot+=(ll)s[top][1]*(DA.height[i]-s[top][0]);
                    cnt+=(ll)s[top][1];
                }
                s[top][0]=DA.height[i];s[top++][1]=cnt;
                if(DA.sa[i]<lena)sum+=tot;
            }
        }
        cout<<sum<<endl;
    }
    return 0;
}

luowentaoaa

嘤嘤嘤

125 posting

53 tags

P2257 YY的GCD

P3327 [SDOI2015]约数个数和

[ZJOI2008]树的统计 （入门题,链最大值,链和）

思路

P2486 [SDOI2011]染色 (区间操作很难 未AC)

P3258 [JLOI2014]松鼠的新家 (区间加减)

P3834 【模板】可持久化线段树 1（主席树）

P2617 Dynamic Rankings (主席树套树状数组)

P3157 [CQOI2011]动态逆序对 (主席树套树状数组)

思路

思路

思路

P1306 斐波那契公约数 (gcd(Fn,Fm)=F(gcd(n,m)))

思路

P1967 货车运输 （最大生成树+LCA）

P1613 跑路 （倍增+floyd）

DFS

八皇后

思路

单词方阵

思路

迷宫

比较水的题

BFS

填图颜色

思路

01迷宫(联通块加速)

思路

马的遍历（水）

带有技巧的搜索

总结

模板

A.BZOJ-2460 [BeiJing2011]元素

B.LightOJ - 1422 Halloween Costumes

题意

题解

C.POJ - 2955 Brackets

题意

题解

D.CodeForces - 149D Coloring Brackets

题意

题解

E.POJ - 1651 Multiplication Puzzle

题意

题解1

题解2

G.HDU - 4283 You Are the One

题意

题意

H.HDU - 2476 String painter

题意

题解

A.HDU - 3507 Print Article

题意

题解

A.CodeForces - 450B Jzzhu and Sequences

题意

题解

B.HDU - 5015 233 Matrix

题意

题解

C.HDU - 4990 Reading comprehension

题意

题解

E.HDU - 4965 Fast Matrix Calculation

题意

题解

G.UVA - 10689 Yet another Number Sequence

H.UVA - 11149 Power of Matrix

题意

题解

I.UVA - 10655 Contemplation! Algebra

题意

题解

M.HDU - 4565 So Easy!

题意

题解

R.HDU - 4549 M斐波那契数列

题意

题解

[ZJOI2008]树的统计（入门题,链最大值,链和）

P2486 [SDOI2011]染色 (区间操作很难未AC)

P1967 货车运输（最大生成树+LCA）

P1613 跑路（倍增+floyd）