树形DP

Diposting di 2019-04-24 | Edited on 2018-11-21

传送门

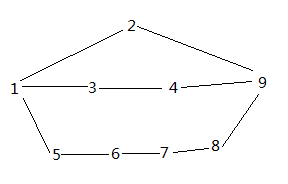
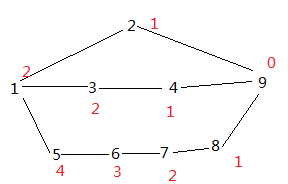
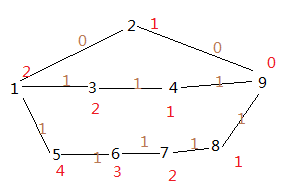
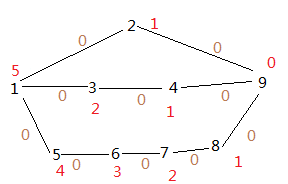
A.HDU - 1520 Anniversary party

父亲结点和子结点不能同取

题意

给出一棵树每个节点有权值要求父节点和子节点不能同时取求能够取得的最大值

思路

dp[now]0 表示不取当前结点

dp[now]1 表示取当前结点

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
int happy[maxn],dp[maxn][2],father[maxn],n;
vector<int>ve[maxn];
void dfs(int x){
    dp[x][0]=0;
    dp[x][1]=happy[x];
    for(int i=0;i<ve[x].size();i++){
        int v=ve[x][i];
        dfs(v);
        dp[x][0]+=max(dp[v][0],dp[v][1]);
        dp[x][1]+=dp[v][0];
    }
    return ;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    while(cin>>n){
    for(int i=1;i<=n;i++){
        cin>>happy[i];
        ve[i].clear();
        dp[i][0]=dp[i][1]=0;
        father[i]=-1;
    }
    while(true){
        int a,b;
        cin>>a>>b;
        if(!a&&!b)break;
        ve[b].push_back(a);
        father[a]=b;
    }
    for(int i=1;i<=n;i++){
        if(father[i]==-1){
            dfs(i);
            cout<<max(dp[i][0],dp[i][1])<<endl;
            break;
        }
    }
    }
    return 0;
}

B.POJ - 1655 Balancing Act

树的重心

题意

求某个点：以这个点为根结点的子树中顶点个数的最大值作为这个点的价值，那么找出价值最小的点，并且输出最小值，价值相等输出靠前的点。

题解

就是求树的重心。

树的重心：树的重心也叫树的质心。找到一个点,其所有的子树中最大的子树节点数最少,那么这个点就是这棵树的重心,删去重心后，生成的多棵树尽可能平衡。

dp|now|[1]表示以p为根的子树节点个数（包括本身），dp[p]0]表示以p为balance node的最大子集个数。

#include<iostream>
#include<algorithm>
#include<vector>
#include<cstring>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=998244353;
const int maxn=2e4+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
/*struct node{
    int to;
    int dep;
};*/
vector<int>ve[maxn];
int dp[maxn][2];
void init(int n){
    memset(dp,0,sizeof(dp));
    for(int i=0;i<=n;i++)ve[i].clear();
}
void dfs(int now,int pre,int n){
    dp[now][0]=0;dp[now][1]=1;
    for(int i=0;i<ve[now].size();i++){
        int to=ve[now][i];
        if(to==pre)continue;
        dfs(to,now,n);
        dp[now][1]+=dp[to][1];
        dp[now][0]=max(dp[now][0],dp[to][1]);
    }
    dp[now][0]=max(dp[now][0],n-dp[now][1]);
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int t;
    cin>>t;
    while(t--){
        int n;
        cin>>n;
        init(n);
        for(int i=1;i<n;i++){
            int a,b;
            cin>>a>>b;
            ve[a].push_back(b);
            ve[b].push_back(a);
        }
        dfs(1,-1,n);
        int mi=inf,mid;
        for(int i=1;i<=n;i++){
            if(mi>dp[i][0])mi=dp[i][0],mid=i;
        }
        cout<<mid<<" "<<mi<<endl;
    }
    return 0;
}

C.HDU - 2196 Computer

给出一棵树，求离每个节点最远的点的距离

题解

可以知道最远距离肯定要么是当前结点到自己的叶子结点，或者当前结点到另一个其他结点的叶子结点

自己的叶子结点可以dfs递归求出

其他结点的递归结点可以通过自己父亲的最远结点距离得到，但是如果自己就是父亲的最远距离那就只能用次远距离了，所以要同时存储最远子结点和次远子结点

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=998244353;
const int maxn=1e4+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
int n;
struct node{
    int to,cap;
};
vector<node>ve[maxn];
int dp[maxn][3];
void init(int n){
    for(int i=0;i<=n;i++)ve[i].clear();
    memset(dp,0,sizeof(dp));
}
void dfs(int now,int pre){
    int mx=0,mx2=0;
    for(int i=0;i<ve[now].size();i++){
        int nex=ve[now][i].to;
        if(nex==pre)continue;
        int ncap=ve[now][i].cap;
        dfs(nex,now);
        if(mx<dp[nex][0]+ncap)mx2=mx,mx=dp[nex][0]+ncap;
        else if(mx2<dp[nex][0]+ncap)mx2=dp[nex][0]+ncap;
    }
    dp[now][0]=mx;
    dp[now][1]=mx2;
}
void dfs1(int now,int pre){
    for(int i=0;i<ve[now].size();i++){
        int nex=ve[now][i].to;
        if(nex==pre)continue;
        int ncap=ve[now][i].cap;
        int mx=0;
        if(ncap+dp[nex][0]==dp[now][0])mx=dp[now][1];
        else mx=dp[now][0];
        dp[nex][2]=max(dp[now][2],mx)+ncap;
        dfs1(nex,now);
    }
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    while(cin>>n){
        init(n);
        for(int i=2;i<=n;i++){
            int a,b;
            cin>>a>>b;
            ve[a].push_back(node{i,b});
            ve[i].push_back(node{a,b});
        }
        dfs(1,-1);
        dfs1(1,-1);
        for(int i=1;i<=n;i++){
            cout<<max(dp[i][0],dp[i][2])<<endl;
        }
    }
    return 0;
}

D.UVA - 12186 Another Crisis

为了让信息传到i，需要的最少人数

题意

一个公司有1个老板和n个员工，n个员工中有普通员工和中级员工
现在进行一次投票，若中级员工管理的普通员工中有T%的人投票，则中级员工也投票并递交给上级员工
求最少需要多少个普通员工投票，投票才能到达老板处

题解

存子结点最少的人数，然后排序再加起来

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=998244353;
const int maxn=1e5+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
vector<int>ve[maxn];
void add(int a,int b){
    ve[a].push_back(b);
}
int k;
int dfs(int now){
    if(ve[now].size()==0)return 1;
    vector<int>ppp;
    for(int i=0;i<ve[now].size();i++)ppp.push_back(dfs(ve[now][i]));
    int ans=0;
    sort(ppp.begin(),ppp.end());
    int kk=ve[now].size()*k;
    if(kk%100)kk/=100,kk++;
    else kk/=100;
    for(int i=0;i<kk;i++)ans+=ppp[i];
    return ans;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n;
    while(cin>>n>>k){
        if(!n&&!k)break;
        for(int i=0;i<=n;i++)ve[i].clear();
        int a;
        for(int i=1;i<=n;i++)cin>>a,add(a,i);
        cout<<dfs(0)<<endl;
    }
    return 0;
}

E.UVA - 1220 Party at Hali-Bula

父亲结点和子结点不同时取并且情况唯一

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
map<string,int>mp;
int cnt;
int getid(string s){
    if(mp.count(s))return mp[s];
    else mp[s]=cnt++;
    return mp[s];
}
vector<int>ve[250];
int dp[250][2];
bool only[250][2];
void dfs(int now){
    if(ve[now].size()==0){
        dp[now][1]=1;dp[now][0]=0;
        return;
    }
    for(int i=0;i<ve[now].size();i++){
        int nex=ve[now][i];
        dfs(nex);
        dp[now][0]+=max(dp[nex][0],dp[nex][1]);
        if(dp[nex][0]==dp[nex][1])only[now][0]=true;
        else if(dp[nex][0]>dp[nex][1])only[now][0]|=only[nex][0];
        else if(dp[nex][0]<dp[nex][1])only[now][0]|=only[nex][1];
        dp[now][1]+=dp[nex][0];
        only[now][1]|=only[nex][0];
    }
    dp[now][1]++;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n;
    string s,t;
    while(cin>>n&&n){
        cnt=0;
        cin>>s;
        mp.clear();
        memset(dp,0,sizeof(dp));
        memset(only,false,sizeof(only));
        for(int i=0;i<=n;i++)ve[i].clear();
        getid(s);
        for(int i=1;i<n;i++){
            cin>>s>>t;
            ve[getid(t)].push_back(getid(s));
        }
        dfs(0);
        if(dp[0][0]==dp[0][1])cout<<dp[0][0]<<" No"<<endl;
        else if(dp[0][0]>dp[0][1])cout<<dp[0][0]<<((only[0][0])?" No":" Yes")<<endl;
        else cout<<dp[0][1]<<((only[0][1])?" No":" Yes")<<endl;
    }
    return 0;
}

G.CodeForces - 461B Appleman and Tree

每个联通块中只有一个黑色的点

题意

给出一棵树，每个点是白色或者黑色，问有多少种方案能够通过去掉一些边使每个联通块中只有一个黑色的点。

题解

每个联通块只有有黑点和没有黑点两个选择设dp{i}[0/1]为以i为根没有或者有黑点

初始化，如果有黑点设 dp{i}[1]=1,dp{i}[0]=0,否则反过来

设v是i的一个子树，

1.如果i要是黑的

1.1 v是黑的：那么只能把V的这条边切掉；方案数是i当前为黑的方案数×v当前为黑的方案数

        连接起来     方案数 i当前为白的方案数×v当前为黑的方案数

1.2 v是白的：那就只能i本身是黑才能连接方案数是i当前为黑的方案数×v当前为白的方案数

2.如果i要是白的

2.1 v是黑的：那么只能选择切掉这条v 方案数是i当前为白的方案数×V当前为黑的方案数

2.2 V是白的：那就只能选择连接这条V，方案数是i当前白的方案数×v当前为白的方案数

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=1e9+7;
const int maxn=1e5+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
vector<int>ve[maxn];
ll dp[maxn][2];
int val[maxn];
void add(int a,int b){
    ve[a].push_back(b);
    ve[b].push_back(a);
}
void dfs(int now,int pre){
    if(val[now]==0)dp[now][0]=1,dp[now][1]=0;
    else dp[now][0]=0,dp[now][1]=1;
    for(auto i:ve[now]){
        if(i==pre)continue;
        dfs(i,now);
        ll a=dp[now][0],b=dp[now][1];
        dp[now][0]=(a*dp[i][0]%mod+a*dp[i][1]%mod)%mod;
        dp[now][1]=(a*dp[i][1]%mod+b*dp[i][0]%mod+dp[i][1]*b%mod)%mod;
    }
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n;
    cin>>n;
    for(int i=1;i<n;i++){
        int x;
        cin>>x;
        add(i,x);
    }
    for(int i=0;i<n;i++)cin>>val[i];
    dfs(0,-1);
    cout<<dp[0][1]<<endl;
    return 0;
}

I.CodeForces - 161D Distance in Tree

长度为K的二元组个数

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=998244353;
const int maxn=5e4+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
vector<int>ve[maxn];
int dp[maxn][550];
void add(int a,int b){
    ve[a].push_back(b);ve[b].push_back(a);
}
ll ans;
int k;
void dfs(int now,int pre){
    dp[now][0]=1;
    for(int i=0;i<ve[now].size();i++){
        int to=ve[now][i];
        if(to==pre)continue;
        dfs(to,now);
        for(int i=0;i<=k;i++)ans+=dp[now][i]*dp[to][k-1-i];
        for(int i=1;i<=k;i++)dp[now][i]+=dp[to][i-1];
    }
   /* for(int i=0;i<=k;i++){
        cout<<"now="<<now<<"\t"<<i<<"\tdp["<<now<<"]"<<"["<<i<<"]"<<endl;
    }*/
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n;
    cin>>n>>k;
    for(int i=1;i<n;i++){
        int a,b;
        cin>>a>>b;
        add(a,b);
    }
    ans=0;
    dfs(1,-1);
    cout<<ans<<endl;
    return 0;
}

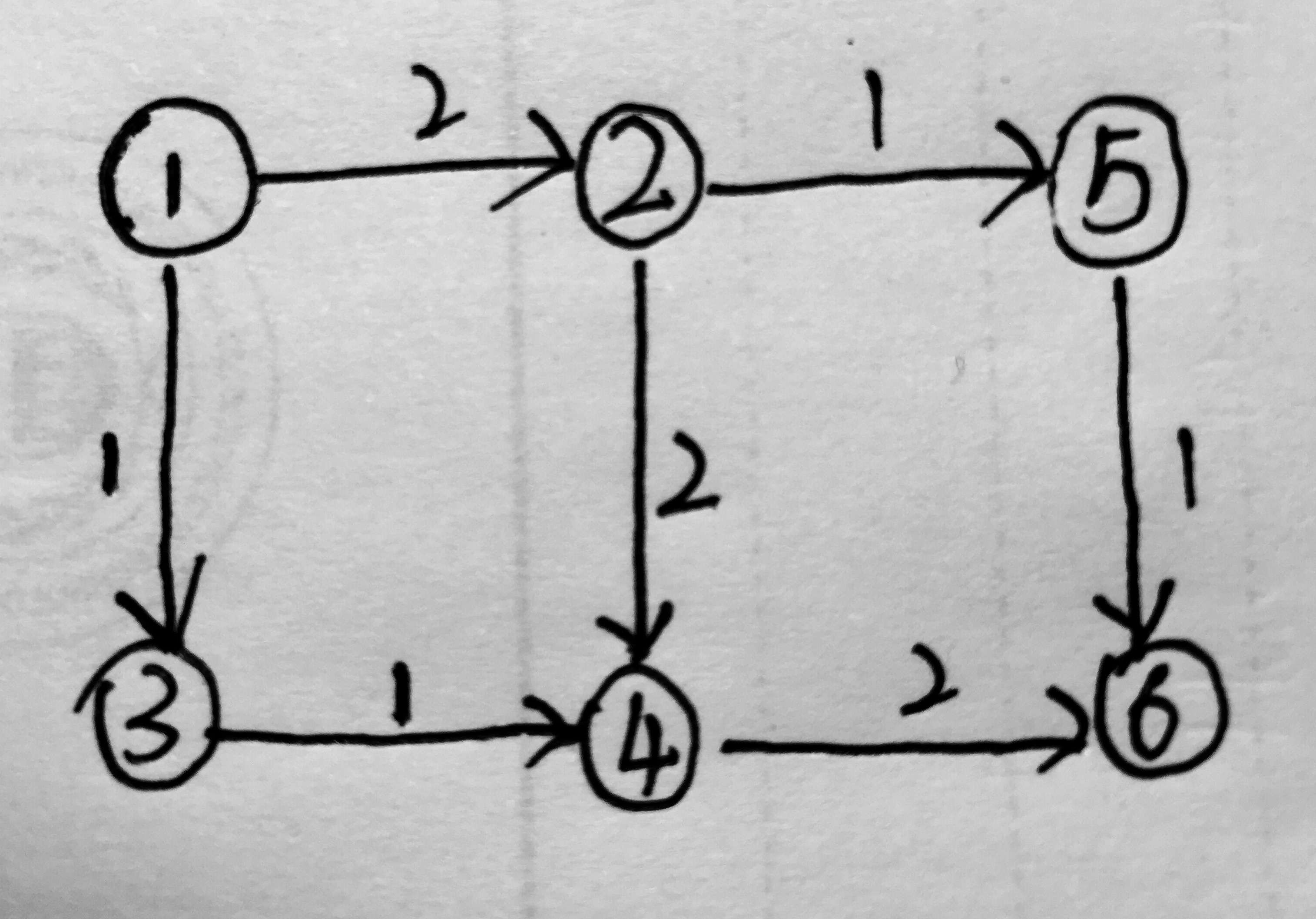
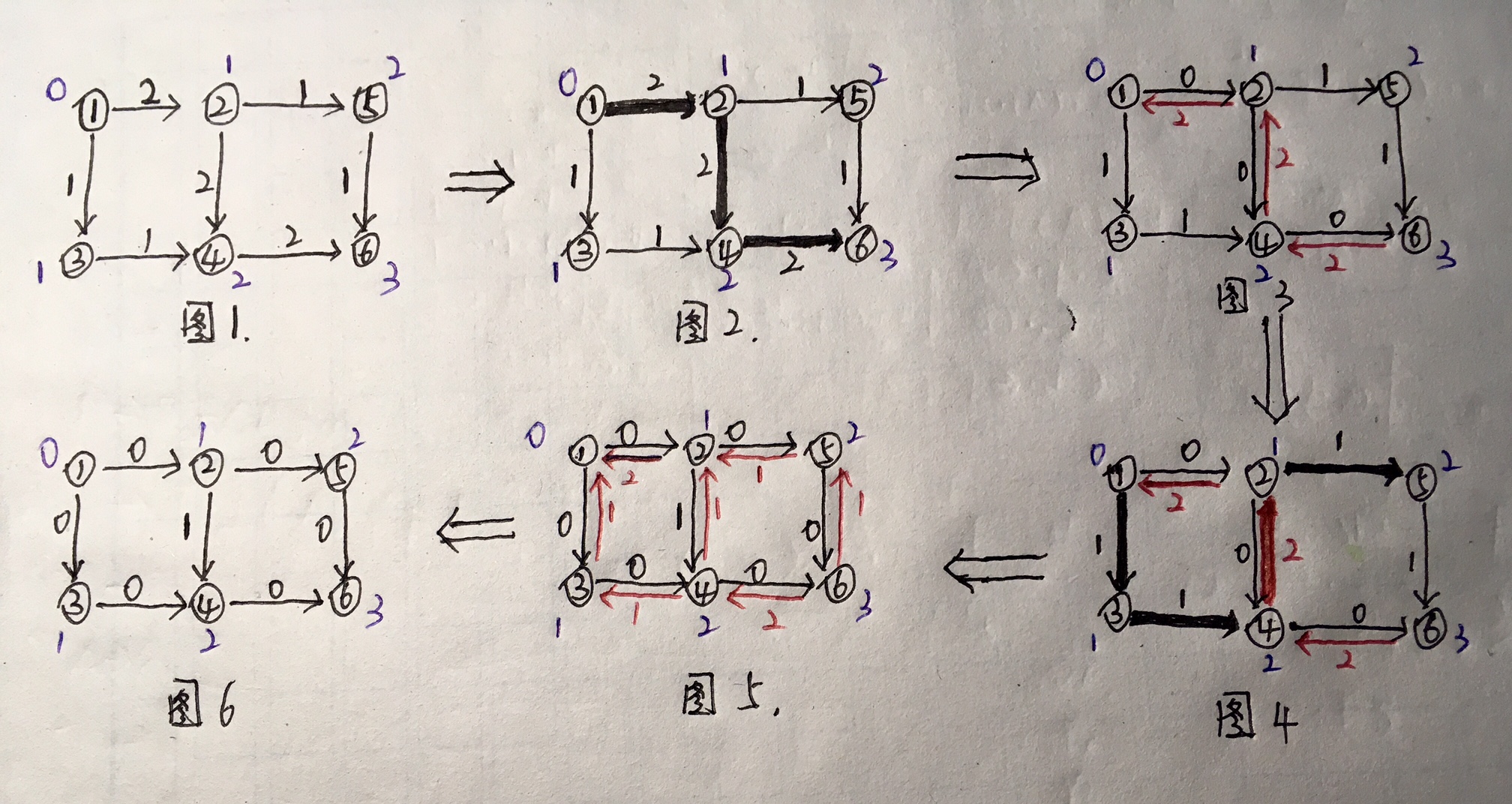
J.CodeForces - 767C Garland

把一个树切成三个权值相同的树

题解

一眼题，但是要注意不仅仅会切成三棵树，有可能切成多个树，所以cnt不能只是==3

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
/*struct node{
    int to;
    int dep;
};*/
vector<int>ve[maxn];
int dp[maxn];
int cnt=0;
int ok[5];
void dfs(int now,int vv){
    for(int i=0;i<ve[now].size();i++){
        int to=ve[now][i];
        dfs(to,vv);
        dp[now]+=dp[to];
    }
    if(dp[now]==vv){
        dp[now]=0;ok[cnt++]=now;
    }
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n;
    cin>>n;
    int root;
    int sum=0;
    for(int i=1;i<=n;i++){
        int a,b;
        cin>>a>>dp[i];
        sum+=dp[i];
        if(!a)root=i;
        else ve[a].push_back(i);
    }
    if(sum%3){cout<<-1<<endl;}
    else{
        dfs(root,sum/3);
        if(cnt>=3)cout<<ok[0]<<" "<<ok[1]<<endl;
        else cout<<-1<<endl;
    }
    return 0;
}

ACM中的正则表达式

Diposting di 2019-04-24 | Edited on 2018-11-17

总结

正则表达式 , 又称规则表达式 , 英文名为 Regular Expression , 在代码中常简写为 regex , regexp 或 RE , 是计算机科学的一个概念 ; 正则表通常被用来检索 , 替换那些符合某个模式 (规则) 的文本 ;

正则表达式是对字符串 (包括普通字符 , 例如 : a 到 z 之间的字母) 和特殊字符 (称为 “元字符” ) 操作的一种逻辑公式 , 就是用事先定义好的一些特定字符 , 及这些特定字符的组合 , 组成一个 “规则字符串” , 这个 “规则字符串” 用来表达对字符串的一种过滤逻辑 ; 正则表达式是一种文本模式 , 模式描述在搜索文本时要匹配的一个或多个字符串 ;

C++对正则表达式的支持

1 2	#include <regex> using namespace std;

运用规则

其实运用规则和Java非常相似!!! 几乎可以完全类推! 
附上一些规则: 
{n}匹配确定的n次 
{n,}至少匹配n次(注:请不要擅自加空格上去) 
{n,m}最少n次,最多m次. 
*匹配前面的子表达式0次或多次 = {0,} 
+匹配前面的子表达式1次或多次 = {1,} 
?匹配前面的子表达式1次或两次 = {1,2} 
()表示一个整体 
[]表示一位 
{}表示匹配多少次 
.匹配除换行符之外的任意字符 
\w匹配单字字符(a-z,A-Z,0-9以及下划线) 
\W匹配非单字字符 
\s匹配空白字符(空格,制表符,换行符) 
\S匹配非空白字符 
\d匹配数字字符 
\D匹配非数字字符 
^指示从行的开始位置开始匹配(还有声明不在字符集指定范围内) 
$指示从行的结束位置开始匹配 
\b匹配单词的开始或结束位置

2.速记理解

. [ ] ^ $四个字符是所有语言都支持的正则表达式，所以这四个是基础的正则表达式。正则难理解因为里面有一个等价的概念，这个概念大大增加了理解难度，让很多初学者看起来会懵，如果把等价都恢复成原始写法，自己书写正则就超级简单了，就像说话一样去写你的正则了：

　　等价：

等价是等同于的意思，表示同样的功能，用不同符号来书写。

?,*,+,\d,\w 都是等价字符
　　?等价于匹配长度{0,1}
　　*等价于匹配长度{0,} 
　　+等价于匹配长度{1,}
　　\d等价于[0-9]

\D等价于[^0-9]
　　\w等价于[A-Za-z_0-9]

\W等价于[^A-Za-z_0-9]。

常用运算符与表达式：
　　^ 开始
　　（） 域段
　　[] 包含,默认是一个字符长度
　　[^] 不包含,默认是一个字符长度
　　{n,m} 匹配长度 
　　. 任何单个字符(\. 字符点)
　　| 或
　　\ 转义
　　$ 结尾
　　[A-Z] 26个大写字母
　　[a-z] 26个小写字母
　　[0-9] 0至9数字

[A-Za-z0-9] 26个大写字母、26个小写字母和0至9数字
　　， 分割
　　分割语法：
　　[A,H,T,W] 包含A或H或T或W字母
　　[a,h,t,w] 包含a或h或t或w字母
　　[0,3,6,8] 包含0或3或6或8数字


　　语法与释义：
　　基础语法 "^([]{})([]{})([]{})$"
　　正则字符串 = "开始（[包含内容]{长度}）（[包含内容]{长度}）（[包含内容]{长度}）结束" 
　　
　　?,*,+,\d,\w 这些都是简写的,完全可以用[]和{}代替，在(?:)(?=)(?!)(?<=)(?<!)(?i)(*?)(+?)这种特殊组合情况下除外。
　　初学者可以忽略?,*,+,\d,\w一些简写标示符，学会了基础使用再按表自己去等价替换
　　
　　实例：
　　字符串；tel:086-0666-88810009999
　　原始正则："^tel:[0-9]{1,3}-[0][0-9]{2,3}-[0-9]{8,11}$" 
　　速记理解：开始 "tel:普通文本"[0-9数字]{1至3位}"-普通文本"[0数字][0-9数字]{2至3位}"-普通文本"[0-9数字]{8至11位} 结束"
　　等价简写后正则写法："^tel:\d{1,3}-[0]\d{2,3}-\d{8,11}$" ，简写语法不是所有语言都支持。

代码中运用实例如下

// 定义一个正则表达式 , 4~23 位数字和字母的组合
regex repPattern("[0-9a-zA-Z]{4,23}",regex_constants::extended);
// 声明匹配结果变量
match_results<string::const_iterator> rerResult;
// 定义待匹配的字符串
string strValue = "123abc";
// 进行匹配
bool bValid = regex_match(strValue, rerResult, repPattern);
if (bValid)
{
    // 匹配成功
}

常用的正则表达式

检验数字的表达式

数字 : ^[0-9]*$
n 位的数字 : ^\d{n}$
至少 n 位的数字 : ^\d{n,}$
m-n 位的数字 : ^\d{m,n}$
零和非零开头的数字 : ^(0|[1-9][0-9]*)$
非零开头的最多带两位小数的数字 : ^([1-9][0-9]*)+(.[0-9]{1,2})?$
带 1~2 位小数的正数或负数 : ^(\-)?\d+(\.\d{1,2})?$
正数 , 负数 , 和小数 : ^(\-|\+)?\d+(\.\d+)?$
有两位小数的正实数 : ^[0-9]+(.[0-9]{2})?$
有 1~3 位小数的正实数 : ^[0-9]+(.[0-9]{1,3})?$
非零的正整数 : ^[1-9]\d*$ 或 ^([1-9][0-9]*){1,3}$ 或 ^\+?[1-9][0-9]*$
非零的负整数 : ^\-[1-9][]0-9″*$ 或 ^-[1-9]\d*$
非负整数 : ^\d+$ 或 ^[1-9]\d*|0$
非正整数 : ^-[1-9]\d*|0$ 或 ^((-\d+)|(0+))$
非负浮点数 : ^\d+(\.\d+)?$ 或 ^[1-9]\d*\.\d*|0\.\d*[1-9]\d*|0?\.0+|0$
非正浮点数 : ^((-\d+(\.\d+)?)|(0+(\.0+)?))$ 或 ^(-([1-9]\d*\.\d*|0\.\d*[1-9]\d*))|0?\.0+|0$
正浮点数 : ^[1-9]\d*\.\d*|0\.\d*[1-9]\d*$ 或 ^(([0-9]+\.[0-9]*[1-9][0-9]*)|([0-9]*[1-9][0-9]*\.[0-9]+)|([0-9]*[1-9][0-9]*))$
负浮点数 : ^-([1-9]\d*\.\d*|0\.\d*[1-9]\d*)$ 或 ^(-(([0-9]+\.[0-9]*[1-9][0-9]*)|([0-9]*[1-9][0-9]*\.[0-9]+)|([0-9]*[1-9][0-9]*)))$
浮点数 : ^(-?\d+)(\.\d+)?$ 或 ^-?([1-9]\d*\.\d*|0\.\d*[1-9]\d*|0?\.0+|0)$

检验字符的表达式

汉字 : ^[\u4e00-\u9fa5]{0,}$
英文和数字 : ^[A-Za-z0-9]+$ 或 ^[A-Za-z0-9]{4,40}$
长度为 3~20 的所有字符 : ^.{3,20}$
由 26 个英文字母组成的字符串 : ^[A-Za-z]+$
由 26 个大写英文字母组成的字符串 : ^[A-Z]+$
由 26 个小写英文字母组成的字符串 : ^[a-z]+$
由数字和 26 个英文字母组成的字符串 : ^[A-Za-z0-9]+$
由数字 , 26 个英文字母或者下划线组成的字符串 : ^\w+$ 或 ^\w{3,20}$
中文 , 英文 , 数字包括下划线 : ^[\u4E00-\u9FA5A-Za-z0-9_]+$
中文 , 英文 , 数字但不包括下划线等符号 : ^[\u4E00-\u9FA5A-Za-z0-9]+$ 或 ^[\u4E00-\u9FA5A-Za-z0-9]{2,20}$
可以输入含有^%&',;=?$\"等字符 : [^%&',;=?$\x22]+
禁止输入含有 ~ 的字符 : [^~\x22]+

特殊需求表达式

Email 地址 : ^\w+([-+.]\w+)*@\w+([-.]\w+)*\.\w+([-.]\w+)*$
域名 : [a-zA-Z0-9][-a-zA-Z0-9]{0,62}(/.[a-zA-Z0-9][-a-zA-Z0-9]{0,62})+/.?
InternetURL : [a-zA-z]+://[^\s]* 或 ^http://([\w-]+\.)+[\w-]+(/[\w-./?%&=]*)?$
手机号码 : ^(13[0-9]|14[5|7]|15[0|1|2|3|5|6|7|8|9]|18[0|1|2|3|5|6|7|8|9])\d{8}$
电话号码("XXX-XXXXXXX" , "XXXX-XXXXXXXX" , "XXX-XXXXXXX" , "XXX-XXXXXXXX" , "XXXXXXX"和"XXXXXXXX) : ^($$\d{3,4}-)|\d{3.4}-)?\d{7,8}$
国内电话号码 (0511-4405222 , 021-87888822) : \d{3}-\d{8}|\d{4}-\d{7}
身份证号 (15 位 , 18 位数字) : ^\d{15}|\d{18}$
短身份证号码 (数字 , 字母 x 结尾) : ^([0-9]){7,18}(x|X)?$ 或 ^\d{8,18}|[0-9x]{8,18}|[0-9X]{8,18}?$
帐号是否合法(字母开头，允许 5~16 字节，允许字母数字下划线) : ^[a-zA-Z][a-zA-Z0-9_]{4,15}$
密码 (以字母开头，长度在 6~18 之间，只能包含字母 , 数字和下划线) : ^[a-zA-Z]\w{5,17}$
强密码 (必须包含大小写字母和数字的组合，不能使用特殊字符，长度在 8~10 之间) : ^(?=.*\d)(?=.*[a-z])(?=.*[A-Z]).{8,10}$
日期格式 : ^\d{4}-\d{1,2}-\d{1,2}
一年的 12 个月(01～09和1～12) : ^(0?[1-9]|1[0-2])$
一个月的 31 天(01～09和1～31) : ^((0?[1-9])|((1|2)[0-9])|30|31)$

A.HihoCoder - 1871 Heshen’s Account Book

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
string s[250];
int tot,n;
string ans[maxn];
int cnt[maxn];
regex str("0|([1-9][0-9]*)");

int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    n=0;
    while(getline(cin,s[n]))n++;
    tot=0;
    for(int i=n-1;i>=1;i--){
        while(s[i].size()&&isdigit(s[i][0])&&isdigit(s[i-1].back())){
            s[i-1].push_back(s[i][0]);
            s[i].erase(0,1);
        }
    }
    for(int i=0;i<n;i++){
        stringstream ss;
        ss<<s[i];
        string now;
        while(ss>>now){
            if(regex_match(now,str))ans[tot++]=now,cnt[i]++;
        }
    }
    for(int i=0;i<tot;i++){
        if(i)cout<<" ";
        cout<<ans[i];
    }
    if(tot)cout<<endl;
    for(int i=0;i<n;i++)cout<<cnt[i]<<endl;
    return 0;
}

回文树学习笔记

Diposting di 2019-04-24 | Edited on 2018-10-10

首先，回文树有何功能？
假设我们有一个串S，S下标从0开始，则回文树能做到如下几点：

1.求串S前缀0~i内本质不同回文串的个数（两个串长度不同或者长度相同且至少有一个字符不同便是本质不同）
2.求串S内每一个本质不同回文串出现的次数
3.求串S内回文串的个数（其实就是1和2结合起来）
4.求以下标i结尾的回文串的个数

模板：

const int MAXN = 100005 ;  
const int N = 26 ;  

struct Palindromic_Tree {  
    //cnt最后count一下之后是那个节点代表的回文串出现的次数
    int next[MAXN][N] ;//next指针，next指针和字典树类似，指向的串为当前串两端加上同一个字符构成  
    int fail[MAXN] ;//fail指针，失配后跳转到fail指针指向的节点  
    int cnt[MAXN] ; //表示节点i表示的本质不同的串的个数（建树时求出的不是完全的，最后count()函数跑一遍以后才是正确的） 
    int num[MAXN] ; //表示以节点i表示的最长回文串的最右端点为回文串结尾的回文串个数
    int len[MAXN] ;//len[i]表示节点i表示的回文串的长度（一个节点表示一个回文串）
    int S[MAXN] ;//存放添加的字符  
    int last ;//指向新添加一个字母后所形成的最长回文串表示的节点。
    int n ;//表示添加的字符个数。
    int p ;//表示添加的节点个数。

    int newnode ( int l ) {//新建节点  
        for ( int i = 0 ; i < N ; ++ i ) next[p][i] = 0 ;  
        cnt[p] = 0 ;  
        num[p] = 0 ;  
        len[p] = l ;  
        return p ++ ;  
    }  

    void init () {//初始化  
        p = 0 ;  
        newnode (  0 ) ;  
        newnode ( -1 ) ;  
        last = 0 ;  
        n = 0 ;  
        S[n] = -1 ;//开头放一个字符集中没有的字符，减少特判  
        fail[0] = 1 ;  
    }  

    int get_fail ( int x ) {//和KMP一样，失配后找一个尽量最长的  
        while ( S[n - len[x] - 1] != S[n] ) x = fail[x] ;  
        return x ;  
    }  

    void add ( int c ) {  
        c -= 'a' ;  
        S[++ n] = c ;  
        int cur = get_fail ( last ) ;//通过上一个回文串找这个回文串的匹配位置  
        if ( !next[cur][c] ) {//如果这个回文串没有出现过，说明出现了一个新的本质不同的回文串  
            int now = newnode ( len[cur] + 2 ) ;//新建节点  
            fail[now] = next[get_fail ( fail[cur] )][c] ;//和AC自动机一样建立fail指针，以便失配后跳转  
            next[cur][c] = now ;  
            num[now] = num[fail[now]] + 1 ;  
        }  
        last = next[cur][c] ;  
        cnt[last] ++ ;  
    }  

    void count () {  
        for ( int i = p - 1 ; i >= 0 ; -- i ) cnt[fail[i]] += cnt[i] ;  
        //父亲累加儿子的cnt，因为如果fail[v]=u，则u一定是v的子回文串！  
    }  
} ;

例题1.BZOJ3676

题意

求一个字符串中所有回文子串的出现次数与长度乘积的最大值

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=1e9+7;
const int maxn=3e5+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
const int N=26;
struct PalTree{
    int next[maxn][N];///指向的串威当前串两端加上同一个字符构成
    int fail[maxn];///fail指针，失配后跳转的fail指针指向的结点
    int cnt[maxn];///表示结点i表示的本质不同的串的个数（不全的最后count（）跑一边才是正确的
    int num[maxn];///表示以结点i表示的最长最长回文串的最右端点为为回文结尾的回文串个数
    int len[maxn];///len[i]表示结点i表示的回文串长度
    int S[maxn];///存放添加的字符
    int last;///指向新添加一个字母后形成的最长回文串表示的结点
    int n;///表示添加的字符个数
    int p;///表示添加的结点个数
    int newnode(int l){///新建结点
        for(int i=0;i<N;i++)next[p][i]=0;
        cnt[p]=0;
        num[p]=0;
        len[p]=l;
        return p++;
    }
    void init(){
        p=0;
        newnode(0);
        newnode(-1);
        last=0;
        n=0;
        S[n]=-1;
        fail[0]=1;
    }
    int get_fail(int x){
        while(S[n-len[x]-1]!=S[n])x=fail[x];
        return x;
    }
    void add(int c){
        c-='a';
        S[++n]=c;
        int cur=get_fail(last);///通过上一个回文串找到这个回文串的匹配位置
        if(!next[cur][c]){///如果这个串没出现过，说明出现了一个新的本质不同的回文串
            int now=newnode(len[cur]+2);
            fail[now]=next[get_fail(fail[cur])][c];
            next[cur][c]=now;
            num[now]=num[fail[now]]+1;
        }
        last=next[cur][c];
        cnt[last]++;
    }
    void count(){
        for(int i=p-1;i>=0;i--)cnt[fail[i]]+=cnt[i];
    }
}pat;
char s[maxn];
int main(){
    std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);
    cin>>s;
    int len=strlen(s);
    pat.init();
    for(int i=0;i<len;i++){
        pat.add(s[i]);
    }
    pat.count();
    ll ret=0;
    for(int i=1;i<pat.p;i++){
        ret=max(ll(1LL*pat.len[i]*pat.cnt[i]),ret);
    }
    cout<<ret<<endl;
    return 0;
}

例题2 UVA7041

题意

给出两个仅包含小写字符的字符串 A 和 B ；
求：对于 A 中的每个回文子串，B 中和该子串相同的子串个数的总和。

从0和1两个根节点DFS下去，如果两个相同的节点同时存在就统计答案。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=1e9+7;
const int maxn=4e5+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
const int N=26;
struct PalTree{
    int next[maxn][N];///指向的串威当前串两端加上同一个字符构成
    int fail[maxn];///fail指针，失配后跳转的fail指针指向的结点
    int cnt[maxn];///表示结点i表示的本质不同的串的个数（不全的最后count（）跑一边才是正确的
    int num[maxn];///表示以结点i表示的最长最长回文串的最右端点为为回文结尾的回文串个数
    int len[maxn];///len[i]表示结点i表示的回文串长度
    int S[maxn];///存放添加的字符
    int last;///指向新添加一个字母后形成的最长回文串表示的结点
    int n;///表示添加的字符个数
    int p;///表示添加的结点个数
    int newnode(int l){///新建结点
        for(int i=0;i<N;i++)next[p][i]=0;
        cnt[p]=0;
        num[p]=0;
        len[p]=l;
        return p++;
    }
    void init(){
        p=0;
        newnode(0);
        newnode(-1);
        last=0;
        n=0;
        S[n]=-1;
        fail[0]=1;
    }
    int get_fail(int x){
        while(S[n-len[x]-1]!=S[n])x=fail[x];
        return x;
    }
    void add(int c){
        c-='a';
        S[++n]=c;
        int cur=get_fail(last);///通过上一个回文串找到这个回文串的匹配位置
        if(!next[cur][c]){///如果这个串没出现过，说明出现了一个新的本质不同的回文串
            int now=newnode(len[cur]+2);
            fail[now]=next[get_fail(fail[cur])][c];
            next[cur][c]=now;
            num[now]=num[fail[now]]+1;
        }
        last=next[cur][c];
        cnt[last]++;
    }
    void count(){
        for(int i=p-1;i>=0;i--)cnt[fail[i]]+=cnt[i];
    }
}pat1,pat2;
ll dfs(int a,int b){
    ll ret=0;
    for(int i=0;i<N;i++)if(pat1.next[a][i]!=0&&pat2.next[b][i]!=0)
        ret+=(ll)pat1.cnt[pat1.next[a][i]]*pat2.cnt[pat2.next[b][i]]
        +dfs(pat1.next[a][i],pat2.next[b][i]);
    return ret;
}
char s1[maxn],s2[maxn];
int main(){
    std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);
    int t,cas=0;
    cin>>t;
    while(t--){
        cin>>s1>>s2;
        pat1.init();
        pat2.init();
        int len1=strlen(s1);
        int len2=strlen(s2);
        for(int i=0;i<len1;i++)pat1.add(s1[i]);
        for(int i=0;i<len2;i++)pat2.add(s2[i]);
        pat1.count();pat2.count();
        ll ret=dfs(0,0)+dfs(1,1);
        cout<<"Case #"<<++cas<<": ";
        cout<<ret<<endl;
    }
    return 0;
}

例题3ACM-ICPC 2018 南京赛区网络预赛 Skr

题意

给出一个数字串，求其本质不同的回文子串的和。

在回文树建立的过程中自带去重，所以只需要跑一遍记录答案就好了。

奇根下直接连接的节点所代表的的都是单个字符的回文串，其他都是在两边加上同一个字符，用这个规律去生成数字求和就好了。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=1e9+7;
const int maxn=2e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
const int N=10;
ll modpow(ll a,ll b){
    ll ans=1;
    while(b){
        if(b&1)ans=(ans*a)%mod;
        b>>=1;
        a=(a*a)%mod;
    }
    return ans;
}
struct PalTree{
    int next[maxn][N];///指向的串威当前串两端加上同一个字符构成
    int fail[maxn];///fail指针，失配后跳转的fail指针指向的结点
    int cnt[maxn];///表示结点i表示的本质不同的串的个数（不全的最后count（）跑一边才是正确的
    int num[maxn];///表示以结点i表示的最长最长回文串的最右端点为为回文结尾的回文串个数
    int len[maxn];///len[i]表示结点i表示的回文串长度
    int S[maxn];///存放添加的字符
    int last;///指向新添加一个字母后形成的最长回文串表示的结点
    int n;///表示添加的字符个数
    int p;///表示添加的结点个数
    ll sum[maxn];
    int newnode(int l){///新建结点
        for(int i=0;i<N;i++)next[p][i]=0;
        cnt[p]=0;
        num[p]=0;
        len[p]=l;
        sum[p]=0;
        return p++;
    }
    void init(){
        p=0;
        newnode(0);
        newnode(-1);
        last=0;
        n=0;
        S[n]=-1;
        fail[0]=1;
    }
    int get_fail(int x){
        while(S[n-len[x]-1]!=S[n])x=fail[x];
        return x;
    }
    void add(int c){
        c-='0';
        S[++n]=c;
        int cur=get_fail(last);///通过上一个回文串找到这个回文串的匹配位置
        if(!next[cur][c]){///如果这个串没出现过，说明出现了一个新的本质不同的回文串
            int now=newnode(len[cur]+2);
            fail[now]=next[get_fail(fail[cur])][c];
            next[cur][c]=now;
            num[now]=num[fail[now]]+1;
            sum[now]=(sum[cur]*10*1LL)%mod;
            sum[now]=(sum[now]+c)%mod;
            if(len[cur]>=0)sum[now]=(sum[now]+(c*modpow(10*1LL,len[now]-1))%mod)%mod;
        }
        last=next[cur][c];
        cnt[last]++;
    }
    void count(){
        for(int i=p-1;i>=0;i--)cnt[fail[i]]+=cnt[i];
    }
}pat;

char s[maxn];
int main(){
    std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);
    cin>>s;
    pat.init();
    int len=strlen(s);
    for(int i=0;i<len;i++)pat.add(s[i]);
    ll anw=0;
    for(int i=0;i<pat.p;i++)anw=(anw+pat.sum[i])%mod;
    cout<<anw<<endl;
    return 0;
}

例题4 HIHO#1602 : 本质不同的回文子串的数量

给定一个字符串S，请统计S的所有子串中，有多少个本质不同的回文字符串？

cin>>s;
pat.init();
int len=strlen(s);
for(int i=0;i<len;i++)pat.add(s[i]);
ll anw=0;
pat.count();
cout<<pat.p-2<<endl;
return 0;

牛客小白月赛12

Diposting di 2019-04-24 | Edited on 2019-08-17

A华华听月月唱歌 (贪心)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=1e5+50;
const int inf=1e9;
typedef unsigned long long ull;
int n,m,tot;
struct node{
    int l,r;
}my[maxn];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    cin>>m>>n;
    for(int i=1;i<=n;i++)cin>>my[i].l>>my[i].r;
    sort(my+1,my+1+n,[](node a,node b){
        return a.l<b.l;
    });
    int l=1,k=1;int ans=0;
    while(l<=m&&k<=n){
        int t=0;
        while(my[k].l<=l && k<=n)t=max(my[k].r,t),k++;
        l=t+1;ans++;
        if(t==0)k++;
    }
    if(l>m)cout<<ans<<endl;
    else cout<<-1<<endl;
    return 0;
}

B.华华教月月做数学 (快速幂+龟速乘)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=1e5+50;
const int inf=1e9;
typedef unsigned long long ull;
ll a,b,p;
ll gw(ll a,ll b){
    ll ret=0;
    while(b){
        if(b&1)ret=(ret+a)%p;
        b>>=1;
        a=(a+a)%p;
    }
    return ret;
}
ll pw(ll a,ll b){
    ll ret=1;
    while(b){
        if(b&1)ret=gw(ret,a);
        a=gw(a,a);b>>=1;
    }
    return ret;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int t;
    cin>>t;
    while(t--){
        cin>>a>>b>>p;
        cout<<pw(a,b)<<endl;
    }
    return 0;
}

C.华华给月月出题 (线性筛极性函数)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=2e7+50;
const int inf=1e9;
typedef unsigned long long ull;

ll value[maxn];
bool check[maxn];
ll prime[maxn];

ll pw(ll a,ll n){
    ll ans=1;
    while(n){
        if(n&1)ans=(1LL*ans*a)%mod;
        a=(a*a)%mod;
        n>>=1;
    }
    return ans;
}
ll getvalue(ll n){
    value[1]=1;
    int tot=0;
    for(ll i=2;i<=n;i++){
        if(!check[i]){
            value[i]=1LL*pw(1LL*i,1LL*n);
            prime[tot++]=i;
        }
        for(ll j=0;j<tot;j++){
            if(1LL*i*prime[j]>n)break;
            check[i*prime[j]]=true;
            value[i*prime[j]]=1LL*value[i]*value[prime[j]]%mod;
            if(i%prime[j]==0)break;
           /* else{
                value[i*prime[j]]=1LL*value[i]*value[prime[j]]%mod;
            }*/
        }
    }
    ll ans=0;
    for(int i=1;i<=n;i++)ans=(1LL*ans^value[i]);
    return ans;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    ll n;
    cin>>n;
    cout<<getvalue(n);
    return 0;
}

D.月月给华华出题 (线性筛欧拉函数)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=1e6+50;
const int inf=1e9;
typedef unsigned long long ull;
bool check[maxn];
int phi[maxn];
int prime[maxn];
int tot;
void phi_and_prime_table(int N){
    phi[1]=1;
    for(int i=2;i<=N;i++){
        if(!check[i]){
            prime[tot++]=i;
            phi[i]=i-1;
        }
        for(int j=0;j<tot;j++){
            if(i*prime[j]>N)break;
            check[i*prime[j]]=true;
            if(i%prime[j]==0){
                phi[i*prime[j]]=phi[i]*prime[j];
                break;
            }
            else{
                phi[i*prime[j]]=phi[i]*(prime[j]-1);
            }
        }
    }

}
ll ans[maxn];
ll cal(int n){
    return 1LL*n*phi[n]/2+(n==1);
}
int main()
{
    /*std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);*/
    int n;
    scanf("%d",&n);
    phi_and_prime_table(n);
    for(int i=1;i<=n;i++){
        for(int j=i;j<=n;j+=i)ans[j]+=cal(j/i);
    }
    for(int i=1;i<=n;i++)
        printf("%lld\n",ans[i]);
    return 0;
}

E.华华给月月准备礼物 (二分)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=2e5+50;
const int inf=1e9;
typedef unsigned long long ull;
int a[maxn];
int n,k;
bool ok(int mid){
    int ans=0;
    for(int i=1;i<=n;i++){
        ans+=a[i]/mid;
    }
    if(ans>=k)return true;
    else return false;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    cin>>n>>k;
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    int l=1,r=1e9+1,ans=0;
    while(l<=r){
        int mid=(l+r)/2;
        if(ok(mid)){
            ans=mid,l=mid+1;
        }
        else r=mid-1;
    }
    cout<<ans<<endl;
    return 0;
}

F.华华开始学信息学 (分类讨论+树状数组)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=1e5+50;
const int inf=1e9;
typedef unsigned long long ull;

ll lazy[maxn];
ll sum[maxn];
int block;
void update(int x,int val){
    while(x<maxn){
        sum[x]+=val;
        x+=(x&(-x));
    }
}
ll query(int x){
    ll ans=0;
    while(x){
        ans+=sum[x];
        x-=(x&(-x));
    }
    return ans;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n,m;
    cin>>n>>m;
    block=sqrt(n);
    int op,a,b;
    while(m--){
        cin>>op>>a>>b;
        if(op==1){
            if(a>block){
                for(int i=a;i<=n;i+=a)update(i,b);
            }
            else lazy[a]+=b;
        }
        else{
            ll ans=query(b)-query(a-1);
            for(int i=1;i<=block;i++){
                ans+=(b/i-(a-1)/i)*lazy[i];
            }
            cout<<ans<<endl;
        }
    }
    return 0;
}

G.华华对月月的忠诚 (思维)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=1e5+50;
const int inf=1e9;
typedef unsigned long long ull;


int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    ll a,b;
    string n;
    cin>>a>>b>>n;
    cout<<__gcd(a,b);

    return 0;
}

H.华华和月月种树 (树状数组)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=5e5+50;
const int inf=1e9;
typedef unsigned long long ull;

ll sum[maxn],cnt,sz[maxn],id[maxn];
void update(int x,int val){
    while(x<maxn){
        sum[x]+=val;
        x+=(x&(-x));
    }
}
ll query(int x){
    ll ans=0;
    while(x){
        ans+=sum[x];
        x-=(x&(-x));
    }
    return ans;
}
struct node{
    int a,b,c;
}my[maxn];
vector<int>G[maxn];
void add(int u,int v){
    G[u].push_back(v);
    G[v].push_back(u);
}
void dfs(int now,int pre){
    sz[now]=1;
    id[now]=++cnt;
    for(auto i:G[now]){
        if(i==pre)continue;
        dfs(i,now);
        sz[now]+=sz[i];
    }
}
int n;
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int m;
    cin>>m;
    for(int i=1;i<=m;i++){
        cin>>my[i].a>>my[i].b;
        if(my[i].a==1){
            n++;
            add(my[i].b,n);
        }
        if(my[i].a==2)cin>>my[i].c;
    }
    dfs(0,-1);
    int res=0;
    for(int i=1;i<=m;i++){
        if(my[i].a==1){
            res++;
            int x=query(id[res]);
            update(id[res],-x);
            update(id[res]+sz[res],x);
        }
        else if(my[i].a==2){
            update(id[my[i].b],my[i].c);
            update(id[my[i].b]+sz[my[i].b],-my[i].c);
        }
        else cout<<query(id[my[i].b])<<endl;
    }
    return 0;
}

I.华华和月月逛公园 (求桥)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=1e5+50;
const int inf=1e9;
typedef unsigned long long ull;

struct Edge{
    int u,v;
};
///割顶 bccno 无意义
int pre[maxn],iscut[maxn],bccno[maxn],dfs_clock,bcc_cut;
vector<int>G[maxn],bcc[maxn];
stack<Edge>S;
void init(int n){
    for (int i = 0; i < n; i++) G[i].clear();
}
int lowu[maxn];
int father[maxn];
inline void add_edge(int u, int v) { G[u].push_back(v), G[v].push_back(u); }
void dfs(int u,int fa){
    lowu[u] = pre[u] = dfs_clock++;
    father[u]=fa;
    int child = 0;
    for(int i = 0; i < G[u].size(); i++){
        int v =G[u][i];
        if(pre[v]==-1){
            dfs(v,u);
            lowu[u]=min(lowu[u],lowu[v]);
        }
        else if(v!=fa){
            lowu[u]=min(lowu[u],pre[v]);
        }
    }
}

int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=m;i++){
        int u,v;
        cin>>u>>v;
        add_edge(u,v);
    }
    memset(pre,-1,sizeof(pre));
    memset(lowu,-1,sizeof(lowu));
    dfs(1,-0);
    int sum=0;
    for(int i=1;i<=n;i++){
        int v=father[i];
        if(v>0&&lowu[i]>pre[v])sum++;
    }
    cout<<m-sum<<endl;
    return 0;
}

J. 月月查华华的手机 (贪心)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=1e6+50;
const int inf=1e9;
typedef unsigned long long ull;
int go[maxn][30];
char s[maxn];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    cin>>s;
    int len=strlen(s);
    for(int i=0;i<26;i++){
        go[len][i]=-1;
    }
    for(int i=len-1;i>=0;i--){
        for(int j=0;j<26;j++){
            if(s[i]==char('a'+j)){
                go[i][j]=i+1;
            }
            else
                go[i][j]=go[i+1][j];
        }
    }
   /* for(int i=0;i<26;i++){
        cout<<char('a'+i)<<" ";
    }
    cout<<endl;
    for(int i=0;i<=len;i++){
        for(int j=0;j<26;j++){
            cout<<go[i][j]<<" ";
        }
        cout<<endl;
    }*/
    int m;
    cin>>m;
    while(m--){
        cin>>s;
        len=strlen(s);
        int now=0,flag=0;
        for(int i=0;i<len;i++){
            now=go[now][s[i]-'a'];
            if(now==-1){
                flag=1;break;
            }
          //  cout<<"i="<<i<<" now="<<now<<endl;
        }
        if(flag)cout<<"No"<<endl;
        else cout<<"Yes"<<endl;
    }
    return 0;
}

网络流学习笔记

Diposting di 2019-04-24 | Edited on 2019-02-05

学习自https://blog.csdn.net/txl199106/article/details/64441994

一.网络流:流&网络&割

1.网络流问题(NetWork Flow Problem):

给定指定的一个有向图,其中有两个特殊的点源S(Sources)和汇T(Sinks),每条边有指定的容量(Capacity),求满足条件的从S到T的最大流(MaxFlow).

下面给出一个通俗点的解释
(下文基本避开形式化的证明基本都用此类描述叙述)
好比你家是汇自来水厂(有需要的同学可以把自来水厂当成银行之类以下类似)是源
然后自来水厂和你家之间修了很多条水管子接在一起水管子规格不一有的容量大有的容量小
然后问自来水厂开闸放水你家收到水的最大流量是多少
如果自来水厂停水了你家那的流量就是0 当然不是最大的流量

但是你给自来水厂交了100w美金自来水厂拼命水管里通水但是你家的流量也就那么多不变了这时就达到了最大流

2.三个基本的性质:

如果 C代表每条边的容量 F代表每条边的流量
一个显然的实事是F小于等于C 不然水管子就爆了，这就是网络流的第一条性质容量限制(Capacity Constraints):F ≤ C
再考虑节点任意一个节点流入量总是等于流出的量否则就会蓄水(爆炸危险…)或者平白无故多出水(有地下水涌出?)
这是第二条性质流量守恒(Flow Conservation):Σ F = Σ F
当然源和汇不用满足流量守恒我们不用去关心自来水厂的水是河里的还是江里的
最后一个不是很显然的性质是斜对称性(Skew Symmetry): F = - F
这其实是完善的网络流理论不可缺少的就好比中学物理里用正负数来定义一维的位移一样
百米起点到百米终点的位移是100m的话那么终点到起点的位移就是-100m
同样的 x向y流了F的流 y就向x流了-F的流

对于任意一个时刻，设f(u,v)实际流量，则整个图G的流网络满足3个性质：

容量限制：对任意u,v∈V，f(u,v)≤c(u,v)。
反对称性：对任意u,v∈V，f(u,v) = -f(v,u)。从u到v的流量一定是从v到u的流量的相反值。
流守恒性：对任意u，若u不为S或T，一定有∑f(u,v)=0，(u,v)∈E。即u到相邻节点的流量之和为0，因为流入u的流量和u点流出的流量相等，u点本身不会”制造”和”消耗”流量。

3.容量网络&流量网络&残留网络:

网络就是有源汇的有向图关于什么就是指边权的含义是什么
容量网络就是关于容量的网络基本是不改变的(极少数问题需要变动)

流量网络就是关于流量的网络在求解问题的过程中
通常在不断的改变但是总是满足上述三个性质
调整到最后就是最大流网络同时也可以得到最大流值

残留网络往往概括了容量网络和流量网络是最为常用的
残留网络=容量网络-流量网络
这个等式是始终成立的残留值当流量值为负时甚至会大于容量值
流量值为什么会为负?有正必有负,记住斜对称性!

4.割&割集:

无向图的割集(Cut Set):C[A,B]是将图G分为A和B两个点集 A和B之间的边的全集
网络的割集:C[S,T]是将网络G分为s和t两部分点集 S属于s且T属于t 从S到T的边的全集
带权图的割(Cut)就是割集中边或者有向边的权和

通俗的理解一下:
割集好比是一个恐怖分子把你家和自来水厂之间的水管网络砍断了一些
然后自来水厂无论怎么放水水都只能从水管断口哗哗流走了你家就停水了
割的大小应该是恐怖分子应该关心的事毕竟细管子好割一些

而最小割花的力气最小

二.计算最大流的基本算法

那么怎么求出一个网络的最大流呢?
这里介绍一个最简单的算法:

Edmonds-Karp算法即最短路径增广算法简称EK算法

EK算法基于一个基本的方法:Ford-Fulkerson方法即增广路方法简称FF方法
增广路方法是很多网络流算法的基础一般都在残留网络中实现
其思路是每次找出一条从源到汇的能够增加流的路径调整流值和残留网络不断调整直到没有增广路为止
FF方法的基础是增广路定理(Augmenting Path Theorem):网络达到最大流当且仅当残留网络中没有增广路
证明略这个定理应该能够接受的吧
EK算法就是不断的找最短路找的方法就是每次找一条边数最少的增广也就是最短路径增广

这样就产生了三个问题:

1.最多要增广多少次?

可以证明最多O(VE)次增广可以达到最大流证明略

2.如何找到一条增广路?

先明确什么是增广路增广路是这样一条从s到t的路径路径上每条边残留容量都为正
把残留容量为正的边设为可行的边那么我们就可以用简单的BFS得到边数最少的增广路

.如何增广?

BFS得到增广路之后这条增广路能够增广的流值是路径上最小残留容量边决定的
把这个最小残留容量MinCap值加到最大流值Flow上同时路径上每条边的残留容量值减去MinCap
最后路径上每条边的反向边残留容量值要加上MinCap 为什么? 下面会具体解释

这样每次增广的复杂度为O(E) EK算法的总复杂度就是O(VE^2)，事实上大多数网络的增广次数很少 EK算法能处理绝大多数问题，平均意义下增广路算法都是很快的
增广路算法好比是自来水公司不断的往水管网里一条一条的通水
上面还遗留了一个反向边的问题: 为什么增广路径上每条边的反向边残留容量值要加上MinCap?

因为斜对称性! 由于残留网络=容量网络-流量网络
容量网络不改变的情况下
由于增广好比给增广路上通了一条流路径说所有边流量加MinCap
流量网络中路径上边的流量加MinCap 反向边流量减去MinCap
相对应的残留网络就发生相反的改变

这样我们就完成了EK算法具体实现可以用邻接表存图也可以用邻接矩阵存图
邻接表存图由于流量同时存在于边与反向边为了方便求取反向边建图把一对互为反向边的边建在一起
代码很简单最好自己实现一下

看一个具体的增广路算法的例子吧

=====================================================================

三.最大流最小割定理

下面介绍网络流理论中一个最为重要的定理
最大流最小割定理(Maximum Flow, Minimum Cut Theorem):网络的最大流等于最小割
具体的证明分三部分

1.任意一个流都小于等于任意一个割

这个很好理解自来水公司随便给你家通点水构成一个流
恐怖分子随便砍几刀砍出一个割
由于容量限制每一根的被砍的水管子流出的水流量都小于管子的容量
每一根被砍的水管的水本来都要到你家的现在流到外面加起来得到的流量还是等于原来的流
管子的容量加起来就是割所以流小于等于割
由于上面的流和割都是任意构造的所以任意一个流小于任意一个割

2.构造出一个流等于一个割

当达到最大流时根据增广路定理
残留网络中s到t已经没有通路了否则还能继续增广
我们把s能到的的点集设为S 不能到的点集为T
构造出一个割集C[S,T] S到T的边必然满流否则就能继续增广
这些满流边的流量和就是当前的流即最大流
把这些满流边作为割就构造出了一个和最大流相等的割

3.最大流等于最小割

设相等的流和割分别为Fm和Cm
则因为任意一个流小于等于任意一个割
任意F≤Fm=Cm≤任意C
定理说明完成，证明如下：

对于一个网络流图G=(V,E)，其中有源点s和汇点t，那么下面三个条件是等价的：
1. 流f是图G的最大流
2. 残留网络Gf不存在增广路
3. 对于G的某一个割(S,T)，此时f = C(S,T)

首先证明1 => 2：

1	我们利用反证法，假设流f是图G的最大流，但是残留网络中还存在有增广路p，其流量为fp。则我们有流f'=f+fp>f。这与f是最大流产生矛盾。

接着证明2 => 3：

1
2
3

假设残留网络Gf不存在增广路，所以在残留网络Gf中不存在路径从s到达t。我们定义S集合为：当前残留网络中s能够到达的点。同时定义T=V-S。
此时(S,T)构成一个割(S,T)。且对于任意的u∈S,v∈T，有f(u,v)=c(u,v)。若f(u,v)<c(u,v)，则有Gf(u,v)>0，s可以到达v，与v属于T矛盾。
因此有f(S,T)=Σf(u,v)=Σc(u,v)=C(S,T)。

最后证明3 => 1：

1
2

由于f的上界为最小割，当f到达割的容量时，显然就已经到达最大值，因此f为最大流。
这样就说明了为什么找不到增广路时，所求得的一定是最大流。

最大流

最大流相关算法有两种解决思想, 一种是增广路算法思想, 另一种是预流推进算法思想。下面将分别介绍这两种算法思想。

增广路算法(Ford-Fulkerson)

基本思想

根据增广路定理, 为了得到最大流, 可以从任何一个可行流开始, 沿着增广路对网络流进行增广, 直到网络中不存在增广路为止,这样的算法称为增广路算法。问题的关键在于如何有效地找到增广路, 并保证算法在有限次增广后一定终止。
增广路算法的基本流程是 :

(1) 取一个可行流 f 作为初始流(如果没有给定初始流,则取零流 f= { 0 }作为初始流);
(2) 寻找关于 f 的增广路 P,如果找到,则沿着这条增广路 P 将 f 改进成一个更大的流, 并建立相应的反向弧;
(3) 重复第(2)步直到 f 不存在增广路为止。

图示如下:

增广路算法的关键是寻找增广路和改进网络流。
问题: 为什么要创建反向弧呢?
原因: 为程序提供一次反悔的机会什么意思, 如下图所示:
在图中如果程序找到了一条增广路 1 -> 2 -> 4 -> 6, 此时得到一个流量为 2 的流并且无法继续进行增广,
但是如果在更新可行流的同时建立反向弧的话, 就可以找到 1 -> 3 -> 4 -> 2 -> 5 -> 6 的可行流, 流量为1, 这样就可以得到最大流为 3.

一般增广路算法(EdmondsKarp)

算法流程

在一般的增广路算法中, 程序的实现过程与增广路求最大流的过程基本一致. 即每一次更新都进行一次找增广路然后更新路径上的流量的过程。但是我们可以从上图中发现一个问题, 就是每次找到的增广路曲曲折折非常长, 此时我们往往走了冤枉路(即：明明我们可以从源点离汇点越走越进的，可是中间的几条边却向离汇点远的方向走了), 此时更新增广路的复杂度就会增加。EK 算法为了规避这个问题使用了 bfs 来寻找增广路, 然后在寻找增广路的时候总是向离汇点越来越近的方向去寻找下一个结点。

算法实现

邻接矩阵

#include <queue>
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
const int MAXN = 300;
const int MAX_INT = ((1 << 31) - 1);
 
int n;                                      // 图中点的数目
int pre[MAXN];                              // 从 s - t 中的一个可行流中, 节点 i 的前序节点为 Pre[i];
bool vis[MAXN];                             // 标记一个点是否被访问过
int mp[MAXN][MAXN];                         // 记录图信息
 
bool bfs(int s, int t){
    queue <int> que;
    memset(vis, 0, sizeof(vis));
    memset(pre, -1, sizeof(pre));
    pre[s] = s;
    vis[s] = true;
    que.push(s);
    while(!que.empty()){
        int u = que.front();
        que.pop();
        for(int i = 1; i <= n; i++){
            if(mp[u][i] && !vis[i]){
                pre[i] = u;
                vis[i] = true;
                if(i == t) return true;
                que.push(i);
            }
        }
    }
    return false;
}
 
int EK(int s, int t){
    int ans = 0;
    while(bfs(s, t)){
        int mi = MAX_INT;
        for(int i = t; i != s; i = pre[i]){
            mi = min(mi, mp[pre[i]][i]);
        }
        for(int i = t; i != s; i = pre[i]){
            mp[pre[i]][i] -= mi;
            mp[i][pre[i]] += mi;
        }
        ans += mi;
    }
    return ans;
}

邻接表

const int MAXN = 430;
const int MAX_INT = (1 << 30);
 
struct Edge{
    int v, nxt, w;
};
 
struct Node{
    int v, id;
};
 
int n, m, ecnt;
bool vis[MAXN];
int head[MAXN];
Node pre[MAXN];
Edge edge[MAXN];
 
void init(){
    ecnt = 0;
    memset(edge, 0, sizeof(edge));
    memset(head, -1, sizeof(head));
}
 
void addEdge(int u, int v, int w){
    edge[ecnt].v = v;
    edge[ecnt].w = w;
    edge[ecnt].nxt = head[u];
    head[u] = ecnt++;
}
 
bool bfs(int s, int t){
    queue <int> que;
    memset(vis, 0, sizeof(vis));
    memset(pre, -1, sizeof(pre));
    pre[s].v = s;
    vis[s] = true;
    que.push(s);
    while(!que.empty()){
        int u = que.front();
        que.pop();
        for(int i = head[u]; i + 1; i = edge[i].nxt){
            int v = edge[i].v;
            if(!vis[v] && edge[i].w){
                pre[v].v = u;
                pre[v].id = i;
                vis[v] = true;
                if(v == t) return true;
                que.push(v);
            }
        }
    }
    return false;
}
 
int EK(int s, int t){
    int ans = 0;
    while(bfs(s, t)){
        int mi = MAX_INT;
        for(int i = t; i != s; i = pre[i].v){
            mi = min(mi, edge[pre[i].id].w);
        }
        for(int i = t; i != s; i = pre[i].v){
            edge[pre[i].id].w -= mi;
            edge[pre[i].id ^ 1].w += mi;
        }
        ans += mi;
    }
    return ans;
}
 
// 加边
addEdge(u, v, w);
addEdge(v, u, 0);
// 调用
int ans = EK(s, t);

算法复杂度

每进行一次增广需要的时间复杂度为 bfs 的复杂度 + 更新残余网络的复杂度, 大约为 O(m)(m为图中的边的数目), 需要进行多少次增广呢, 假设每次增广只增加1, 则需要增广 nW 次(n为图中顶点的数目, W为图中边上的最大容量), .

Dinic算法

算法思想

DINIC 在找增广路的时候也是找的最短增广路, 与 EK 算法不同的是 DINIC 算法并不是每次 bfs 只找一个增广路, 他会首先通过一次 bfs 为所有点添加一个标号, 构成一个 层次图，然后在层次图中寻找增广路进行更新。

算法流程

1
2
3

1.利用 BFS 对原来的图进行分层，即对每个结点进行标号， 这个标号的含义是当前结点距离源点的最短距离(假设每条边的距离都为1)，注意：构建层次图的时候所走的边的残余流量必须大于0
2.用 DFS 寻找一条从源点到汇点的增广路, 注意: 此处寻找增广路的时候要按照层次图的顺序, 即如果将边(u, v)纳入这条增广路的话必须满足dis[u]=dis[v]−1, 其中 dis[i]为结点 ii的编号。找到一条路后要根据这条增广路径上的所有边的残余流量的最小值ll更新所有边的残余流量(即正向弧 - l, 反向弧 + l).
3.重复步骤 2, 当找不到一条增广路的时候, 重复步骤 1, 重新建立层次图, 直到从源点不能到达汇点为止。

算法实现

#include <queue>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int MAXN = 510;
const int MAXN_INT = (1 << 29);
 
int n, m;
int dis[MAXN];
int mp[MAXN][MAXN];
 
int bfs(int s){
    memset(dis, 0xff, sizeof(dis));
    dis[s] = 0;
    queue <int> que;
    que.push(s);
    while(!que.empty()){
        int top = que.front();
        que.pop();
        for(int i = 1; i <= n; i++){
            if(dis[i] < 0 && mp[top][i] > 0){
                dis[i] = dis[top] + 1;
                que.push(i);
            }
        }
    }
    if(dis[n] > 0) return true;
    return false;
}
 
int Find(int x, int low){
    int a = 0;
    if(x == n) return low;
    for(int i = 1; i <= n; i++){
        if(mp[x][i] > 0 
            && dis[i] == dis[x] + 1
            && (a = Find(i, min(low, mp[x][i])))){
            mp[x][i] -= a;
            mp[i][x] += a;
            return a;
        }
    }
    return 0;
}
 
int main(){
    while(scanf("%d%d", &n, &m) != EOF){
        memset(mp, 0, sizeof(mp));
        int u, v, w;
        for(int i = 0; i < m; i++){
            scanf("%d%d%d", &u, &v, &w);
            mp[u][v] += w;
        }
        int ans = 0, tmp;
        while(bfs(1)){
            while(tmp = Find(1, MAXN_INT))
                ans += tmp;
        }
        printf("%d\n", ans);
    }
    return 0;
}

当前弧优化和多路增广

#include <queue>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int MAXN = 101000;
const int MAXN_INT = (1 << 29);
 
struct Edge{
    int v, w, nxt;
};
 
int s, t;
int n, m, ecnt;
Edge edge[MAXN * 2];
int head[MAXN], dis[MAXN], curEdge[MAXN];
 
void init(){
    ecnt = 0;
    memset(dis, -1, sizeof(dis));
    memset(edge, 0, sizeof(edge));
    memset(head, -1, sizeof(head));
}
 
void addEdge(int u, int v, int w){
    edge[ecnt].v = v;
    edge[ecnt].w = w;
    edge[ecnt].nxt = head[u];
    head[u] = ecnt++;
}
 
int bfs(){
    memset(dis,-1,sizeof(dis));
    dis[t] = 0;
    queue <int> que;
    que.push(t);
    while(!que.empty()){
        int u = que.front();
        que.pop();
        for(int i = head[u]; i + 1; i = edge[i].nxt){
            if(dis[edge[i].v] == -1 && edge[i ^ 1].w > 0){
                dis[edge[i].v] = dis[u] + 1;
                que.push(edge[i].v);
            }
        }
    }
    return dis[s] != -1;
}
 
int dfs(int u, int v, int flow){
    if(u == t) return flow;
    int delta = flow;
    for(int &i = curEdge[u]; i + 1; i = edge[i].nxt){
        if(dis[u] == dis[edge[i].v] + 1 && edge[i].w){
            int d = dfs(edge[i].v, v, min(delta, edge[i].w));
            edge[i].w -= d, edge[i ^ 1].w += d;
            delta -= d;
            if(delta == 0) break;
        }
    }
    return flow - delta;
}
 
int dinic(){
    int ans = 0;
    while(bfs()){
        for(int i = 0; i < n; i++)
            curEdge[i] = head[i];
        ans += dfs(s, t, MAXN_INT);
    }
    return ans;
}
 
int main(){
    while(scanf("%d%d", &n, &m) != EOF){
        init();
        int u, v, w;
        for(int i = 0; i < m; i++){
            scanf("%d%d%d", &u, &v, &w);
            addEdge(u, v, w);
            addEdge(v, u, 0);
        }
        printf("%d\n", dinic());
    }
    return 0;
}

时间复杂度

$O(V^2E)

最短增广路算法(SAP)

算法思想

最短增广路算法是一种运用距离标号使寻找增广路的时间复杂度下降的算法。所谓的距离标号就是某个点到汇点的最少的弧的数量(即当边权为1时某个点的最短路径长度). 设点i的标号为d[i], 那么如果将满足d[i] = d[j] + 1, 且增广时只走允许弧, 那么就可以达到”怎么走都是最短路”的效果. 每个点的初始标号可以在一开始用一次从汇点沿所有反向的BFS求出.

算法流程

1) 定义节点的标号为到汇点的最短距离;
2) 每次沿可行边进行增广, 可行边即: 假设有两个点 i, j 若 d[i] = 3, d[j] = 4, 则d[j] = d[i] + 1, 也就是从 j 到 i 有一条边.
3) 找到增广路后，将路径上所有边的流量更新.
4) 遍历完当前结点的可行边后更新当前结点的标号为 d[now]=min(d[next]|Flow(now,next)>0)+1，使下次再搜的时候有路可走。
5) 图中不存在增广路后即退出程序，此时得到的流量值就是最大流。

需要注意的是, 标号的更新过程首先我们要理解更新标号的目的。标号如果需要更新，说明在当前的标号下已经没有增广路可以继续走，这时更新标号就可以使得我们有继续向下走的可能，并且每次找的都是能走到的点中标号最小的那个点，这样也使得每次搜索长度最小.
下面的图演示了标号的更新过程:

1.首先我们假设有个图如下，为了简化没有标箭头也没有写流量:

2.为图标号, 每个点的标号为其到汇点的最短距离(这里把每条边看作1)

3.第一遍遍历时，找到了1->2->9这样一条增广路以后，更新边上流量值, 得到下图
棕色字体为边上的流量值。这时按照标号再搜一遍,发现从1出发已经找不到增广路了，因为flow(1,2)等于0不可以走，h[1]=2,h[3]=2≠h[1]+1,h[5]=4≠h[1]+1，所以这时更新1的标号，
4.按照 min(h[next]|Flow(now,next)>0)+1，修改后 h[1]=h[3]+1=3.

5.第二遍遍历以后找到了这样一条增广路：1->3->4->9,做完这条路以后又发现无法找到可行边了，这时再更新标号使图中有路可走，如上文所说的那样做，再次修改后h[1]=h[5]+1=5h[1]=h[5]+1=5，就这样搜索并更新直到变成下图

6.这时再更新h[1]发现没有点可以用来更新h[1]了，于是此时h[1]=∞，使程序退出。

GAP 优化: 由于可行边定义为：(now,next)|h[now]=h[next]+1，所以若标号出现“断层”即有的标号对应的顶点个数为0，则说明剩余图中不存在增广路，此时便可以直接退出，降低了无效搜索。举个栗子：若结点标号为3的结点个数为0，而标号为4的结点和标号为2的结点都大于 0,那么在搜索至任意一个标号为4的结点时，便无法再继续往下搜索，说明图中就不存在增广路。此时我们可以以将h[1]=n 形式来变相地直接结束搜索

算法实现

#include <queue>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int MAXN = 5010;
const int MAXN_INT = (1 << 29);
 
struct Edge{
    int v, w, nxt;
};
 
bool isFind;
int head[MAXN];
Edge edge[MAXN];
int dis[MAXN], gap[MAXN];
int n, m, ecnt, aug, maxFlow;
 
 
void init(){
    ecnt = maxFlow = 0;
    memset(gap, 0, sizeof(gap));
    memset(dis, 0, sizeof(dis));
    memset(edge, 0, sizeof(edge));
    memset(head, -1, sizeof(head));
    gap[0] = n;
}
 
void addEdge(int u, int v, int w){
    edge[ecnt].v = v;
    edge[ecnt].w = w;
    edge[ecnt].nxt = head[u];
    head[u] = ecnt++;
}
 
void Find(int s){
    int dx, augc, minDis;
    if(s == n){
        isFind = true;
        maxFlow += aug;
        return;
    }
 
    augc = aug;
    minDis = n - 1;
    for(int i = head[i]; i + 1; i = edge[i].nxt){
        if(edge[i].w > 0){
            if(dis[s] == dis[edge[i].v] + 1){
                aug = min(aug, edge[i].w);
                Find(edge[i].v);
                if(dis[1] >= n) return;
                if(isFind){
                    dx = i;
                    break;
                }
                aug = augc;
            }
            minDis = min(minDis, dis[edge[i].v]);
        }
    }
    if(!isFind){
        gap[dis[s]]--;
        if(gap[dis[s]] == 0) dis[1] = n;
        dis[s] = minDis + 1;
        gap[dis[s]]++;
    }else{
        edge[dx].w -= aug;
        edge[dx ^ 1].w += aug;
    }
}
 
int main(){
    while(scanf("%d%d", &n, &m) != EOF){
        init();
        int u, v, w;
        for(int i = 0; i < m; i++){
            scanf("%d%d%d", &u, &v, &w);
            addEdge(u, v, w);
            addEdge(v, u, 0);
        }
 
        while(dis[1] < n){
            isFind = 0;
            aug = MAXN_INT;
            Find(1);
        }
        cout << maxFlow << endl;
    }
    return 0;
}

算法复杂度

O(V^2 E)

预流推进算法

算法思想

预流推进算法是从一个预流出发对活跃顶点沿着允许弧进行流量增广,每次增广称为一次推进。在推进过程中,流一定满足流量限制条件,但一般不满足流量平衡条件, 因此只是一个伪流。此外, 如果一个伪流中, 从每个顶点(除源点 V s 、汇点 V t 外)流出的流量之和总是小于等于流入该顶点的流量之和, 称这样的伪流为预流。因此这类算法被称为预流推进算法。

算法流程

1.首先用一边 BFS 为图中每个顶点一个标号dis[v], 表示该点到v的最短路.
2.将与 S 相连的边设为满流, 并将这时产生的活动结点加入队列Q。
3.选出 Q 的一个活动结点 u 并依次判断残量网咯 G’ 中每条边(u, v), 若 dis[u]=min(dis[v]+1) 则顺着这些边推流, 直到 Q 变成非活动结点(不存在多余流量).
4.如果 u 还是活动结点，则需要对 u 进行重新标号: dis[u]=min(dis[v]+1), 其中边 (u, v) 存在于 G’ 中,然后再将 u 加入队列。
5.重复3, 4两个步骤直到队列 Q 为空。

算法实现

const int size = 501;
const int MAX = 1 << 15;
 
int graph[size][size];
int label[size];        //标号
bool visited[size];
 
bool bfs(int st, int ed)
{
    memset(label, -1, sizeof(label));
    memset(visited, false, sizeof(visited));
    label[st] = 0;
    visited[st] = true;
    vector < int >plist;
    plist.push_back(st);
    while (plist.size()) {
    int p = plist[0];
    plist.erase(plist.begin());
    for (int i = 0; i < size; i++) {
        if (graph[i][p] > 0 && !visited[i]) {
        plist.push_back(i);
        visited[i] = true;
        label[i] = label[p] + 1;
        }
    }
    }
    if (label[ed] == -1) {
    return false;
    }
    return true;
}
 
int inflow[size];       //流入量
 
int maxFlow()
{
    memset(inflow, 0, sizeof(inflow));
 
    //hights
    bfs(size - 1, 0);       //end point: size - 1, start point: 0
    memset(visited, false, sizeof(visited));
 
//prepare()
    vector < int >plist;
    for (int i = 0; i < size; i++) {
    if (graph[start][i] > 0) {
        inflow[i] = graph[start][i];
        graph[start][i] -= inflow[i];
        graph[i][start] += inflow[i];
        if (!visited[i]) {
        plist.push_back(i);
        visited[i] = true;
        }
    }
    }
    while (plist.size()) {
    int p = plist[0];
    plist.erase(plist.begin());
    visited[p] = false;
    int minLabel = -1;
    for (int i = 0; i < size; i++) {
        if (graph[p][i] > 0) {
        if (label[p] == label[i] + 1) {
            int flow = min(inflow[p], graph[p][i]);
            inflow[p] -= flow;
            inflow[i] += flow;
            graph[p][i] -= flow;
            graph[i][p] += flow;
 
            if (!visited[i] && inflow[i] > 0) {
            plist.push_back(i);
            visited[i] = true;
            }
        }
        }
    }
    if (inflow[p] > 0 && p != end) {
        for (int i = 0; i < size; i++) {
        if (graph[p][i] > 0) {
            if (minLabel == -1 || minLabel > label[i] + 1) {
            minLabel = label[i] + 1;
            }
        }
        }
        if (!visited[p] && minLabel != -1 && minLabel < size)    //minLabel < size, 这个条件需要加上, 因为经过测试发现有死循环的可能
        {
        for (int i = 0; i < size; i++) {
            if (label[i] + 1 == minLabel && graph[p][i] > 0) {
            visited[p] = true;
            label[p] = minLabel;
            plist.push_back(p);
            break;
            }
        }
        }
    }
    }
    return inflow[end];
}

算法复杂度

如果该算法的Q是标准的FIFO队列，则时间复杂度为(n2m)，最高标号不会超过n（超过时必无到汇的路径），所以n个点每个最多重新标号n次，两次标号之间m条边每条最多推流一次。如果是优先队列，并且标号最高的点优先的话，我们就得到了最高标号预流推进算法，其时间复杂度仅为n2m−−√.

最小费用最大流

简介

最小费用最大流是解决这么一种问题: 对于图中的每一条边来说, 除了有一个最大容量的属性以外，还有一个费用属性, 即流过这条边的单位流量的花费。求解的问题为在保证从源点到汇点的流量最大的前提下使得花费最少。

求解思想

我们来考虑这么一个问题: 在最短路的一些变形的题目中往往有这种题，每条路不仅仅有一个长度还有一个建设的费用，最终求从起点到终点在保证路最短的前提下，使得花费的钱最少。当时我们是怎么求解的呢？
首先我们知道，最短路的长度是一定的，但是组成一条最短路的边是不一定的，所以我们在搜索这条最短路的时候只要通过调整待选边的优先级来控制搜索的方向就可以满足上述问题的要求。
这个问题跟我们现在求解的最小费用最大流问题神似啊，只要我们在寻找增广路的时候调整待选边的优先级来控制寻找方向，这个问题就可以解决了啊。我们直到对于一条增广路来说, 花费满足: cost=minFlow∗∑wi(i∈增广路上的边), 实际上这里的优先级就是每条边的长度认为是其单位流量的花费的最短路。

求解算法

基于最大流的三种算法，求解最小费用最大流也具有三种算法，我们来对比一下这三对算法:

最大流 EK 算法: 每次用广搜寻找一条最短的增广路（即包含最少的边），然后沿其增广。
费用流 E’K’ 算法: 每次用spfa计算图的距离标号，然后沿着可行边进行增广。

最大流 DINIC 算法: 用广搜获得每个点到源点的距离标号，增广时沿距离标号严格减1的路径增广，直到网络中不再存在这么一条路径，那么重新广搜计算距离标号，如果广搜发现整个源点到汇点已经不连通那么退出算法。
费用流 原始对偶 算法: 用 SPFA 获得每个点到源点的最短路，增广时沿着最短路前进的方向增广, 直到网络中不存在一条路径时重新 SPFA 求最短路, 直到没有一条最短路可以到达汇点为止。

最大流 SAP 算法: 与 dinic 一样基于距离标号，不过这里保存的是到汇点的距离标号。并且考虑每次增广对网络的影响，发现增广只会使点的距离标号变大，并且并不会破坏距离标号 dis[u]<=dis[v]+w[u,v]   的性质，只会使得等号不再成立。找不到可行边就是因为没有一个结点v使得dis[u]==dis[v]+w[u,v]   。那么重新使等号成立的方法也很简单，并不需要重新计算整个图的距离标号，只需要调整距离标号：如果从u点开始寻找增广路没有成功，即没有一个v使得dis[u]==dis[v]+w[u,v]那么在所有（v∈V）中找到距离标号最小的一个v，使dis[u]=dis[v]+w[u,v]  

 即可。

费用流 ZKW 算法: 每次增广，同样不会破坏距离标号dis[u]<=dis[v]+w[u,v] ，只会使得等号不再成立。并且被破坏的点并没有很多（只有在增广路上的点有可能被破坏）。因此并不需要SPFA来重新计算全部的距离标号。如果某一次寻找可行边组成增广路的尝试进行到点u失败，那么在所有的边$（v∈V中找到距离标号最小的一个v，使中找到距离标号最小的一个v，使dis[v] == dis[v] + w[u, v]&成立即可。

算法实现

#include <queue>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int MAXN = 1010;
const int MAXM = 1000100;
const int MAXN_INT = (1 << 29);
 
struct Edge{
    int v, w, c, nxt;
};
 
struct Node{
    int id, v;
};
 
bool vis[MAXN];
Node pre[MAXN];
Edge edge[MAXN];
int n, m, ecnt, sumFlow;
int head[MAXN], dis[MAXN];
 
void init(){
    ecnt = 0;
    memset(edge, 0, sizeof(edge));
    memset(head, -1, sizeof(head));
}
 
void addEdge(int u, int v, int c, int w){
    edge[ecnt].v = v;
    edge[ecnt].w = w;
    edge[ecnt].c = c;
    edge[ecnt].nxt = head[u];
    head[u] = ecnt++;
}
 
bool SPFA(int s, int t, int n){
    queue <int> que;
    memset(vis, 0, sizeof(vis));
    fill(dis, dis + MAXN, MAXN_INT);
    vis[s] = true;
    dis[s] = 0;
    que.push(s);
    while(!que.empty()){
        int u =que.front();
        que.pop();
        vis[u] = false;
        for(int i = head[u]; i + 1; i = edge[i].nxt){
            int v = edge[i].v;
            if(edge[i].c && dis[v] > dis[u] + edge[i].c){
                dis[v] = dis[u] + edge[i].c;
                pre[v].v = u;
                pre[v].id = i;
                if(!vis[v]){
                    que.push(v);
                    vis[v] = true;
                }
            }
        }
    }
    if(dis[t] == MAXN_INT) return false;
    return true;
}
 
int MCMF(int s, int t, int n){
    int flow = 0;
    int minCost = 0;
    while(SPFA(s, t, n)){
        int minFlow = MAXN_INT + 1;
        for(int i = t; i != s; i = pre[i].v){
            minFlow = min(minFlow, edge[pre[i].id].w);
        }
 
        for(int i = t; i != s; i = pre[i].v){
            edge[pre[i].id].w -= minFlow;
            edge[pre[i].id ^ 1].w += minFlow;
        }
        minCost += dis[t] * minFlow;
    }
    sumFlow = flow;
    return minCost;
}
 
int main(){
    while(scanf("%d%d", &n, &m) != EOF){
        int u, v, c, w;
        for(int i = 0; i < m; i++){
            scanf("%d%d%d%d", &u, &v, &c, &w);
            addEdge(u, v, c, w);
            addEdge(v, u, -c, 0);
        }
        int ans = MCMF(1, n, n);
        printf("%d\n", ans);
    }
    return 0;
}

训练指南网络流题集

Diposting di 2019-04-24 | Edited on 2019-02-06

A.UVA - 11248 (最大流，最小割)

UVA - 11248 Frequency Hopping

题意

给定一个有向网络，每条边均有一个容量。问是否存在一个从点1到点N，流量为C的流。如果不存在，是否可以恰好修改一条弧的容量，使得存在这样的流。

思路

先求一遍最大流，如果大于等于C，那么就直接输出possible。

否则的话就是最大流达不到C，那么对哪些边进行扩容呢，肯定是选择最小割！

将最小割的边集全部求出来，之后每条边都尝试将容量变为C，看看能否达到要求。

优化一：求完最大流后把流量留着，以后每次在它的基础上增广。

优化二：每次没必要求出最大流，增广到流量至少为C时就可以停下来。

搞不到为什么刘汝佳代码那么快

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
struct Edge{
    int from,to,cap,flow;
    Edge(int u,int v,int c,int f)
    :from(u),to(v),cap(c),flow(f){}
    bool operator<(const Edge& a)const{
        return from<a.from||(from==a.from&&to<a.to);
    }
};
struct Dinic{
    int n,m,s,t;
    vector<Edge>edges;
    vector<int>G[maxn];
    bool vis[maxn];
    int d[maxn];
    int cur[maxn];
    void init(int n){
        this->n=n;
        for(int i=0;i<n;i++)G[i].clear();
        edges.clear();
    }
    void ClearFlow(){
        for(int i=0;i<edges.size();i++)edges[i].flow=0;
    }
    void AddEdge(int from,int to,int cap){
        edges.push_back(Edge(from,to,cap,0));
        edges.push_back(Edge(to,from,0,0));
        m=edges.size();
        G[from].push_back(m-2);
        G[to].push_back(m-1);
    }
    bool BFS(){
        memset(vis,0,sizeof(vis));
        memset(d,0,sizeof(d));
        queue<int>q;
        q.push(s);
        d[s]=0;
        vis[s]=1;
        while(!q.empty()){
            int x=q.front();
            q.pop();
            for(int i=0;i<G[x].size();i++){
                Edge& e=edges[G[x][i]];
                if(!vis[e.to]&&e.cap>e.flow){
                    vis[e.to]=1;
                    d[e.to]=d[x]+1;
                    q.push(e.to);
                }
            }
        }
        return vis[t];
    }
    int DFS(int x,int a){
        if(x==t||a==0)return a;
        int flow=0,f;
        for(int &i=cur[x];i<G[x].size();i++){
            Edge& e=edges[G[x][i]];
            if(d[x]+1==d[e.to]&&(f=DFS(e.to,min(a,e.cap-e.flow)))>0){
                e.flow+=f;
                edges[G[x][i]^1].flow-=f;
                flow+=f;
                a-=f;
                if(a==0)break;
            }
        }
        return flow;
    }
    int Maxflow(int s,int t){
        this->s=s;this->t=t;
        int flow=0;
        while(BFS()){
            memset(cur,0,sizeof(cur));
            flow+=DFS(s,inf);
        }
        return flow;
    }
    vector<int>Mincut(){ /// call this after maxflow
        vector<int>ans;
        for(int i=0;i<edges.size();i++){
            Edge& e=edges[i];
            if(vis[e.from]&&!vis[e.to]&&e.cap>0)ans.push_back(i);
        }
        return ans;
    }
    void Reduce(){
        for(int i=0;i<edges.size();i++)edges[i].cap-=edges[i].flow;
    }
}g;

int main()
{
    int n,e,c,kase=0;
    while(scanf("%d%d%d",&n,&e,&c)==3&&n){
        g.init(n);
        while(e--){
            int a,b,c;
            scanf("%d%d%d",&a,&b,&c);
            g.AddEdge(a-1,b-1,c);
        }
        int flow=g.Maxflow(0,n-1);
        printf("Case %d: ",++kase);
        if(flow>=c)printf("possible\n");
        else{
            vector<int>cut=g.Mincut();
            g.Reduce();
            vector<Edge>ans;
            for(int i=0;i<cut.size();i++){
                Edge& e=g.edges[cut[i]];
                e.cap=c;
                g.ClearFlow();
                if(flow+g.Maxflow(0,n-1)>=c)ans.push_back(e);
                e.cap=0;
            }
            if(ans.empty())printf("not possible\n");
            else{
                sort(ans.begin(),ans.end());
                printf("possible option:(%d,%d)", ans[0].from+1, ans[0].to+1);
                for(int i = 1; i < ans.size(); i++)
                printf(",(%d,%d)", ans[i].from+1, ans[i].to+1);
                printf("\n");
            }
        }
    }
    return 0;
}

B.UVALive - 2531 （构图最大流）

题意

有 n 个队伍进行比赛，每个队伍比赛数目是一样的，每场恰好一个胜一个负，给定每个队伍当前胜的场数败的数目，以及两个队伍剩下的比赛场数，问你冠军队伍可能是哪些队。

思路

对每个队伍 i 进行判断是不是能冠军，最优的情况的就是剩下的比赛全都胜，也就是一共胜的数目就是剩下的要比赛的数再加上原来胜的数目sum，然后把每两个队伍比赛看成一个结点，(u, v)，然后从 s 向结点加一条容量要打的比赛数目的容量，然后从 (u, v) 向 u 和 v 分别加一条容量为无穷大的边，然后每个 u 向 t 加一条容量为 sum - w[i] ，跑一个最大流，如果是满流是，那么就是有解，也就是 i 可能是冠军。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=700+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
struct Edge{
    int from,to,cap,flow;
    Edge(int u,int v,int c,int f)
    :from(u),to(v),cap(c),flow(f){}
    bool operator<(const Edge& a)const{
        return from<a.from||(from==a.from&&to<a.to);
    }
};
struct Dinic{
    int n,m,s,t;
    vector<Edge>edges;
    vector<int>G[maxn];
    bool vis[maxn];
    int d[maxn];
    int cur[maxn];
    void init(int n){
        this->n=n;
        for(int i=0;i<n;i++)G[i].clear();
        edges.clear();
    }
    void AddEdge(int from,int to,int cap){
        edges.push_back(Edge(from,to,cap,0));
        edges.push_back(Edge(to,from,0,0));
        m=edges.size();
        G[from].push_back(m-2);
        G[to].push_back(m-1);
    }
    bool BFS(){
        memset(vis,0,sizeof(vis));
        memset(d,0,sizeof(d));
        queue<int>q;
        q.push(s);
        d[s]=0;
        vis[s]=1;
        while(!q.empty()){
            int x=q.front();
            q.pop();
            for(int i=0;i<G[x].size();i++){
                Edge& e=edges[G[x][i]];
                if(!vis[e.to]&&e.cap>e.flow){
                    vis[e.to]=1;
                    d[e.to]=d[x]+1;
                    q.push(e.to);
                }
            }
        }
        return vis[t];
    }
    int DFS(int x,int a){
        if(x==t||a==0)return a;
        int flow=0,f;
        for(int &i=cur[x];i<G[x].size();i++){
            Edge& e=edges[G[x][i]];
            if(d[x]+1==d[e.to]&&(f=DFS(e.to,min(a,e.cap-e.flow)))>0){
                e.flow+=f;
                edges[G[x][i]^1].flow-=f;
                flow+=f;
                a-=f;
                if(a==0)break;
            }
        }
        return flow;
    }
    int Maxflow(int s,int t){
        this->s=s;this->t=t;
        int flow=0;
        while(BFS()){
            memset(cur,0,sizeof(cur));
            flow+=DFS(s,inf);
        }
        return flow;
    }
}g;
const int maxt=25+5;
int n,w[maxt],d[maxt],a[maxt][maxt];
inline int ID(int u,int v){return u*n+v+1;}
inline int ID(int u){return n*n+u+1;}
bool canWin(int team){
    int total=w[team];
    for(int i=0;i<n;i++)total+=a[team][i];
    for(int i=0;i<n;i++)
        if(w[i]>total)return false;
    g.init(n*n+n+2);
    int full=0;
    int s=0,t=n*n+n+1;
    for(int u=0;u<n;u++){
        for(int v=u+1;v<n;v++){
            if(a[u][v]>0)g.AddEdge(s,ID(u,v),a[u][v]);
            full+=a[u][v];
            g.AddEdge(ID(u,v),ID(u),inf);
            g.AddEdge(ID(u,v),ID(v),inf);
        }
        if(w[u]<total)g.AddEdge(ID(u),t,total-w[u]);
    }
    return g.Maxflow(s,t)==full;
}
int main()
{
    int t;
    cin>>t;
    while(t--){
        cin>>n;
        for(int i=0;i<n;i++)cin>>w[i]>>d[i];
        for(int i=0;i<n;i++)
            for(int j=0;j<n;j++)cin>>a[i][j];
        bool first=true;
        for(int i=0;i<n;i++)
        if(canWin(i)){
            if(first)first=false;else cout<<" ";
            cout<<i+1;
        }
        cout<<endl;
    }
    return 0;
}

C.UVA - 10779 (构图最大流)

题意

Bob与他的朋友交换贴纸;他的这些朋友只交换自己没有的贴纸;且用的是自己所有的重复贴纸;现在要求Bob最大能得到多少张贴纸; （Bob可以不只用重复的贴纸）

思路

把人和物品都进行编号,添加原点s和汇点e,s到每个物品连边容量为Bob拥有的数目;所有物品向汇点e连边容量为1;

如果一个人向他拥有的物品连边,容量为数目减1,表示他自己会留一个;如果他不拥有某件物品,则物品向这个人连一条边,表示这个人最多接受一件这个物品;

然后跑一遍最大流就是答案了;

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=700+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
struct Edge{
    int from,to,cap,flow;
    Edge(int u,int v,int c,int f)
    :from(u),to(v),cap(c),flow(f){}
    bool operator<(const Edge& a)const{
        return from<a.from||(from==a.from&&to<a.to);
    }
};
struct Dinic{
    int n,m,s,t;
    vector<Edge>edges;
    vector<int>G[maxn];
    bool vis[maxn];
    int d[maxn];
    int cur[maxn];
    void init(int n){
        this->n=n;
        for(int i=0;i<n;i++)G[i].clear();
        edges.clear();
    }
    void AddEdge(int from,int to,int cap){
        edges.push_back(Edge(from,to,cap,0));
        edges.push_back(Edge(to,from,0,0));
        m=edges.size();
        G[from].push_back(m-2);
        G[to].push_back(m-1);
    }
    bool BFS(){
        memset(vis,0,sizeof(vis));
        memset(d,0,sizeof(d));
        queue<int>q;
        q.push(s);
        d[s]=0;
        vis[s]=1;
        while(!q.empty()){
            int x=q.front();
            q.pop();
            for(int i=0;i<G[x].size();i++){
                Edge& e=edges[G[x][i]];
                if(!vis[e.to]&&e.cap>e.flow){
                    vis[e.to]=1;
                    d[e.to]=d[x]+1;
                    q.push(e.to);
                }
            }
        }
        return vis[t];
    }
    int DFS(int x,int a){
        if(x==t||a==0)return a;
        int flow=0,f;
        for(int &i=cur[x];i<G[x].size();i++){
            Edge& e=edges[G[x][i]];
            if(d[x]+1==d[e.to]&&(f=DFS(e.to,min(a,e.cap-e.flow)))>0){
                e.flow+=f;
                edges[G[x][i]^1].flow-=f;
                flow+=f;
                a-=f;
                if(a==0)break;
            }
        }
        return flow;
    }
    int Maxflow(int s,int t){
        this->s=s;this->t=t;
        int flow=0;
        while(BFS()){
            memset(cur,0,sizeof(cur));
            flow+=DFS(s,inf);
        }
        return flow;
    }
}g;
const int maxt=30+5;
int n,w[maxt],d[maxt],a[maxt][maxt],m;
inline int ID(int u){return u;}///物品
inline int PID(int u){return m+u;}
int S,T;
void build(){
    for(int i=1;i<=m;i++){
        if(a[1][i])
            g.AddEdge(S,i,a[1][i]);
    }
    for(int i=2;i<=n;i++){
        for(int j=1;j<=m;j++){
            if(a[i][j]>=2){
                g.AddEdge(PID(i),ID(j),a[i][j]-1);
            }
            else if(!a[i][j]){
                g.AddEdge(ID(j),PID(i),1);
            }
        }
    }
    for(int i=1;i<=m;i++){
        g.AddEdge(ID(i),T,1);
    }
}
int main()
{
    int t;
    int cast=1;
    cin>>t;
    while(t--){
        cin>>n>>m;
        g.init(n+m+2);
        memset(a,0,sizeof(a));
        for(int i=1;i<=n;i++){
            int tot;cin>>tot;
            while(tot--){
                int aa;
                cin>>aa;
                a[i][aa]++;
            }
        }
        S=0,T=n+m+1;
        build();
        cout<<"Case #"<<cast++<<": ";
        cout<<g.Maxflow(S,T)<<endl;
    }
    return 0;
}

D.UVA - 11613 (最大费用流)

题意

A公司生产一种元素，给出该元素在未来M个月中每个月的单位售价，最大生产量，生产成本，最大销售量和最大存储时间，和每月存储代价，问这家公司在M个月内所能赚大的最大利润

思路

建边的时候，费用我用的是相反数，所以得到最小费用后要去相反数
MCMF的时候，用一个数组纪录了到达汇点时所花费的最小价值，因为取的是相反数，所以当价值为正时，就表示已经亏本了，所以可以退出了

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=700+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
struct Edge{
    int from,to,cap,flow,cost;
    Edge(int u,int v,int c,int f,int w)
    :from(u),to(v),cap(c),flow(f),cost(w){}
};
struct MCMF{
    int n,m;
    vector<Edge>edges;
    vector<int>G[maxn];
    int inq[maxn];
    int d[maxn];
    int p[maxn];
    int a[maxn];
    void init(int n){
        this->n=n;
        for(int i=0;i<n;i++)G[i].clear();
        edges.clear();
    }
    void AddEdge(int from,int to,int cap,int cost){
        edges.emplace_back(from,to,cap,0,cost);
        edges.emplace_back(to,from,0,0,-cost);
        m=edges.size();
        G[from].push_back(m-2);
        G[to].push_back(m-1);
    }
    bool BellmanFord(int s,int t,int& flow,ll& cost){
        for(int i=0;i<n;i++)d[i]=inf;
        memset(inq,0,sizeof(inq));
        d[s]=0;
        inq[s]=1;
        p[s]=0;
        a[s]=inf;
        queue<int>q;
        q.push(s);
        while(!q.empty()){
            int u=q.front();
            q.pop();
            inq[u]=0;
            for(int i=0;i<G[u].size();i++){
                Edge& e=edges[G[u][i]];
                if(e.cap>e.flow&&d[e.to]>d[u]+e.cost){
                    d[e.to]=d[u]+e.cost;
                    p[e.to]=G[u][i];
                    a[e.to]=min(a[u],e.cap-e.flow);
                    if(!inq[e.to]){
                        q.push(e.to);
                        inq[e.to]=1;
                    }
                }
            }
        }
        if(d[t]>0)return false;
        flow+=a[t];
        cost+=(ll)d[t]*(ll)a[t];
        for(int u=t;u!=s;u=edges[p[u]].from){
            edges[p[u]].flow+=a[t];
            edges[p[u]^1].flow-=a[t];
        }
        return true;
    }
    int MincostMaxflow(int s,int t,ll& cost){
        int flow=0;
        cost=0;
        while(BellmanFord(s,t,flow,cost));
        return flow;
    }
}g;

int main()
{
    int t;
    int cast=1;
    cin>>t;
    int month,st_cost;
    while(t--){
        cin>>month>>st_cost;
        g.init(month*2+2);
        int source=0,sink=2*month+1;
        for(int i=1;i<=month;i++){
            int make_cost,make_limit,price,sell_limit,max_store;
            cin>>make_cost>>make_limit>>price>>sell_limit>>max_store;
            g.AddEdge(source,i,make_limit,make_cost);
            g.AddEdge(month+i,sink,sell_limit,-price);
            for(int j=0;j<=max_store;j++){
                if(i+j<=month)
                    g.AddEdge(i,month+i+j,inf,st_cost*j);
            }
        }
        ll cost=0;g.MincostMaxflow(source,sink,cost);
        cout<<"Case "<<cast++<<": "<<-cost<<endl;
    }
    return 0;
}

个人模板整理

Diposting di 2019-04-24 | Edited on 2019-10-09

数据结构

字符串处理

KMP

/*
* next[] 的含义：x[i-next[i]...i-1]=x[0...next[i]-1] 
* next[i] 为满足 x[i-z...i-1]=x[0...z-1] 的最大 z 值（就是 x 的自身匹配）
*/ 
void kmp_pre(char x[],int m,int next[]){
    int i,j;
    j=next[0]=-1;
    i=0;
    while(i<m){
        while(-1!=j&&x[i]!=x[j])j=next[j];
        next[++i]=++j;
    }
}
/* 
 * kmpNext[i] 的意思:next'[i]=next[next[...[next[i]]]](直到 next'[i]<0 或者 x[next'[i]]!=x[i])
 * 这样的预处理可以快一些 
 */ 
void preKmp(char x[],int m,int kmpNext[]){
    int i,j;
    j=kmpNext[0]=-1;
    i=0;
    while(i<m){
        while(-1!=j && x[i]!=x[j])j=kmpNext[j];
        if(x[++i]==x[++j])kmpNext[i]=kmpNext[j];
        else kmpNext[i]=j;
    }
}
/*
返回x 在 y 中出现的次数，可以重叠
*/
int mynext[maxn];
int kmp(char x[],int m,char y[],int n){ // x是模式串 ，y是主串
    int i,j;
    int ans=0;
    kmp_pre(x,m,mynext);
    i=j=0;
    while(i<n){
        while(-1!=j&&y[i]!=y[j])j=mynext[j];
        i++;j++;
        if(j>=m){
            ans++;
            j=mynext[j];
        }
    }
    return ans;
}

e-KMP

/*
 * 扩展KMP算法
 */
// next[i]:x[i...m-1] 与x[0...m-1]的最长公共前缀
void pre_EKMP(char x[],int m,int next[]){
    next[0]=m;
    int j=0;
    while(j+1<m && x[j] == x[j+1])j++;
    next[1]=j;
    int k=1;
    for(int i=2;i<m;i++){
        int p=next[k]+k-1;
        int L=next[i-k];
        if(i+L < p+1)next[i]=L;
        else{
            j=max(0,p-i+1);
            while( i+j < m && x[i+j] == x[j])j++;
            next[i]=j;
            k=i;
        }
    }
}
void EKMP(char x[],int m,int y[],int n,int next[],int extend[]){
    pre_EKMP(x,m,next);
    int j=0;
    while(j < n && j < m && x[j] == y[j])j++;
    extend[0]=j;
    int k=0;
    for(int i = 1;i < n;i++){
        int p = extend[k]+k-1;
        int L=next[i-k];
        if(i+L < p+1)extend[i]=L;
        else{
            j=max(0,p-i+1);
            while(i+j < n && j < m && y[i+j] == x[j])j++;
            extend[i]=j;
            k=i;
        }
    }
}

Z-算法

//求每个位置匹配前缀的长度的最大值  s[0…z[i]-1]=s[i…i+z[i]-1]
vector<int> ZF(const string &s){
    vector<int>z(s.size());
    int l=0,r=1;
    for(int i=1;i<(int)s.size();i++){
        if(r>i)z[i]=min(z[i-l],r-i);
        if(z[i]+i>=r){
            l=i,r=z[i]+i;
            while(r<(int)s.size()&&s[r]==s[r-l])r++;
            z[i]=r-l;
        }
    }
    return z;
}

最大最小表达式

int getminmax(bool flag,string s){
    int i=0,j=1,k=0;
    int len=s.length();
    while(i<len&&j<len&&k<len){
        int t=s[(i+k)%len]-s[(j+k)%len];
        if(t==0)k++;
        else{
            if(!flag){
                if(t>0)i=i+k+1;
                else   j=j+k+1;
            }
            else{
                if(t>0)j=j+k+1;
                else   i=i+k+1;
            }
            if(i==j)j++;
            k=0;
        }
    }
    return i<j?i:j;
}

Manacher

char Ma[maxn*2];
int Mp[maxn*2]; ///需要-1才是最长回文的长度
int Manacher(char s[],int len){
    int l=0,ans=0;
    Ma[l++]='$';
    Ma[l++]='#';
    for(int i=0;i<len;i++){
        Ma[l++]=s[i];
        Ma[l++]='#';
    }
    Ma[l]=0;
    int mx=0,id=0;
    for(int i=0;i<l;i++){
        Mp[i]=mx>i?min(Mp[2*id-i],mx-i):1;
        while(Ma[i+Mp[i]]==Ma[i-Mp[i]])Mp[i]++;
        if(i+Mp[i]>mx){
            mx=i+Mp[i];
            id=i;
        }
        ans+=Mp[i]/2;
    }
    return ans;///计算共有多少回文串
}
/* 
 * abaaba
 * i: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 
 * Ma[i]: $ # a # b # a # a # b # a # 
 * Mp[i]: 1 1 2 1 4 1 2 7 2 1 4 1 2 1 
 */

Manacher返回最长回文串

string Manacher(string s) {
    // Insert '#'
    string t = "$#";
    for (int i = 0; i < s.size(); ++i) {
        t += s[i];
        t += "#";
    }
    int mx=0;
    // Process t
    vector<int> p(t.size(), 0);
    int mx = 0, id = 0, resLen = 0, resCenter = 0;
    for (int i = 1; i < t.size(); ++i) {
        p[i] = mx > i ? min(p[2 * id - i], mx - i) : 1;
        while (t[i + p[i]] == t[i - p[i]]) ++p[i];
        if (mx < i + p[i]) {
            mx = i + p[i];
            id = i;
        }
        if (resLen < p[i]) {
            resLen = p[i];
            resCenter = i;
        }
        mx=max(mx,p[i]);
    }
    cout<<mx-1<<endl;
    return s.substr((resCenter - resLen) / 2, resLen - 1);
}

字符串哈希

typedef unsigned long long ull;
const ull Seed_Pool[] = {146527, 19260817};
const ull Mod_Pool[] = {1000000009, 998244353};
struct Hash
{
    ull SEED, MOD;
    vector<ull> p, h;
    Hash() {}
    Hash(const string& s, const int& seed_index, const int& mod_index)
    {
        SEED = Seed_Pool[seed_index];
        MOD = Mod_Pool[mod_index]; 
        int n = s.length();
        p.resize(n + 1), h.resize(n + 1);
        p[0] = 1;
        for (int i = 1; i <= n; i++) p[i] = p[i - 1] * SEED % MOD;
        for (int i = 1; i <= n; i++) h[i] = (h[i - 1] * SEED % MOD + s[i - 1]) % MOD;
    }
    ull get(int l, int r) { return (h[r] - h[l] * p[r - l] % MOD + MOD) % MOD; }
    ull substr(int l, int m) { return get(l, l + m); }
};

    p[0]=1;
    for(int i=1;i<=3e5+10;i++)p[i]=p[i-1]*233;
        for(int i=1;i<=len;i++){
            h[i]=(h[i-1]*233+s[i]);
        }
ull get(int l,int r){
    return h[r]-h[l-1]*p[r-l+1];
}
bool check(int l,int r){
    int len=(r-l+1);
    int mid=(l+r)/2;
    if(len&1)return get(l,mid)==get(mid,r);
    else return get(l,mid)==get(mid+1,r);
}

回文树

const int MAXN = 100005 ;  
const int N = 26 ;  

struct Palindromic_Tree {  
    //cnt最后count一下之后是那个节点代表的回文串出现的次数
    int next[MAXN][N] ;//next指针，next指针和字典树类似，指向的串为当前串两端加上同一个字符构成  
    int fail[MAXN] ;//fail指针，失配后跳转到fail指针指向的节点  
    int cnt[MAXN] ; //表示节点i表示的本质不同的串的个数（建树时求出的不是完全的，最后count()函数跑一遍以后才是正确的） 
    int num[MAXN] ; //表示以节点i表示的最长回文串的最右端点为回文串结尾的回文串个数
    int len[MAXN] ;//len[i]表示节点i表示的回文串的长度（一个节点表示一个回文串）
    int S[MAXN] ;//存放添加的字符  
    int last ;//指向新添加一个字母后所形成的最长回文串表示的节点。
    int n ;//表示添加的字符个数。
    int p ;//表示添加的节点个数。

    int newnode ( int l ) {//新建节点  
        for ( int i = 0 ; i < N ; ++ i ) next[p][i] = 0 ;  
        cnt[p] = 0 ;  
        num[p] = 0 ;  
        len[p] = l ;  
        return p ++ ;  
    }  

    void init () {//初始化  
        p = 0 ;  
        newnode (  0 ) ;  
        newnode ( -1 ) ;  
        last = 0 ;  
        n = 0 ;  
        S[n] = -1 ;//开头放一个字符集中没有的字符，减少特判  
        fail[0] = 1 ;  
    }  

    int get_fail ( int x ) {//和KMP一样，失配后找一个尽量最长的  
        while ( S[n - len[x] - 1] != S[n] ) x = fail[x] ;  
        return x ;  
    }  

    void add ( int c ) {  
        c -= 'a' ;  
        S[++ n] = c ;  
        int cur = get_fail ( last ) ;//通过上一个回文串找这个回文串的匹配位置  
        if ( !next[cur][c] ) {//如果这个回文串没有出现过，说明出现了一个新的本质不同的回文串  
            int now = newnode ( len[cur] + 2 ) ;//新建节点  
            fail[now] = next[get_fail ( fail[cur] )][c] ;//和AC自动机一样建立fail指针，以便失配后跳转  
            next[cur][c] = now ;  
            num[now] = num[fail[now]] + 1 ;  
        }  
        last = next[cur][c] ;  
        cnt[last] ++ ;  
    }  

    void count () {  
        for ( int i = p - 1 ; i >= 0 ; -- i ) cnt[fail[i]] += cnt[i] ;  
        //父亲累加儿子的cnt，因为如果fail[v]=u，则u一定是v的子回文串！  
    }  
} ;

struct PAT{
    struct node{
        int len,num,fail,son[26];
    }t[maxn];
    int last,n,tot,s[maxn],x[maxn],y[maxn];ll sum[maxn];
    void init(int len){
        for(int i=0;i<=len+10;i++){
            t[i].fail=t[i].num=t[i].len=0;
            for(int j=0;j<26;j++)t[i].son[j]=0;
            x[i]=y[i]=0;sum[i]=0;
        }
        tot=last=1;n=0;
        t[0].len=0;t[1].len=-1;
        t[0].fail=t[1].fail=1;
        s[0]=-1;
    }
    void add(int c){
        int p=last;s[++n]=c;
        while(s[n]!=s[n-1-t[p].len])p=t[p].fail;
        if(!t[p].son[c]){
            int v=++tot,k=t[p].fail;
            while(s[n]!=s[n-1-t[k].len])k=t[k].fail;
            t[v].fail=t[k].son[c];
            t[v].len=t[p].len+2;
            t[v].num=t[t[v].fail].num+1;///可以通过深度来求所有回文个数
            t[p].son[c]=v;
        }
        last=t[p].son[c];
        sum[last]++;
    }
    void solve(){
        for(int i=tot;i>=2;i--){
            if(x[i]==0)x[i]=i;
            while(x[i]>=2&&t[x[i]].len>(t[i].len+1)/2)x[i]=t[x[i]].fail;
            if(x[i]>=2&&t[x[i]].len==(t[i].len+1)/2)y[i]=1;
            x[t[i].fail]=x[i];
        }

        for(int i=tot;i>=2;i--){
            sum[t[i].fail]+=sum[i]; 
            if(y[i])ans[t[i].len]+=sum[i];
        }
    }
}T;

支持前后端插入回文树

struct PAT
{
    struct node{
        int len,num,fail,son[26];
    }t[maxn];
    int n,tot,s[maxn<<1],L,R,suf,pre; ll ans;
    void init()
    {
        memset(t,0,sizeof(t));
        memset(s,-1,sizeof(s));
        tot=1; L=100000; R=L-1;
        suf=pre=0; ans=0;
        t[1].len=-1; t[0].fail=t[1].fail=1;
    }
    void add(int c,int n,int &last,int op){
        int p=last; s[n]=c;
        while(s[n]!=s[n-op-op*t[p].len]) p=t[p].fail;
        if(!t[p].son[c]){
            int v=++tot,k=t[p].fail;
            while(s[n]!=s[n-op*t[k].len-op]) k=t[k].fail;
            t[v].fail=t[k].son[c];
            t[v].len=t[p].len+2;
            t[v].num=t[t[v].fail].num+1;
            t[p].son[c]=v;
        }
        last=t[p].son[c]; ans+=t[last].num;
        if(t[last].len==R-L+1) suf=pre=last;
    }
}T;
 T.add(s[0]-'a',--T.L,T.pre,-1);
 T.add(s[0]-'a',++T.R,T.suf,1);

AC自动机

struct Trie{
    int next[maxm][26],fail[maxm],end[maxm];
    int root,L;
    int newnode(){
    for(int i=0;i<26;i++)
        next[L][i]=-1;
    end[L++]=0;
    return L-1;
    }
    void init(){
        L=0;
        root=newnode();
    }
    void insert(char buf[]){
        int len=strlen(buf);
        int now=root;
        for(int i=0;i<len;i++){
            if(next[now][buf[i]-'a']==-1)
                next[now][buf[i]-'a']=newnode();
            now=next[now][buf[i]-'a'];
        }
        end[now]++;
    }
    void build(){
        queue<int>Q;
        fail[root]=root;
        for(int i=0;i<26;i++)
            if(next[root][i]==-1)
                next[root][i]=root;
            else{
                fail[next[root][i]]=root;
                Q.push(next[root][i]);
            }
        while(!Q.empty()){
            int now=Q.front();
            Q.pop();
            for(int i=0;i<26;i++)
                if(next[now][i]==-1)
                    next[now][i]=next[fail[now]][i];
                else{
                    fail[next[now][i]]=next[fail[now]][i];
                    Q.push(next[now][i]);
                }
        }
    }
    int query(char buf[]){
        int len=strlen(buf);
        int now=root;
        int res=0;
        for(int i=0;i<len;i++){
            now=next[now][buf[i]-'a'];
            int temp=now;
            while(temp!=root){
                res+=end[temp];
                end[temp]=0;
                temp=fail[temp];
            }
        }
        return res;
    }
    void debug(){
        for(int i=0;i<L;i++){
            printf("id =%3d,fail = %3d,end = %3d ,chi = [",i,fail[i],end[i]);
            for(int j=0;j<26;j++)
                printf("%2d",next[i][j]);
            printf("]\n");
        }
    }
};

后缀数组

倍增法

struct DA{
//sa[i]就表示排名为i的后缀的起始位置的下标
//映射数组rk[i]就表示起始位置的下标为i的后缀的排名
/*height 数组的定义：h[i]表示rk为i的后缀与rk为i−1的后缀的最长公共前缀，可以用sa数组和rk数组来O(n)求得，这要用到一个性质：h[rk[i]]>=h[rk[i−1]]−1。也就是说如果根据rk从前往后求，每次暴力匹配来增加长度，结果是近似递增的，可以证明时间复杂度的正确性。性质的证明详见论文
*/
    bool cmp(int *r,int a,int b,int l){
        return r[a]==r[b]&&r[a+l]==r[b+l];
    }
    int t1[maxn],t2[maxn],c[maxn];
    int rank[maxn],height[maxn],RMQ[maxn],mm[maxn];
    int best[20][maxn];
    int r[maxn];
    int sa[maxn];
    int str[maxn];
    void da(int n,int m){
        n++;
        int i,j,p,*x=t1,*y=t2;
        for(i=0;i<m;i++)c[i]=0;
        for(i=0;i<n;i++)c[x[i]=str[i]]++;
        for(i=1;i<m;i++)c[i]+=c[i-1];
        for(i=n-1;i>=0;i--)sa[--c[x[i]]]=i;
        for(j=1;j<=n;j<<=1){
            p=0;
            for(i=n-j;i<n;i++)y[p++]=i;
            for(i=0;i<n;i++)if(sa[i]>=j)y[p++]=sa[i]-j;
            for(i=0;i<m;i++)c[i]=0;
            for(i=0;i<n;i++)c[x[y[i]]]++;
            for(i=1;i<m;i++)c[i]+=c[i-1];
            for(i=n-1;i>=0;i--)sa[--c[x[y[i]]]]=y[i];
            swap(x,y);
            p=1;x[sa[0]]=0;
            for(i=1;i<n;i++)
                x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++;
            if(p>=n)break;
            m=p;
        }
        int k=0;
        n--;
        for(i=0;i<=n;i++)rank[sa[i]]=i;
        for(i=0;i<n;i++){
            if(k)k--;
            j=sa[rank[i]-1];
            while(str[i+k]==str[j+k])k++;
            height[rank[i]]=k;
        }
    }
    void initRMQ(int n){
        for(int i=1;i<=n;i++)RMQ[i]=height[i];
        mm[0]=-1;
        for(int i=1;i<=n;i++)
            mm[i]=((i&(i-1))==0)?mm[i-1]+1:mm[i-1];
        for(int i=1;i<=n;i++)best[0][i]=i;
        for(int i=1;i<=mm[n];i++)
        for(int j=1;j+(1<<i)-1<=n;j++){
            int a=best[i-1][j];
            int b=best[i-1][j+(1<<(i-1))];
            if(RMQ[a]<RMQ[b])best[i][j]=a;
            else best[i][j]=b;
        }
    }
    int askRMQ(int a,int b){
        int t;
        t=mm[b-a+1];
        b-=(1<<t)-1;
        a=best[t][a];b=best[t][b];
        return RMQ[a]<RMQ[b]?a:b;
    }
    int lcp(int a,int b){
        a=rank[a];b=rank[b];
        if(a>b)swap(a,b);
        return height[askRMQ(a+1,b)];
    }
    void print(int n){
        cout<<"sa[] ";
        for(int i=0;i<=n;i++)cout<<sa[i]<<" ";cout<<endl;
        cout<<"rank[] ";
        for(int i=0;i<=n;i++)cout<<rank[i]<<" ";cout<<endl;
        cout<<"height[] ";
        for(int i=0;i<=n;i++)cout<<height[i]<<" ";cout<<endl;
    }
}AA,BB;
//n=8;
//* num[] = { 1, 1, 2, 1, 1, 1, 1, 2, $ }; 注意 num 最后一位为 0，其他 大于 0
//*rank[] = 4, 6, 8, 1, 2, 3, 5, 7, 0 ;rank[0 n-1] 为有效值，rank[n] 必定为 0 无效值
// *sa[] =  8, 3, 4, 5, 0, 6, 1, 7, 2 ;sa[1 n] 为有效值，sa[0] 必定为 n 是 无效值 
//*height[]= 0, 0, 3, 2, 3, 1, 2, 0, 1 ;height[2 n] 为有效值

DC3

struct DA{
    #define F(x) ((x)/3+((x)%3==1?0:tb))
    #define G(x) ((x)<tb?(x)*3+1:((x)-tb)*3+2)
    int sa[maxn*20],rank[maxn*20],height[maxn*20],str[maxn*20];
    int wa[maxn*20],wb[maxn*20],wv[maxn*20],wss[maxn*20];
    int c0(int *r,int a,int b){
        return r[a]==r[b]&&r[a+1]==r[b+1]&&r[a+2]==r[b+2];
    }
    int c12(int k,int *r,int a,int b){
        if(k==2)
            return r[a]<r[b]||(r[a]==r[b]&&c12(1,r,a+1,b+1));
        else return r[a]<r[b]||(r[a]==r[b]&&wv[a+1]<wv[b+1]);
    }
    void sort(int *r,int *a,int *b,int n,int m){
        int i;
        for(i=0;i<n;i++)wv[i]=r[a[i]];
        for(i=0;i<m;i++)wss[i]=0;
        for(i=0;i<n;i++)wss[wv[i]]++;
        for(i=1;i<m;i++)wss[i]+=wss[i-1];
        for(i=n-1;i>=0;i--)
            b[--wss[wv[i]]]=a[i];
    }
    void dc3(int *r,int *sa,int n,int m){
        int i,j,*rn=r+n;
        int *san=sa+n,ta=0,tb=(n+1)/3,tbc=0,p;
        r[n]=r[n+1]=0;
        for(i=0;i<n;i++)if(i%3!=0)wa[tbc++]=i;
        sort(r+2,wa,wb,tbc,m);
        sort(r+1,wb,wa,tbc,m);
        sort(r,wa,wb,tbc,m);
        for(p=1,rn[F(wb[0])]=0,i=1;i<tbc;i++)
            rn[F(wb[i])]=c0(r,wb[i-1],wb[i])?p-1:p++;
        if(p<tbc)dc3(rn,san,tbc,p);
        else for(i=0;i<tbc;i++)san[rn[i]]=i;
        for(i=0;i<tbc;i++)if(san[i]<tb)wb[ta++]=san[i]*3;
        if(n%3==1)wb[ta++]=n-1;
        sort(r,wb,wa,ta,m);
        for(i=0;i<tbc;i++)wv[wb[i]=G(san[i])]=i;
        for(i=0,j=0,p=0;i<ta&&j<tbc;p++)
            sa[p]=c12(wb[j]%3,r,wa[i],wb[j])?wa[i++]:wb[j++];
        for(;i<ta;p++)sa[p]=wa[i++];
        for(;j<tbc;p++)sa[p]=wb[j++];
    }
    void da(int n,int m){
        for(int i=n;i<n*3;i++)str[i]=0;
        dc3(str,sa,n+1,m);
        int i,j,k=0;
        for(i=0;i<=n;i++)rank[sa[i]]=i;
        for(i=0;i<n;i++){
            if(k)k--;
            j=sa[rank[i]-1];
            while(str[i+k]==str[j+k])k++;
            height[rank[i]]=k;
        }
    }
    void print(int n){
        cout<<"sa[] ";
        for(int i=0;i<=n;i++)cout<<sa[i]<<" ";cout<<endl;
        cout<<"rank[] ";
        for(int i=0;i<=n;i++)cout<<rank[i]<<" ";cout<<endl;
        cout<<"height[] ";
        for(int i=0;i<=n;i++)cout<<height[i]<<" ";cout<<endl;
    }
}DA;

后缀自动机

struct SAM{
    int fa[maxn],ch[maxn][26],maxlen[maxn],tot,last;
    int sz[maxn],a[maxn],b[maxn];
    void init(){
        tot=last=1;maxlen[1]=fa[1]=0;
        memset(ch[1],0,sizeof(ch[1]));
    }
    void add(int x){
        int np=++tot,p=last;last=np;
        maxlen[np]=maxlen[p]+1;sz[np]=1;
        memset(ch[np],0,sizeof(ch[np]));
        while(p&&!ch[p][x])ch[p][x]=np,p=fa[p];
        if(!p)fa[np]=1;
        else{
            int q=ch[p][x];
            if(maxlen[q]==maxlen[p]+1)fa[np]=q;
            else{
                int nq=++tot;
                memcpy(ch[nq],ch[q],sizeof(ch[q]));
                fa[nq]=fa[q],fa[np]=fa[q]=nq;
                maxlen[nq]=maxlen[p]+1;
                while(p&&ch[p][x]==q)ch[p][x]=nq,p=fa[p];
            }
        }
    }
    void sort(){///拓扑排序 得到每个集合里的串出现次数
        for(int i=1;i<=tot;i++)a[i]=0;
        for(int i=1;i<=tot;i++)a[maxlen[i]]++;
        for(int i=1;i<=tot;i++)a[i]+=a[i-1];
        for(int i=1;i<=tot;i++)b[a[maxlen[i]]--]=i;
        for(int i=tot;i;i--)sz[fa[b[i]]]+=sz[b[i]];
    }
    int At[maxn],Len[maxn];
    void go(char s[]){
        int len=strlen(s);
        int now=1,nowl=0;
        for(int i=0;i<len;i++){
            int c=s[i]-'a';
            if(ch[now][c])now=ch[now][c],nowl++;
            else{
                while(now&&!ch[now][c])now=fa[now];
                if(!now)now=1,nowl=0;
                else nowl=maxlen[now]+1,now=ch[now][c];
            }
            At[i+1]=now;Len[i+1]=nowl;
        }
    }
}S;

树链剖分

int n,q,a[maxn];
vector<int>G[maxn];
int size[maxn],son[maxn],fa[maxn],dep[maxn],top[maxn];
int id[maxn],pre[maxn],cnt=0;
void dfs1(int u,int f,int deep){
    size[u]=1;
    fa[u]=f;son[u]=0;dep[u]=deep;
    for(int i=0;i<G[u].size();i++){
        int v=G[u][i];
        if(v==f)continue;
        dfs1(v,u,deep+1);
        size[u]+=size[v];
        if(size[v]>size[son[u]])son[u]=v;
    }
}
void dfs2(int u,int root){
    id[u]=++cnt;top[u]=root;pre[cnt]=u;
    if(son[u])dfs2(son[u],root);
    for(int i=0;i<G[u].size();i++){
        int v=G[u][i];
        if(v==fa[u]||v==son[u])continue;
        dfs2(v,v);
    }
}
int sumv[maxn<<2],maxv[maxn<<2];
inline void pushup(int o){
    sumv[o]=sumv[o<<1]+sumv[o<<1|1];
    maxv[o]=max(maxv[o<<1],maxv[o<<1|1]);
}
void build(int o,int l,int r){
    int mid=(l+r)/2;
    if(l==r){
        sumv[o]=maxv[o]=a[pre[l]];return;
    }
    build(o<<1,l,mid);build(o<<1|1,mid+1,r);
    pushup(o);
}
void update(int o,int l,int r,int q,int v){
    int mid=(l+r)/2;
    if(l==r){
        sumv[o]=maxv[o]=v;return;
    }
    if(q<=mid)update(o<<1,l,mid,q,v);
    else update(o<<1|1,mid+1,r,q,v);
    pushup(o);
}
int querysum(int o,int l,int r,int ql,int qr){
    int mid=(l+r)/2,ans=0;
    if(ql<=l&&r<=qr)return sumv[o];
    if(ql<=mid)ans+=querysum(o<<1,l,mid,ql,qr);
    if(qr>mid)ans+=querysum(o<<1|1,mid+1,r,ql,qr);
    return ans;
}
int querymax(int o,int l,int r,int ql,int qr){
    int mid=(l+r)/2,ans=-inf;
    if(ql<=l&&r<=qr)return maxv[o];
    if(ql<=mid)ans=max(ans,querymax(o<<1,l,mid,ql,qr));
    if(qr>mid)ans=max(ans,querymax(o<<1|1,mid+1,r,ql,qr));
    return ans;
}
int qsum(int u,int v){
    int ans=0;
    while(top[u]!=top[v]){
        if(dep[top[u]]<dep[top[v]])swap(u,v);
        ans+=querysum(1,1,n,id[top[u]],id[u]);
        u=fa[top[u]];
    }
    if(dep[u]<dep[v])swap(u,v);
    ans+=querysum(1,1,n,id[v],id[u]);
    return ans;
}
int qmax(int u,int v){
    int ans=-inf;
    while(top[u]!=top[v]){
        if(dep[top[u]]<dep[top[v]])swap(u,v);
        ans=max(ans,querymax(1,1,n,id[top[u]],id[u]));
        u=fa[top[u]];
    }
    if(dep[u]<dep[v])swap(u,v);
    ans=max(ans,querymax(1,1,n,id[v],id[u]));
    return ans;
}

虚树

考虑得到了询问点，如何构造出一棵虚树。
首先我们要先对整棵树dfs一遍，求出他们的dfs序，然后对每个节点以dfs序为关键字从小到大排序
同时维护一个栈，表示从根到栈顶元素这条链
假设当前要加入的节点为p，栈顶元素为x=s[top]，lca为他们的最近公共祖先
因为我们是按照dfs序遍历，因此lca不可能是p
那么现在会有两种情况

1.lca是x，直接将p入栈。
2.x,p分别位于lca的两棵子树中，此时x这棵子树已经遍历完毕，（如果没有，即x的子树中还有一个未加入的点y，但是dfn[y]<dfn[p]，即应先访问y）， 我们需要对其进行构建

设栈顶元素为x，第二个元素为y
若dfn[y]>dfn[lca]，可以连边y−>x，将x出栈；
若dfn[y]=dfn[lca]，即y=lca，连边lca−>x，此时子树构建完毕(break)；
若dfn[y]<dfn[lca]，即lca在y,x之间，连边lca−>x，x出栈，再将lca入栈。此时子树构建完毕(break)。

vector<int>G[maxn];
int dep[maxn],id[maxn],cnt,cnt2;
int a[maxn],vis[maxn];
int fa[maxn][22];
int op[maxn],u[maxn],v[maxn],k[maxn];

void dfs(int u,int f){
    dep[u]=dep[f]+1;
    fa[u][0]=f;
    id[u]=++cnt;
    if(vis[u])a[++cnt2]=u;
    for(auto v:G[u]){
        if(v==f)continue;
        dfs(v,u);
    }
}
void init(){
    for(int i=1;i<=20;i++){
        for(int j=1;j<=n;j++){
            int v=fa[j][i-1];
            fa[j][i]=fa[v][i-1];
        }
    }
}
int lca(int p,int q){
    if(dep[p]<dep[q])swap(p,q);
    for(int i=20;i>=0;i--){
        if(dep[fa[p][i]]>=dep[q])p=fa[p][i];
    }
    if(p==q)return q;
    for(int i=20;i>=0;i--){
        if(fa[p][i]!=fa[q][i])p=fa[p][i],q=fa[q][i];
    }
    return fa[p][0];
}
int S[maxn],top;
int f[maxn];
int sz[maxn];
ll va[maxn],val[maxn]; 
void add(int u,int v){
    if(dep[u]<dep[v])swap(u,v);
    f[u]=v;
    val[u]=0;
    sz[u]=dep[u]-dep[v]-1,va[u]=0; ///链上的个数 和值。
}

void insert(int x){
    if(top==1){
        S[++top]=x;
        return;
    }
    int lc=lca(x,S[top]);
    if(lc==S[top]){
        S[++top]=x;return;
    }
    while(top>1&&id[S[top-1]]>=id[lc])
        add(S[top-1],S[top]),top--;
    if(lc!=S[top])add(lc,S[top]),S[top]=lc;
    S[++top]=x;
}

void build(){
    S[top=1]=0;
    for(int i=1;i<=cnt2;i++)
        insert(a[i]);
    while(top>1)
        add(S[top-1],S[top]),top--;
}
//main
        for(int i=1;i<n;i++){
            int u,v;cin>>u>>v;
            G[u].push_back(v);
            G[v].push_back(u);
        }
        for(int i=1;i<=m;i++){
            cin>>op[i]>>u[i]>>v[i];
            if(op[i]<=3||op[i]==7)cin>>k[i];
            vis[u[i]]=1;vis[v[i]]=1;
        }
        vis[1]=1;
        dfs(1,0);init();
        build();
        for(int i=1;i<=m;i++){
            get(op[i],u[i],v[i],k[i]);
        }

树分治

点分治

int Laxt[maxn<<1],Next[maxn<<1],To[maxn<<1],Len[maxn<<1],ppp;

void add(int u,int v,int w){
    Next[++ppp]=Laxt[u];Laxt[u]=ppp;To[ppp]=v;Len[ppp]=w;
    Next[++ppp]=Laxt[v];Laxt[v]=ppp;To[ppp]=u;Len[ppp]=w;
}
int sz[maxn],d[maxn],vis[maxn],root,sum;
void findroot(int u,int fa){//找重心
    sz[u]=1;d[u]=0;
    for(int i=Laxt[u];i;i=Next[i]){
        int v=To[i];
        if(vis[v]||v==fa)continue;
        findroot(v,u);
        sz[u]+=sz[v];
        d[u]=max(d[u],sz[v]);
    }
    d[u]=max(d[u],sum-sz[u]);
    if(d[u]<d[root])root=u;
}
int dep[maxn],a[maxn];
void dfsdeep(int u,int fa){//计算长度
    a[++a[0]]=dep[u];
    for(int i=Laxt[u];i;i=Next[i]){
        int v=To[i];
        if(vis[v]||v==fa)continue;
        dep[v]=dep[u]+Len[i];
        dfsdeep(v,u);
    }
}
int L;
int cal(int u,int now){//计算答案
    dep[u]=now;a[0]=0;
    dfsdeep(u,0);
    sort(a+1,a+1+a[0]);
    int l=1,r=a[0],ans=0;
    while(l<r){
        if(a[l]+a[r]<=L)ans+=r-l,l++;
        else r--;
    }
    return ans;
}
int ans;
void solve(int u){//解决者
    vis[u]=1;
    ans+=cal(u,0);
    for(int i=Laxt[u];i;i=Next[i]){
        int v=To[i];
        if(vis[v])continue;
        ans-=cal(v,Len[i]);
        sum=sz[v];
        root=0;findroot(v,0);
        solve(root);
    }
}

不需要容斥的点分治

int a[N], dis[10000003];
int md[N], MK, cnt;
void getdis(int now, int pre, int di) {
    if (di > MK)return ;
    md[++cnt] = di;
    for (auto k : v[now]) {
        if (vis[k.fi] || k.fi == pre)continue;
        getdis(k.fi, now, di + k.se);
    }
}
int qa[N], tmp;
void get(int now, int pre) {
    dis[0] = 1;
    for (auto k : v[now]) {
        if (k.fi == pre || vis[k.fi])continue;
        cnt = 0;
        getdis(k.fi, now, k.se);
        for (int i = 1; i <= cnt; ++i) {
            for (int j = 1; j <= m; j++) {
                if (q[j] >= md[i])a[j] |= dis[q[j] - md[i]];
            }
        }
        for (int i = 1; i <= cnt; i++)dis[md[i]] = 1, qa[++tmp] = md[i];
    }
}
void dfs(int now) {
    vis[now] = 1;
    tmp = 0;
    get(now, 0);
    for (int i = 1; i <= tmp; i++)dis[qa[i]] = 0;
    for (auto k : v[now]) {
        if (vis[k.fi])continue;
        rt = 0;
        n = sz[k.fi];
        root(k.fi, 0);
        dfs(rt);
    }
    return ;
}
————————————————
版权声明：本文为CSDN博主「pubgoso」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_40655981/article/details/100886381

动态点分治

/*
给你一颗有点权边权均为1的树
每次操作要么修改某点点权，
要么查询距离u点不超过d距离的所有点权的和
*/
#include<bits/stdc++.h>
using namespace std;
const int maxn=3e5+50;
typedef long long ll;
const int inf=1e9;
int d[maxn*2][20],dep[maxn],id[maxn],w[maxn],cnt;
vector<int>G[maxn];
#define bug cout<<"bug"<<endl;
struct bit{
    int n;
    vector<int>c;
    #define lowbit(x) ((x&-x))
    void init(int m){
        this->n=m;
        c.clear();
        for(int i=0;i<=n;i++)
            c.push_back(0);
    }
    void up(int x,int v){
        if(!x)c[x]+=v;
        for(;x<=n&&x;x+=lowbit(x))
            c[x]+=v;
    }
    int qu(int x){
        if(x>n)x=n;
        int res=c[0];
        for(;x;x-=lowbit(x))
            res+=c[x];
        return res;
    }
    #undef lowbit
}T[maxn*2];
int n,sum,rt,f[maxn],vis[maxn],luo,sz[maxn];
void init(){
    for(int i=1;i<=n;i++)
        G[i].clear(),vis[i]=f[i]=0;
    cnt=0;
}
void dfs(int u,int fa){
    dep[u]=dep[fa]+1;
    d[++cnt][0] = dep[u];
    id[u] = cnt;
    for(auto v:G[u]){
        if(v==fa)continue;
        dfs(v, u);
        d[++cnt][0]=dep[u];
    }
}
void rmq_init(){
    for(int i=1;i<=18;i++)
        for(int j=1;j+(1<<i)-1<=cnt;j++)
            d[j][i]=min(d[j][i-1],d[j+(1<<i-1)][i-1]);
}
int LCA(int x,int y){
    int l=id[x],r=id[y];
    if(l>r)swap(l,r);
    int k=log2(r-l+1);
    return min(d[l][k],d[r+1-(1<<k)][k]);
}
int dis(int x,int y){
    return dep[x]+dep[y]-2*LCA(x,y);
}
void findrt(int u,int fa){
    sz[u]=1;
    int mx=0;
    for(auto v:G[u]){
        if(v==fa||vis[v])continue;
        findrt(v,u);
        sz[u]+=sz[v];
        mx=max(mx,sz[v]);
    }
    mx=max(mx,sum-sz[u]);
    if(mx<luo)luo=mx,rt=u;
}
void divide(int u,int fa){
    f[u]=fa;
    vis[u]=1;
    T[u].init(sum);
    T[u+n].init(sum);
    int tmp=sum;
    for(auto v:G[u]){
        if(v==fa||vis[v])continue;
        sum=(sz[v]>sz[u])?tmp-sz[u]:sz[v];
        luo=inf;
        findrt(v,0);
        divide(rt,u);
    }
}
void up(int u,int v,int val){
    if(!u)return;
    int dist=dis(u,v);
    T[u].up(dist,val);
    if(f[u]){
        int dist2=dis(f[u],v);
        T[u+n].up(dist2,val);
    }
    up(f[u],v,val);
}
int gao(int u,int v,int d){
    int luo=0,dist=dis(u,v);
    if(dist<=d)
        luo+=T[u].qu(d-dist);
    if(f[u]){
        dist=dis(f[u],v);
        if(dist<=d)
            luo-=T[u+n].qu(d-dist);
        luo+=gao(f[u],v,d);
    }
    return luo;
}
int main(){
    int q,u,v;
    char ch;
    while(cin>>n>>q){
        init();
        for(int i=1;i<=n;i++)cin>>w[i];
        for(int i=1;i<n;i++){
            cin>>u>>v;
            G[u].push_back(v);G[v].push_back(u);
        }
        dfs(1,0);
        rmq_init();
        sum=n;
        luo=inf;
        findrt(1,0);
        divide(rt,0);
        for(int i=1;i<=n;i++)up(i,i,w[i]);
        while(q--){
            cin>>ch>>u>>v;
            if(ch=='?')cout<<gao(u,u,v)<<endl;
            else{
                up(u,u,v-w[u]);
                w[u]=v;
            }
        }
    }
    return 0;
}

可以任意删除元素的优先队列


struct node//手搓一个可以删除任意元素的优先队列。
{
    priority_queue<int>q,del;
    void Push(int x){q.push(x);}
    void Erase(int x){del.push(x);}
    int Top()
    {
        while(del.size()&&del.top()==q.top()) del.pop(),q.pop();
        return q.top();
    }
    void Pop()
    {
        while(del.size()&&del.top()==q.top()) del.pop(),q.pop();
        q.pop();
    }
    int Sectop() ///第二大
    {
        int tmp1=Top();Pop();int tmp2=Top();
        Push(tmp1); return tmp2;
    }
    int Size() {return q.size()-del.size();}
}c[maxn],d[maxn],ans;

可持续化字典树

int sum[maxn * 35], son[maxn * 35][2],root[maxn];

void insert(int pos,int pre,int &now,int v){

	now = ++num;
	son[now][0] = son[pre][0];
	son[now][1] = son[pre][1];
	sum[now] = sum[pre] + 1;
	if(pos==-1)
		return;
	bool k = v & (1 << pos);
	insert(pos - 1, son[pre][k], son[now][k], v);
}
int query(int pos,int st,int en,int v){
	//cout << "pos=" << pos << " v=" << v << endl;
	if(pos<0)
		return 0;
	int k = !(v & (1 << pos));
	int tmp = sum[son[en][k]] - sum[son[st][k]];

	if(tmp>0)
		return query(pos - 1, son[st][k], son[en][k], v) + (1 << pos);
	else
		return query(pos - 1, son[st][k ^ 1], son[en][k ^ 1], v);
}
int cnt;

int val[maxn],in[maxn],out[maxn],id[maxn];

void dfs(int u){
	in[u]=++cnt;
	id[cnt]=u;
	insert(30, root[in[u] - 1], root[cnt], val[u]);
	for (int i = Laxt[u]; i;i=Next[i]){
		dfs(To[i]);
	}
	out[u] = cnt;
}

线段树合并

int ls[maxn*40],rs[maxn*40],rt[maxn*40],num[maxn*40],p;
void push_up(int o){
    if(num[ls[o]]>num[rs[o]])num[o]=num[ls[o]],sum[o]=sum[ls[o]];
    else if(num[rs[o]]>num[ls[o]])num[o]=num[rs[o]],sum[o]=sum[rs[o]];
    else num[o]=num[ls[o]],sum[o]=sum[ls[o]]+sum[rs[o]];
}
void update(int &o,int l,int r,int pos){
    if(!o)o=++p;
    if(l==r){
        sum[o]=l;
        num[o]++;
        return;
    }
    int mid=(l+r)/2;
    if(pos<=mid)update(ls[o],l,mid,pos);
    else update(rs[o],mid+1,r,pos);
    push_up(o);
}

int ins(int o,int pre,int l,int r){
    if(!o)return pre;
    if(!pre)return o;
    if(l==r){
        num[o]+=num[pre];
        sum[o]=l;
        return o;
    }
    int mid=(l+r)/2;
    ls[o]=ins(ls[o],ls[pre],l,mid);
    rs[o]=ins(rs[o],rs[pre],mid+1,r);
    push_up(o);
    return o;
}

void dfs(int u,int pre){
    for(int i=Laxt[u];i;i=Next[i]){
        int v=To[i];if(v==pre)continue;
        dfs(v,u);
        rt[u]=ins(rt[u],rt[v],1,1e5);
    }
    update(rt[u],1,1e5,a[u]);
    ans[u]=sum[rt[u]];
}

主席树

int sum[maxn*40],rt[maxn*40];
int lss[maxn*40],rss[maxn*40];
int cnt;
void update(int &o,int pre,int l,int r,int val){
    o=++cnt;
    lss[o]=lss[pre];rss[o]=rss[pre];
    sum[o]=sum[pre];
    if(l==r){sum[o]++;return;}
    int mid=(l+r)/2;
    if(val<=mid)update(lss[o],lss[pre],l,mid,val);
    else update(rss[o],rss[pre],mid+1,r,val);
}
int query(int o,int l,int r,int val){
    if(l==r){
        return sum[o];
    }
    int mid=(l+r)/2;
    if(val<=mid)return query(lss[o],l,mid,val);
    else return query(rss[o],mid+1,r,val);
}
 update(rt[i],rt[i-1],1,1e9,a[i]);
query(rt[r],1,1e9,gc)
    //查询区间这个数的个数

权值线段树

ll sum[maxn*40],val[maxn*40];
int ls[maxn*40],rs[maxn*40];
int cnt;
void update(int &o,int l,int r,int k,int num){
    if(!o)o=++cnt;
    sum[o]+=k;
    val[o]+=1LL*k*num;
    val[o]%=mod;
    if(l==r)return;
    int mid=(l+r)/2;
    if(num<=mid)update(ls[o],l,mid,k,num);
    else update(rs[o],mid+1,r,k,num);
}
ll query(int o,int l,int r,ll k){
    if(l==r)return 1LL*k*l%mod;
    int mid=(l+r)/2;
    ll res=0;
    if(k>sum[ls[o]])res=(val[ls[o]]+query(rs[o],mid+1,r,k-sum[ls[o]]));
    else res=query(ls[o],l,mid,k);
    return res%mod;
}

主席树套树状数组

///动态第K大
int sum[maxn*40],ls[maxn*40],rs[maxn*40],rt[maxn*40];
int op[maxn],ql[maxn],qr[maxn];int cnt;int a[maxn];
int lowbit(int x){return x&(-x);}
void update(int &o,int l,int r,int k,int value){
    if(!o)o=++cnt;sum[o]+=value;
    if(l==r)return;int mid=(l+r)/2;
    if(k<=mid)update(ls[o],l,mid,k,value);
    else update(rs[o],mid+1,r,k,value);
}
int c1,c2;
int q1[maxn],q2[maxn];
int query(int l,int r,int k){
    if(l==r)return l;
    int mid=(l+r)/2;int res=0;
    for(int i=1;i<=c2;i++)res+=sum[ls[q2[i]]];
    for(int i=1;i<=c1;i++)res-=sum[ls[q1[i]]];
    if(k<=res){
        for(int i=1;i<=c2;i++)q2[i]=ls[q2[i]];
        for(int i=1;i<=c1;i++)q1[i]=ls[q1[i]];
        return query(l,mid,k);
    }
    else{
        for(int i=1;i<=c2;i++)q2[i]=rs[q2[i]];
        for(int i=1;i<=c1;i++)q1[i]=rs[q1[i]];
        return query(mid+1,r,k-res);
    }
}
int main(){
    std::ios::sync_with_stdio(false);
    int n,m; cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>a[i];
        for(int j=i;j<=n;j+=lowbit(j))update(rt[j],0,1e9,a[i],1);
    }
    while(m--){
        char ch;
        cin>>ch;
        if(ch=='C'){
            int i,t;cin>>i>>t;
            for(int j=i;j<=n;j+=lowbit(j))update(rt[j],0,1e9,a[i],-1);
            a[i]=t;
            for(int j=i;j<=n;j+=lowbit(j))update(rt[j],0,1e9,a[i],1);
        }
        else{
            int l,r,k;
            cin>>l>>r>>k;c1=c2=0;
            for(int i=l-1;i;i-=lowbit(i))q1[++c1]=rt[i];
            for(int i=r;i;i-=lowbit(i))q2[++c2]=rt[i];
            cout<<query(0,1e9,k)<<endl;
        }
    }
    return 0;
}

树状数组套主席树（二维数点）

int n,m;
int sum[maxn*170],ls[maxn*170],rs[maxn*170],rt[maxn];
int cnt;
int lowbit(int x){return x&(-x);}
int sta[maxn],top;
int newnode(){ ///回收空间
    int p=top?sta[--top]:++cnt;
    ls[p]=rs[p]=sum[p]=0;
    return p;
}
void update(int &o,int l,int r,int k,int v){
    if(!o)o=newnode();
    sum[o]+=v;
    if(l==r)return ;int mid=(l+r)/2;
    if(k<=mid)update(ls[o],l,mid,k,v);
    else update(rs[o],mid+1,r,k,v);
    if(!sum[o])sta[top++]=o,o=0;
}
int query(int o,int l,int r,int ql,int qr){
    if(ql<=l&&qr>=r)return sum[o];
    int mid=(l+r)/2;
    int ans=0;
    if(ql<=mid)ans+=query(ls[o],l,mid,ql,qr);
    if(qr>mid)ans+=query(rs[o],mid+1,r,ql,qr);
    return ans;
}
int pa[maxn],pb[maxn],a[maxn],b[maxn];
int main(){
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);std::cout.tie(0);
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>a[i],pa[a[i]]=i;
    for(int i=1;i<=n;i++)cin>>b[i],pb[b[i]]=i;
    for(int i=1;i<=n;i++){
        for(int j=pa[i];j<=n;j+=lowbit(j))
            update(rt[j],1,n,pb[i],1);
    }
    while(m--){
        int op;cin>>op;
        if(op==1){
            int la,ra,lb,rb;cin>>la>>ra>>lb>>rb;
            int ans=0;
            for(int i=ra;i;i-=lowbit(i)){
                ans+=query(rt[i],1,n,lb,rb);
            }
            for(int i=la-1;i;i-=lowbit(i)){
                ans-=query(rt[i],1,n,lb,rb);
            }
            cout<<ans<<endl;
        }
        else{
            int x,y;
            cin>>x>>y;
            int aa=b[x];
            int bb=b[y];
            for(int i=pa[aa];i<=n;i+=lowbit(i)){
                update(rt[i],1,n,pb[aa],-1);
            }
            for(int i=pa[bb];i<=n;i+=lowbit(i)){
                update(rt[i],1,n,pb[bb],-1);
            }
            swap(b[x],b[y]);pb[b[x]]=x;pb[b[y]]=y;
            for(int i=pa[aa];i<=n;i+=lowbit(i)){
                update(rt[i],1,n,pb[aa],1);
            }
            for(int i=pa[bb];i<=n;i+=lowbit(i)){
                update(rt[i],1,n,pb[bb],1);
            }
        }
    }
    return 0;
}

可持久化并查集

#include<bits/stdc++.h>
using namespace std;
const int maxn=2e5+50;
int n,m;
int fa[maxn*40],cnt;
int rt[maxn*40],ls[maxn*40],rs[maxn*40];
int dep[maxn*40];
void build(int &o,int l,int r){
    o=++cnt;
    if(l==r){fa[o]=l;return;}
    int mid=(l+r)/2;
    build(ls[o],l,mid);build(rs[o],mid+1,r);
}
void merge(int &o,int pre,int l,int r,int pos,int Fa){
    o=++cnt;ls[o]=ls[pre];rs[o]=rs[pre];
    if(l==r){
        fa[o]=Fa;
        dep[o]=dep[pre];
        return;
    }
    int mid=(l+r)/2;
    if(pos<=mid)merge(ls[o],ls[pre],l,mid,pos,Fa);
    else merge(rs[o],rs[pre],mid+1,r,pos,Fa);
}
void update(int o,int l,int r,int pos){
    if(l==r){dep[o]++;return;}
    int mid=(l+r)/2;
    if(pos<=mid)update(ls[o],l,mid,pos);
    else update(rs[o],mid+1,r,pos);
}
int query(int o,int l,int r,int pos){
    if(l==r)return o;
    int mid=(l+r)/2;
    if(pos<=mid)return query(ls[o],l,mid,pos);
    else return query(rs[o],mid+1,r,pos);
}
int find(int o,int pos){
    int now=query(o,1,n,pos);
    if(fa[now]==pos)return now;
    else return find(o,fa[now]);
}
int main(){
    cin>>n>>m;
    build(rt[0],1,n);
    int ans=0;
    for(int i=1;i<=m;i++){
        int op,x,y;
        cin>>op>>x;
        if(op==1){
            cin>>y;
            rt[i]=rt[i-1];
            int posx=find(rt[i],x),posy=find(rt[i],y);
            if(posx!=posy){
                if(dep[posx]>dep[posy])swap(posx,posy);
                merge(rt[i],rt[i-1],1,n,fa[posx],fa[posy]);
                if(dep[posx]==dep[posy])update(rt[i],1,n,fa[posy]);
            }
        }
        else if(op==2)rt[i]=rt[x];
        else{
            cin>>y;
            rt[i]=rt[i-1];
            int posx=find(rt[i],x),posy=find(rt[i],y);
            if(fa[posx]==fa[posy])cout<<1<<endl;
            else cout<<0<<endl;
        }
    }
    return 0;
}

笛卡尔树

        int n,rt;
        cin>>n;
        for(int i=1;i<=n;i++){
            cin>>a[i];
            l[i]=r[i]=0;
            while(!s.empty()&&a[i]>a[s.top()])
                l[i]=s.top(),s.pop();
            if(!s.empty())
                r[s.top()]=i;
            s.push(i);
        }
        while(!s.empty())
            rt=s.top(),s.pop();

void dfs(int u){
    sz[u]=1;
    if(l[u])
        dfs(l[u]),sz[u]+=sz[l[u]];
    if(r[u])
        dfs(r[u]),sz[u]+=sz[r[u]];
    ans=ans*inv[sz[u]]%mod;

二维树状数组

struct BIT2D{
    int n,b[550][550];
    void init(int _n){n=_n;memset(b,0,sizeof(b));}
    void add(int x,int y,int v){
        for(int i=x;i<=n;i+=i&-i)
            for(int j=y;j<=n;j+=j&-j)
                b[i][j]+=v;
    }
    int sum(int x,int y){
        int res=0;
        for(int i=x;i;i-=i&-i)
            for(int j=y;j;j-=j&-j)
                res+=b[i][j];
        return res;
    }
    int sum(int x1,int y1,int x2,int y2){
        return sum(x2,y2)-sum(x1-1,y2)
            -sum(x2,y1-1)+sum(x1-1,y1-1);
    }
}bit;
///区间修改 单点查询
void range_add(int xa, int ya, int xb, int yb, int z){
    add(xa, ya, z);
    add(xa, yb + 1, -z);
    add(xb + 1, ya, -z);
    add(xb + 1, yb + 1, z);
}
///区间修改 区间查询
ll t1[N][N], t2[N][N], t3[N][N], t4[N][N];
void add(ll x, ll y, ll z){
    for(int X = x; X <= n; X += X & -X)
        for(int Y = y; Y <= m; Y += Y & -Y){
            t1[X][Y] += z;
            t2[X][Y] += z * x;
            t3[X][Y] += z * y;
            t4[X][Y] += z * x * y;
        }
}
void range_add(ll xa, ll ya, ll xb, ll yb, ll z){ //(xa, ya) 到 (xb, yb) 的矩形
    add(xa, ya, z);
    add(xa, yb + 1, -z);
    add(xb + 1, ya, -z);
    add(xb + 1, yb + 1, z);
}
ll ask(ll x, ll y){
    ll res = 0;
    for(int i = x; i; i -= i & -i)
        for(int j = y; j; j -= j & -j)
            res += (x + 1) * (y + 1) * t1[i][j]
                - (y + 1) * t2[i][j]
                - (x + 1) * t3[i][j]
                + t4[i][j];
    return res;
}
ll range_ask(ll xa, ll ya, ll xb, ll yb){
    return ask(xb, yb) - ask(xb, ya - 1) - ask(xa - 1, yb) + ask(xa - 1, ya - 1);
}

///一维
/// 单点修改 区间查询
void add(int p, int x){ //这个函数用来在树状数组中直接修改
    while(p <= n) sum[p] += x, p += p & -p;
}
void range_add(int l, int r, int x){ //给区间[l, r]加上x
    add(l, x), add(r + 1, -x);
}
int ask(int p){ //单点查询
    int res = 0; while(p) res += sum[p], p -= p & -p; return res;
}
///区间修改 区间查询
void add(ll p, ll x){
    for(int i = p; i <= n; i += i & -i)
        sum1[i] += x, sum2[i] += x * p;
}
void range_add(ll l, ll r, ll x){
    add(l, x), add(r + 1, -x);
}
ll ask(ll p){
    ll res = 0;
    for(int i = p; i; i -= i & -i)
        res += (p + 1) * sum1[i] - sum2[i];
    return res;
}
ll range_ask(ll l, ll r){
    return ask(r) - ask(l - 1);
}

图论

前向星

int Next[maxn<<1],To[maxn<<1],Laxt[maxn<<1];
int cnt;
void add(int u,int v){
    Next[++cnt]=Laxt[u];Laxt[u]=cnt;To[cnt]=v;
}

深度优先遍历相关

无向图的双连通分量/点双

struct Edge{
    int u,v;
};
///割顶 bccno 无意义
int pre[maxn],iscut[maxn],bccno[maxn],dfs_clock,bcc_cut;
vector<int>G[maxn],bcc[maxn];
stack<Edge>S;
void init(int n){
    for (int i = 0; i < n; i++) G[i].clear();
}
inline void add_edge(int u, int v) { G[u].push_back(v), G[v].push_back(u); }
int dfs(int u,int fa){
    int lowu = pre[u] = ++dfs_clock;
    int child = 0;
    for(int i = 0; i < G[u].size(); i++){
        int v =G[u][i];
        Edge e = (Edge){u,v};
        if(!pre[v]){ ///没有访问过
            S.push(e);
            child++;
            int lowv = dfs(v, u);
            lowu=min(lowu, lowv);                ///用后代更新
            if(lowv >= pre[u]){
                iscut[u]=true;
                bcc_cut++;bcc[bcc_cut].clear();   ///注意 bcc从1开始
                for(;;){
                    Edge x=S.top();S.pop();
                    if(bccno[x.u] != bcc_cut){bcc[bcc_cut].push_back(x.u);bccno[x.u]=bcc_cut;}
                    if(bccno[x.v] != bcc_cut){bcc[bcc_cut].push_back(x.v);bccno[x.v]=bcc_cut;}
                    if(x.u==u&&x.v==v)break;
                }
            }
        }
        else if(pre[v] < pre[u] && v !=fa){
            S.push(e);
            lowu = min(lowu,pre[v]);
        }
    }
    if(fa < 0 && child == 1) iscut[u] = 0;
    return lowu;
}
void find_bcc(int n){
    memset(pre, 0, sizeof(pre));
    memset(iscut, 0, sizeof(iscut));
    memset(bccno, 0, sizeof(bccno));
    dfs_clock = bcc_cut = 0;
    for(int i = 0; i < n;i++)
        if(!pre[i])dfs(i,-1);
}

求无向图的桥和割点

#include<iostream>
using namespace std;
#include<cstdio>
#include<cstring>
#include<vector>
#define N 201
vector<int>G[N];
int n,m,low[N],dfn[N];
bool is_cut[N];
int father[N];
int tim=0;
void input()
{
    scanf("%d%d",&n,&m);
    int a,b;
    for(int i=1;i<=m;++i)
    {
        scanf("%d%d",&a,&b);
        G[a].push_back(b);/*邻接表储存无向边*/
        G[b].push_back(a);
    }
}
void Tarjan(int i,int Father)
{
    father[i]=Father;/*记录每一个点的父亲*/
    dfn[i]=low[i]=tim++;
    for(int j=0;j<G[i].size();++j)
    {
        int k=G[i][j];
        if(dfn[k]==-1)
        {
            Tarjan(k,i);
            low[i]=min(low[i],low[k]);
        }
        else if(Father!=k)/*假如k是i的父亲的话，那么这就是无向边中的重边，有重边那么一定不是桥*/
            low[i]=min(low[i],dfn[k]);//dfn[k]可能！=low[k]，所以不能用low[k]代替dfn[k],否则会上翻过头了。
    }
}
void count()
{
    int rootson=0;
    Tarjan(1,0);
    for(int i=2;i<=n;++i)
    {
        int v=father[i];
        if(v==1)
        rootson++;/*统计根节点子树的个数，根节点的子树个数>=2,就是割点*/
        else{
            if(low[i]>=dfn[v])/*割点的条件*/
            is_cut[v]=true;
        }
    }
    if(rootson>1)
    is_cut[1]=true;
    for(int i=1;i<=n;++i)
    if(is_cut[i])
    printf("%d\n",i);
    for(int i=1;i<=n;++i)
    {
        int v=father[i];
        if(v>0&&low[i]>dfn[v])/*桥的条件*/
        printf("%d,%d\n",v,i);
    }
    
}
int main()
{
    input();
    memset(dfn,-1,sizeof(dfn));
    memset(father,0,sizeof(father));
    memset(low,-1,sizeof(low));
    memset(is_cut,false,sizeof(is_cut));
    count();
    return 0;
}

无向图的强连通分量/边双

int Laxt[maxn<<1],Next[maxn<<1],To[maxn<<1],cnt;
void add(int u,int v){
    Next[++cnt]=Laxt[u];
    Laxt[u]=cnt;To[cnt]=v;
}
int low[maxn],dfn[maxn],times,q[maxn],head,scc_cnt,scc[maxn];

void tarjan(int u,int f){
    dfn[u]=low[u]=++times;
    q[++head]=u;
    for(int i=Laxt[u];i;i=Next[i]){
        if(To[i]==f)continue;
        if(!dfn[To[i]]){
            tarjan(To[i],u);
            low[u]=min(low[u],low[To[i]]);
        }
        else low[u]=min(low[u],dfn[To[i]]);
    }
    if(low[u]==dfn[u]){
        scc_cnt++;
        while(true){
            int x=q[head--];
            scc[x]=scc_cnt;
            if(x==u)break;
        }
    }
}

有向图的强连通分量

vector<int>G[maxn];
int pre[maxn],lowlink[maxn],sccno[maxn],dfs_clock,scc_cnt;
stack<int>S;
inline void init(int n){
    for (int i = 0; i < n; i++) G[i].clear();
}
inline void add_edge(int u, int v) { G[u].push_back(v); }
void dfs(int u){
    pre[u]=lowlink[u]=++dfs_clock;
    S.push(u);
    for(int i=0;i<G[u].size();i++){
        int v=G[u][i];
        if(!pre[v]){
            dfs(v);
            lowlink[u]=min(lowlink[u],lowlink[v]);
        }
        else if(!sccno[v]){
            lowlink[u]=min(lowlink[u],pre[v]);
        }
    }
    if(lowlink[u]==pre[u]){
        scc_cnt++;
        for(;;){
            int x=S.top();S.pop();
            sccno[x]=scc_cnt;
            if(x==u)break;
        }
    }
}
void find_scc(int n){
    dfs_clock=scc_cnt=0;
    memset(sccno,0,sizeof(sccno));
    memset(pre,0,sizeof(pre));
    for(int i=0;i<n;i++)
        if(!pre[i])dfs(i);
}

2-SAT匹配

struct TwoSAT{
    int n;
    vector<int> G[maxn*2];
    bool mark[maxn*2];
    int S[maxn*2],c;

    bool dfs(int x){
        if(mark[x^1])return false;
        if(mark[x])return true;
        mark[x]=true;
        S[c++]=x;
        for(int i=0;i<G[x].size();i++)
            if(!dfs(G[x][i]))return false;
        return true;
    }

    void init(int n){
        this->n=n;
        for(int i=0;i<n*2;i++)G[i].clear();
        memset(mark,0,sizeof(mark));
    }
    /// x=xval or y= yval;
    void add_caluse(int x,int xval,int y,int yval){
        x=x*2+xval;
        y=y*2+yval;
        G[x^1].push_back(y);///如果x为真 那么y必须为假;
        G[y^1].push_back(x);///如果y为真 那么x必须为假;
    }

    bool solve(){
        for(int i=0;i<n*2;i+=2)
        if(!mark[i]&&!mark[i+1]){
            c=0;
            if(!dfs(i)){
                while(c>0)mark[S[--c]]=false;
                if(!dfs(i+1))return false;
            }
        }
        return true;
    }
};

最短路

Dijkstra +单源最短路+记录路径O(mlogn)

struct Edge{
    int from,to,dist;
};
struct HeapNode{
    int d,u;
    bool operator <(const HeapNode& rhs)const{
        return d>rhs.d;
    }
};
struct Dijkstra{
    int n,m;              ///点数和边数  点编号0~N-1
    vector<Edge>edges;    ///边列表
    vector<int>G[maxn];   ///每个节点出发的边编号
    bool done[maxn];      /// 是否已永久标号
    int d[maxn];          /// s到各个点的距离
    int p[maxn];          /// 最短路中的上一条边

    void init(int n){
        this->n=n;
        for(int i=0;i<n;i++)G[i].clear();
        edges.clear();
    }
    void AddEdge(int from,int to,int dist){ ///无向图调用两次
        edges.push_back((Edge){from,to,dist});
        m=edges.size();
        G[from].push_back(m-1);
    }
    void dijkstra(int s){
        priority_queue<HeapNode>Q;
        for(int i=0;i<n;i++)d[i]=inf;
        d[s]=0;
        memset(done,0,sizeof(done));
        Q.push((HeapNode){0,s});
        while(!Q.empty()){
            HeapNode x=Q.top();Q.pop();
            int u=x.u;
            if(done[u])continue;
            done[u]=true;
            for(int i=0;i<G[u].size();i++){
                Edge& e=edges[G[u][i]];
                if(d[e.to]>d[u]+e.dist){
                    d[e.to]=d[u]+e.dist;
                    p[e.to]=G[u][i];
                    Q.push((HeapNode){d[e.to],e.to});
                }
            }
        }
    }
    /// dist[i]为s到i的距离，paths[i]为s到i的最短路径（经过的结点列表，包括s和t）
    void GetShortestPaths(int s,int* dist,vector<int>* paths){///paths是二维链表
        dijkstra(s);
        for(int i=0;i<n;i++){
            dist[i]=d[i];
            paths[i].clear();
            int t=i;
            paths[i].push_back(t);
            while(t!=s){
                paths[i].push_back(edges[p[t]].from);
                t=edges[p[t]].from;
            }
            reverse(paths[i].begin(),paths[i].end());
        }
    }
};

BellmanFord （单源最短路判负环）O(nm)

struct Edge
{
    int from, to;
    int dist;
    Edge() {}
    Edge(int u, int v, int d) : from(u), to(v), dist(d) {}
};
struct BellmanFord{
    int n,m;
    vector<Edge>edges;
    vector<int> G[maxn];
    bool inq[maxn]; /// 是否在队列中
    int d[maxn];    /// s到各个点的距离  double 要改成double类型
    int p[maxn];    /// 最短路中的上一条弧
    int cnt[maxn];  /// 进队次数
    void init(int n){
        this->n=n;
        for(int i=0;i<n;i++)G[i].clear();
        edges.clear();
    }
    void AddEdge(int from, int to, int dist)
    {
        edges.emplace_back(from, to, dist);
        m = edges.size();
        G[from].push_back(m - 1);
    }
    bool bellmanford(int s){
        queue<int>Q;
        memset(inq,0,sizeof(inq));
        memset(cnt,0,sizeof(cnt));
        for(int i = 0; i < n; i++) { d[i] = 0; inq[0] = true; Q.push(i); } ///如果只判负环用这个
        //for(int i=0;i<n;i++)d[i]=inf;
        //d[s]=0;inq[s]=true;Q.push(s);
        while(!Q.empty()){
            int u=Q.front();
            Q.pop();
            inq[u]=false;
            for(auto& id:G[u]){
                Edge& e=edges[id];
                if(d[u]<inf && d[e.to]>d[u]+e.dist){
                    d[e.to]=d[u] + e.dist;
                    p[e.to]=id;
                    if(!inq[e.to]){
                        Q.push(e.to);
                        inq[e.to]=true;
                        if(++cnt[e.to]>n)return true;
                    }
                }
            }
        }
        return false;
    }
};

Floyd 多源最短路 O(n^3)

typedef struct{
    char vertex[maxn];        //顶点表
    int edges[maxn][maxn];    //邻接矩阵,可看做边表
    int n,e;                  //图中当前的顶点数和边数
}MGraph;

void Floyd(MGraph g){
    int A[maxn][maxn];
    int path[maxn][maxn];
    int i,j,k,n=g.n;
    for(i=0;i<n;i++)
    for(j=0;j<n;j++){
        A[i][j]=g.edges[i][j];
        path[i][j]=-1;
    }
    for(k=0;k<n;k++)
    for(i=0;i<n;i++)
    for(j=0;j<n;j++)
    if(A[i][j]>(A[i][k]+A[k][j])){
        A[i][j]=A[i][k]+A[k][j];
        path[i][j]=k;
    }
}

FLoyd 判最小环

    ///算法思想：如果存在最小环，会在编号最大的点u更新最短路径前找到这个环，发现的方法是，更新最短路径前，遍历i,j点对，一定会发现某对i到j的最短路径长度dis[i][j]+mp[j][u]+mp[u][i] != INF,这时i,j是图中挨着u的两个点，因为在之前最短路更新过程中，u没有参与更新，所以dis[i][j]所表示的路径中不会出现u，如果成立，则一定是一个环。用Floyd算法来实现。但是对于负环此算法失效，因为有负环时，dis[i][j]已经不能保证i到j的路径上不会经过同一个点多次了。
for(int k=1;k<=n;k++){
        for(int i=1;i<k;i++){
            for(int j=i+1;j<k;j++){
                mi=min(dis[i][j]+mp[j][k]+mp[k][i],mi);
            }
        }
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                if(dis[i][j]>(dis[i][k]+dis[k][j])){
                    dis[i][j]=dis[i][k]+dis[k][j];
                }
            }
        }
    }

Floyd 判环(龟兔赛跑算法)

（1）求环

初始状态下，假设已知某个起点节点为节点S。现设两个指针t和h，将它们均指向S。

同时让t和h往前推进，h的速度为t的2倍），直到h无法前进，即到达某个没有后继的节点时，就可以确定从S出发不会遇到环。反之当t与h再次相遇时，就可以确定从S出发一定会进入某个环，设其为环C。（h和t推进的步数差是环长的倍数）

（2）求环的长度

上述算法刚判断出存在环C时，t和h位于同一节点，设其为节点M。仅需令h不动，而t不断推进，最终又会返回节点M，统计这一次t推进的步数，就是环C的长度。

（3）求环的起点

为了求出环C的起点，只要令h仍均位于节点M，而令t返回起点节点S。随后，同时让t和h往前推进，且速度相同。持续该过程直至t与h再一次相遇，此相遇点就是环C的一个起点。

why？

假设出发起点到环起点的距离为m，已经确定有环，环的周长为n，（第一次）相遇点距离环的起点的距离是k。那么当两者相遇时，慢指针（t）移动的总距离i = m + a * n + k，快指针（h）的移动距离为2i，2i = m + b * n + k。其中，a和b分别为t和h在第一次相遇时转过的圈数。让两者相减（快减慢），那么有i = (b - a) * n。即i是圈长度的倍数。

将一个指针移到出发起点S，另一个指针仍呆在相遇节点M处两者同时移动，每次移动一步。当第一个指针前进了m，即到达环起点时，另一个指针距离链表起点为i + m。考虑到i为圈长度的倍数，可以理解为指针从链表起点出发，走到环起点，然后绕环转了几圈，所以第二个指针也必然在环的起点。即两者相遇点就是环的起点。

最小生成树

有向最小生成树（朱刘算法)

/// 固定根的最小树型图，邻接矩阵写法
struct MDST{
    int n;
    int w[maxn][maxn];    ///边权
    int vis[maxn];        ///访问标记，仅用来判断无解
    int ans;              ///计算答案
    int removed[maxn];    ///每个点是否被删除
    int cid[maxn];        ///所在圈编号
    int pre[maxn];        ///最小入边的起点
    int iw[maxn];         ///最小入边的权值
    int max_cid;          ///最大圈编号

    void init(int n){
        this->n=n;
        for(int i=0;i<n;i++)
            for(int j=0;j<n;j++)w[i][j]=inf;
    }
    void AddEdge(int u,int v,int cost){
        w[u][v]=min(w[u][v],cost);  ///重边取权值最小的
    }

    ///从s出发能到达多少个结点
    int dfs(int s){
        int ans=1;
        vis[s]=1;
        for(int i=0;i<n;i++)if(!vis[i]&&w[s][i]<inf)ans+=dfs(i);
        return ans;
    }
    ///从u出发沿着pre指针找圈
    bool cycle(int u){
        max_cid++;
        int v=u;
        while(cid[v]!=max_cid){cid[v]=max_cid;v=pre[v];}
        return v==u;
    }
    /// 计算u的最小入弧，入弧起点不得在圈c中
    void update(int u){
        iw[u]=inf;
        for(int i=0;i<n;i++)
        if(!removed[i]&&w[i][u]<iw[u]){
            iw[u]=w[i][u];
            pre[u]=i;
        }
    }
    ///根节点为s,如果失败返回false
    bool solve(int s){
        memset(vis,0,sizeof(vis));
        if(dfs(s)!=n)return false;
        memset(removed,0,sizeof(removed));
        memset(cid,0,sizeof(cid));
        for(int u=0;u<n;u++)update(u);
        pre[s]=s;iw[s]=0;      /// 根结点特殊处理
        ans=max_cid=0;
        for(;;){
            bool have_cycle=false;
            for(int u=0;u<n;u++)if(u!=s&&!removed[u]&&cycle(u)){
                have_cycle=true;
                /// 以下代码缩圈，圈上除了u之外的结点均删除
                int v=u;
                do{
                    if(v!=u)removed[v]=1;
                    ans+=iw[v];
                    /// 对于圈外点i，把边i->v改成i->u（并调整权值）；v->i改为u->i
                    /// 注意圈上可能还有一个v'使得i->v'或者v'->i存在，因此只保留权值最小的i->u和u->i
                    for(int i=0;i<n;i++)if(cid[i]!=cid[u]&&!removed[i]){
                        if(w[i][v]<inf)w[i][u]=min(w[i][u],w[i][v]-iw[v]);
                        w[u][i]=min(w[u][i],w[v][i]);
                        if(pre[i]==v)pre[i]=u;
                    }
                    v=pre[v];
                }while(v!=u);
                update(u);
                break;
            }
            if(!have_cycle)break;
        }
        for(int i=0;i<n;i++)
            if(!removed[i])ans+=iw[i];
        return true;
    }
};

二分图

理论

1.一个二分图中的最大匹配数等于这个图中的最小点覆盖数
2.最小路径覆盖 =|G|-最大匹配数
2.2 可重复先floyd再匹配
3.二分图最大独立集 = 顶点数-二分图最大匹配
  独立集: 图中任意两个顶点都不相连的顶点集合。
4.二分图的最大团=补图的最大独立集

二分图判断

color[maxn];
bool bipartite(int u){
    for(int i = 0;i < G[u].size(); i++){
        int v =G[u][i];
        if(color[v] == color[u])return false;
        if(!color[v]){
            color[v] = 3 - color[u];
            if(!bipartite(v,b))return false;
        }
    }
    return true;
}

匈牙利算法(dfs+bfs)

bool dfs(int u){
    for(int i=1;i<=n;i++){
        if(G[u][i]&&!vis[i]){
            vis[i]=true;
            if(!P[i]||dfs(P[i])){
                P[i]=u;return true;
            }
        }
    }
    return false;
}
        int ans=0;
        for(int i=1;i<=n;i++){
            memset(vis,false,sizeof(vis));
            if(dfs(i))ans++;
        }
/**************************/
int G[550][550];
bool vis[550];
int lefts[550],rights[550],pre[550];
int mark_rights[550];
int n;
int bfs(){
    memset(lefts,-1,sizeof(lefts));
    memset(rights,-1,sizeof(rights));
    int ans=0;
    for(int i=1;i<=n;i++){
        queue<int>q;
        q.push(i);
        bool flag=false;
        memset(mark_rights,0,sizeof(mark_rights));
        memset(pre,0,sizeof(pre));
        while(!q.empty()){
            int u=q.front();q.pop();
            for(int v=1;v<=n;v++){
                if(G[u][v]&&!mark_rights[v]){
                    mark_rights[v]=1;
                    if(rights[v]==-1){
                        flag=1;
                        int sl=u,sr=v;
                        while(sl!=0){
                            int st=lefts[sl];
                            lefts[sl]=sr;rights[sr]=sl;
                            sl=pre[sl];sr=st;
                        }
                        break;
                    }
                    else{
                        pre[rights[v]]=u;
                        q.push(rights[v]);
                    }
                }
            }
            if(flag)break;
        }
        if(flag)ans++;
    }
    return ans;
}

HK算法(优化匈牙利(√N*M))

const int maxn=3300+50;
const int inf=1e9;      //距离初始值
int bmap[maxn][maxn];   //二分图
int cx[maxn];           //表示左集合i顶点所匹配的右端点
int cy[maxn];           //右集合
int nx,ny,dx[maxn],dy[maxn],dis;
bool mark[maxn];
bool bfs(){
    queue<int>Q;
    dis=inf;
    memset(dx,-1,sizeof(dx));
    memset(dy,-1,sizeof(dy));
    for(int i=1;i<=nx;i++){
        if(cx[i]==-1)Q.push(i),dx[i]=0;
    }
    while(!Q.empty()){
        int u=Q.front();Q.pop();
        if(dx[u]>dis)break;
        for(int v=1;v<=ny;v++){
            if(bmap[u][v]&&dy[v]==-1){
                dy[v]=dx[u]+1;
                if(cy[v]==-1)dis=dy[v];
                else{
                    dx[cy[v]]=dy[v]+1;
                    Q.push(cy[v]);
                }
            }
        }
    }
    return dis!=inf;
}
int dfs(int u){
    for(int v=1;v<=ny;v++){
        if(!mark[v]&&bmap[u][v]&&dy[v]==dx[u]+1){
            mark[v]=1;
            if(cy[v]!=-1&&dy[v]==dis)continue;
            if(cy[v]==-1||dfs(cy[v])){
                cy[v]=u;cx[u]=v;
                return 1;
            }
        }
    }
    return 0;
}
int MaxMatch(){
    int res=0;
    memset(cx,-1,sizeof(cx));
    memset(cy,-1,sizeof(cy));
    while(bfs()){
        memset(mark,0,sizeof(mark));
        for(int i=1;i<=nx;i++){
            if(cx[i]==-1)res+=dfs(i);
        }
    }
    return res;
}

二分图最大基数匹配

/// 二分图最大基数匹配
struct BPM{
    int n,m;    /// 左右顶点个数
    vector<int>G[maxn]; /// 邻接表
    int left[maxn];    /// left[i]为右边第i个点的匹配点编号，-1表示不存在
    bool T[maxn];       /// T[i]为右边第i个点是否已标记

    int right[maxn];        /// 求最小覆盖用
    bool S[maxn];           /// 求最小覆盖用

    void init(int n,int m){
        this->n=n;
        this->m=m;
        for(int i=0;i<n;i++)G[i].clear();
    }

    void AddEdge(int u,int v){
        G[u].push_back(v);
    }

    bool match(int u){
        S[u]=true;
        for(int i=0;i<G[u].size();i++){
            int v=G[u][i];
            if(!T[v]){
                T[v]=true;
                if(left[v]==-1||match(left[v])){
                    left[v]=u;
                    right[u]=v;
                    return true;
                }
            }
        }
        return false;
    }
    /// 求最大匹配
    int solve(){
        memset(left,-1,sizeof(left));
        memset(right,-1,sizeof(right));
        int ans=0;
        for(int u=0;u<n;u++){
            memset(S,0,sizeof(S));
            memset(T,0,sizeof(T));
            if(match(u))ans++;
        }
        return ans;
    }
    /// 求最小覆盖。X和Y为最小覆盖中的点集
    int mincover(vector<int>& X,vector<int>& Y){
        int ans=solve();
        memset(S,0,sizeof(S));
        memset(T,0,sizeof(T));
        for(int u=0;u<n;u++)
            if(right[u]==-1)match(u);
        for(int u=0;u<n;u++)
            if(!S[u])X.push_back(u);
        for(int v=0;v<n;v++)
            if(T[v])Y.push_back(v);
        return ans;
    }
};

二分图最大权匹配(KM算法)

int g[150][150];  ///存图
int nx,ny; /// 两边点数
bool visx[maxn],visy[maxn];
int slack[maxn];
int linker[maxn];   ///y中各点匹配状态
int lx[maxn],ly[maxn]; /// x,y中的点标号
bool dfs(int x){
    visx[x]=true;
    for(int y=0;y<ny;y++){
        if(visy[y])continue;
        int tmp=lx[x]+ly[y]-g[x][y];
        if(tmp==0){
            visy[y]=true;
            if(linker[y]==-1||dfs(linker[y])){
                linker[y]=x;return true;
            }
        }
        else if(slack[y]>tmp)slack[y]=tmp;
    }
    return false;
}
int KM(){
    memset(linker,-1,sizeof(linker));
    memset(ly,0,sizeof(ly));
    for(int i=0;i<nx;i++){
        lx[i]=-inf;
        for(int j=0;j<ny;j++){
            if(g[i][j]>lx[i])lx[i]=g[i][j];
        }
    }
    for(int x=0;x<nx;x++){
        for(int i=0;i<ny;i++)slack[i]=inf;
        while(true){
            memset(visx,false,sizeof(visx));
            memset(visy,false,sizeof(visy));
            if(dfs(x))break;
            int d=inf;
            for(int i=0;i<ny;i++)
                if(!visy[i]&&d>slack[i])d=slack[i];
            for(int i=0;i<nx;i++)
                if(visx[i])lx[i]-=d;
            for(int i=0;i<ny;i++)
                if(visy[i])ly[i]+=d;
                else slack[i]-=d;
        }
    }
    int res=0;
    for(int i=0;i<ny;i++)
        if(linker[i]!=-1)res+=g[linker[i]][i];
    return res;
}

bfs实现的KM

const int N=2e2+50;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
int val[N][N];
ll lx[N],ly[N];
int linky[N];
ll pre[N];
bool vis[N];
bool visx[N],visy[N];
ll slack[N];
int n;
void bfs(int k){
    ll px, py = 0,yy = 0, d;
    memset(pre, 0, sizeof(ll) * (n+2));
    memset(slack, inf, sizeof(ll) * (n+2));
    linky[py]=k;
    do{
        px = linky[py],d = INF, vis[py] = 1;
        for(int i = 1; i <= n; i++)
            if(!vis[i]){
                if(slack[i] > lx[px] + ly[i] - val[px][i])
                    slack[i] = lx[px] + ly[i] -val[px][i], pre[i]=py;
                if(slack[i]<d) d=slack[i],yy=i;
            }
        for(int i = 0; i <= n; i++)
            if(vis[i]) lx[linky[i]] -= d, ly[i] += d;
            else slack[i] -= d;
        py = yy;
    }while(linky[py]);
    while(py) linky[py] = linky[pre[py]] , py=pre[py];
}
void KM(){
    memset(lx, 0, sizeof(int)*(n+2));
    memset(ly, 0, sizeof(int)*(n+2));
    memset(linky, 0, sizeof(int)*(n+2));
    for(int i = 1; i <= n; i++)
        memset(vis, 0, sizeof(bool)*(n+2)), bfs(i);
}
        ll ans=0;
        KM();
        for(int i=1;i<=n;i++)ans+=lx[i]+ly[i];

网络流

理论

建模技巧

##二分图带权最大独立集。
给出一个二分图，每个结点上有一个正权值。要求选出一些点，使得这些点之间没有边相连，且权值和最大。

解：在二分图的基础上添加源点 S 和汇点 T，然后从 S 向所有 X 集合中的点连一条边，所有 Y 集合中的点向 T 连一条边，容量均为该点的权值。X 结点与 Y 结点之间的边的容量均为无穷大。这样，对于图中的任意一个割，将割中的边对应的结点删掉就是一个符合要求的解，权和为所有权减去割的容量。因此，只需要求出最小割，就能求出最大权和。

##公平分配问题。
把 m 个任务分配给 n 个处理器。其中每个任务有两个候选处理器，可以任选一个分配。要求所有处理器中，任务数最多的那个处理器所分配的任务数尽量少。不同任务的候选处理器集 {p1, p2} 保证不同。

解：本题有一个比较明显的二分图模型，即 X 结点是任务，Y 结点是处理器。二分答案 x，然后构图，首先从源点S 出发向所有的任务结点引一条边，容量等于 1，然后从每个任务结点出发引两条边，分别到达它所能分配到的两个处理器结点，容量为 1，最后从每个处理器结点出发引一条边到汇点 T，容量为 x，表示选择该处理器的任务不能超过 x。这样网络中的每个单位流量都是从 S 流到一个任务结点，再到处理器结点，最后到汇点 T。只有当网络中的总流量等于
m 时才意味着所有任务都选择了一个处理器。这样，我们通过 O(log m) 次最大流便算出了答案。

##区间 k 覆盖问题。
数轴上有一些带权值的左闭右开区间。选出权和尽量大的一些区间，使得任意一个数最多被 k 个区间覆盖
解：本题可以用最小费用流解决，构图方法是把每个数作为一个结点，然后对于权值为 w 的区间 [u, v) 加边 u→v，容量为 1，费用为 −w。再对所有相邻的点加边 i→i + 1，容量为 k，费用为 0。最后，求最左点到最右点的最小费用最大流即可，其中每个流量对应一组互不相交的区间。如果数值范围太大，可以先进行离散化。

##最大闭合子图。
给定带权图 G（权值可正可负），求一个权和最大的点集，使得起点在该点集中的任意弧，终点也在该点集中。
解：新增附加源 s 和附加汇 t，从 s 向所有正权点引一条边，容量为权值；从所有负权点向汇点引一条边，容量为权值的相反数。求出最小割以后，S − {s} 就是最大闭合子图。

##最大密度子图。
给出一个无向图，找一个点集，使得这些点之间的边数除以点数的值（称为子图的密度）最大。
解：如果两个端点都选了，就必然要选边，这就是一种推导。如果把每个点和每条边都看成新图中的结点，可以把问题转化为最大闭合子图。

假设答案为k ，则要求解的问题是：边/点=K最大
选出一个合适的点集 V 和边集 E，令(|E|−k∗|V|)取得最大值。
所谓“合适”是指满足如下限制：若选择某条边，则必选择其两端点。
建图:
以原图的边作为左侧顶点，权值为1；
原图的点作为右侧顶点，权值为+k。
若原图中存在边 (u,v)，则新图中添加两条边 ([uv]−>u),([uv]−>v)，转换为最大权闭合子图。

## 二分图的最小点权覆盖集算法
在原图点集的基础上增加源 和汇 ；将每条二分图的边 s ,u v E ∈t 替换为容量=∞的有向边 , 把所有的X连线源，所有的Y连线汇容量为点权，

## 最大点权独立集 = V-最小点权覆盖

上下界网络流建图方法

## 记号说明
• f(u, v) 表示 u → v 的实际流量
• b(u, v) 表示 u → v 的流量下界
• c(u, v) 表示 u → v 的流量上界
##无源汇可行流
 建图
	• 新建附加源点 S 和 T
	• 原图中的边 u → v，限制为 [b, c]，建边 u → v，容量为 c − b
	• 记 d(i) = ∑b(u, i) −∑b(i, v)
	• 若 d(i) > 0，建边 S → i，流量为 d(i)
	• 若 d(i) < 0，建边 i → T，流量为 −d(i)
   
求解
	• 跑 S → T 的最大流，如果满流，则原图存在可行流。
	• 此时，原图中每一条边的流量为新图中对应边的流量加上这条边的下界。
	
##有源汇可行流
建图
	• 在原图中建边 t → s，流量限制为 [0, +∞)，这样就改造成了无源汇的网络流图。
	• 之后就可以像求解无源汇可行流一样建图了。
求解 同无源汇可行流

##有源汇最大流
建图 同有源汇可行流
求解
	• 先跑一遍 S → T 的最大流，求出可行流
	• 记此时 ∑f(s, i) = sum1
	• 将 t → s 这条边拆掉，在新图上跑 s → t 的最大流
	• 记此时 ∑f(s, i) = sum2
	• 最终答案即为 sum1 + sum2
##有源汇最小流
建图 同有源汇可行流
求解
	• 先跑一遍 S → T 的最大流，求出可行流
	• 记此时 ∑f(s, i) = sum1
	• 将 t → s 这条边拆掉，在新图上跑 t → s 的最大流f
	• 最终答案即为 sum1 - f
	这个可以理解成通过最大化退流量来使得流量最小。
##有源汇费用流
建图
	• 新建附加源点 S 和 T
	• 原图中的边 u → v，限制为 [b, c]，费用为 cost，建边 u → v，容量为 c − b，费用为 cost
• 记 d(i) = ∑b(u, i) −
∑b(i, v)
	• 若 d(i) > 0，建边 S → i，流量为 d(i)，费用为 0
	• 若 d(i) < 0，建边 i → T，流量为 −d(i)，费用为 0
	• 建边 t → s，流量为 +∞，费用为 0。
求解
	• 跑 S → T 的最小费用最大流
	• 答案为求出的费用加上原图中边的下界乘以边的费用

Edge

struct Edge
{
    int from, to, cap, flow;
    Edge(int u, int v, int c, int f)
        : from(u), to(v), cap(c), flow(f) {}
};
// ---
// 费用流
// ---
struct Edge
{
    int from, to, cap, flow, cost;
    Edge(int u, int v, int c, int f, int w)
        : from(u), to(v), cap(c), flow(f), cost(w) {}
};

EdmondKarp

const int maxn = "Edit";
struct EdmonsKarp //时间复杂度O(v*E*E)
{
    int n, m;
    vector<Edge> edges;  //边数的两倍
    vector<int> G[maxn]; //邻接表，G[i][j]表示节点i的第j条边在e数组中的序号
    int a[maxn];         //起点到i的可改进量
    int p[maxn];         //最短路树上p的入弧编号
    void init(int n)
    {
        for (int i = 0; i < n; i++) G[i].clear();
        edges.clear();
    }
    void AddEdge(int from, int to, int cap)
    {
        edges.emplace_back(from, to, cap, 0);
        edges.emplace_back(to, from, 0, 0); //反向弧
        m = edges.size();
        G[from].push_back(m - 2);
        G[to].push_back(m - 1);
    }
    int Maxflow(int s, int t)
    {
        int flow = 0;
        for (;;)
        {
            memset(a, 0, sizeof(a));
            queue<int> q;
            q.push(s);
            a[s] = INF;
            while (!q.empty())
            {
                int x = q.front();
                q.pop();
                for (int i = 0; i < G[x].size(); i++)
                {
                    Edge& e = edges[G[x][i]];
                    if (!a[e.to] && e.cap > e.flow)
                    {
                        p[e.to] = G[x][i];
                        a[e.to] = min(a[x], e.cap - e.flow);
                        q.push(e.to);
                    }
                }
                if (a[t]) break;
            }
            if (!a[t]) break;
            for (int u = t; u != s; u = edges[p[u]].from)
            {
                edges[p[u]].flow += a[t];
                edges[p[u] ^ 1].flow -= a[t];
            }
            flow += a[t];
        }
        return flow;
    }
};

Dinic

const int maxn = "Edit";
struct Dinic
{
    int n, m, s, t;      //结点数，边数（包括反向弧），源点编号和汇点编号
    vector<Edge> edges;  //边表。edge[e]和edge[e^1]互为反向弧
    vector<int> G[maxn]; //邻接表，G[i][j]表示节点i的第j条边在e数组中的序号
    bool vis[maxn];      //BFS使用
    int d[maxn];         //从起点到i的距离
    int cur[maxn];       //当前弧下标
    void init(int n)
    {
        this->n = n;
        for (int i = 0; i < n; i++) G[i].clear();
        edges.clear();
    }
    void AddEdge(int from, int to, int cap)
    {
        edges.emplace_back(from, to, cap, 0);
        edges.emplace_back(to, from, 0, 0);
        m = edges.size();
        G[from].push_back(m - 2);
        G[to].push_back(m - 1);
    }
    bool BFS()
    {
        memset(vis, 0, sizeof(vis));
        memset(d, 0, sizeof(d));
        queue<int> q;
        q.push(s);
        d[s] = 0;
        vis[s] = 1;
        while (!q.empty())
        {
            int x = q.front();
            q.pop();
            for (int i = 0; i < G[x].size(); i++)
            {
                Edge& e = edges[G[x][i]];
                if (!vis[e.to] && e.cap > e.flow)
                {
                    vis[e.to] = 1;
                    d[e.to] = d[x] + 1;
                    q.push(e.to);
                }
            }
        }
        return vis[t];
    }
    int DFS(int x, int a)
    {
        if (x == t || a == 0) return a;
        int flow = 0, f;
        for (int& i = cur[x]; i < G[x].size(); i++)
        { //从上次考虑的弧
            Edge& e = edges[G[x][i]];
            if (d[x] + 1 == d[e.to] && (f = DFS(e.to, min(a, e.cap - e.flow))) > 0)
            {
                e.flow += f;
                edges[G[x][i] ^ 1].flow -= f;
                flow += f;
                a -= f;
                if (a == 0) break;
            }
        }
        return flow;
    }
    int Maxflow(int s, int t)
    {
        this->s = s, this->t = t;
        int flow = 0;
        while (BFS())
        {
            memset(cur, 0, sizeof(cur));
            flow += DFS(s, INF);
        }
        return flow;
    }
    vector<int>Mincut(){ /// call this after maxflow
        vector<int>ans;
        for(int i=0;i<edges.size();i++){
            Edge& e=edges[i];
            if(vis[e.from]&&!vis[e.to]&&e.cap>0)ans.push_back(i);
        }
        return ans;
    }
};

ISAP

const int maxn = "Edit";
struct ISAP
{
    int n, m, s, t;      //结点数，边数（包括反向弧），源点编号和汇点编号
    vector<Edge> edges;  //边表。edges[e]和edges[e^1]互为反向弧
    vector<int> G[maxn]; //邻接表，G[i][j]表示结点i的第j条边在e数组中的序号
    bool vis[maxn];      //BFS使用
    int d[maxn];         //起点到i的距离
    int cur[maxn];       //当前弧下标
    int p[maxn];         //可增广路上的一条弧
    int num[maxn];       //距离标号计数
    void init(int n)
    {
        this->n = n;
        for (int i = 0; i < n; i++) G[i].clear();
        edges.clear();
    }
    void AddEdge(int from, int to, int cap)
    {
        edges.emplace_back(from, to, cap, 0);
        edges.emplace_back(to, from, 0, 0);
        int m = edges.size();
        G[from].push_back(m - 2);
        G[to].push_back(m - 1);
    }
    int Augumemt()
    {
        int x = t, a = INF;
        while (x != s)
        {
            Edge& e = edges[p[x]];
            a = min(a, e.cap - e.flow);
            x = edges[p[x]].from;
        }
        x = t;
        while (x != s)
        {
            edges[p[x]].flow += a;
            edges[p[x] ^ 1].flow -= a;
            x = edges[p[x]].from;
        }
        return a;
    }
    void BFS()
    {
        memset(vis, 0, sizeof(vis));
        memset(d, 0, sizeof(d));
        queue<int> q;
        q.push(t);
        d[t] = 0;
        vis[t] = 1;
        while (!q.empty())
        {
            int x = q.front();
            q.pop();
            int len = G[x].size();
            for (int i = 0; i < len; i++)
            {
                Edge& e = edges[G[x][i] ^ 1];
                if (!vis[e.from] && e.cap > e.flow)
                {
                    vis[e.from] = 1;
                    d[e.from] = d[x] + 1;
                    q.push(e.from);
                }
            }
        }
    }
    int Maxflow(int s, int t)
    {
        this->s = s;
        this->t = t;
        int flow = 0;
        BFS();
        memset(num, 0, sizeof(num));
        for (int i = 0; i < n; i++)
            if (d[i] < INF) num[d[i]]++;
        int x = s;
        memset(cur, 0);
        while (d[s] < n)
        {
            if (x == t)
            {
                flow += Augumemt();
                x = s;
            }
            int ok = 0;
            for (int i = cur[x]; i < G[x].size(); i++)
            {
                Edge& e = edges[G[x][i]];
                if (e.cap > e.flow && d[x] == d[e.to] + 1)
                {
                    ok = 1;
                    p[e.to] = G[x][i];
                    cur[x] = i;
                    x = e.to;
                    break;
                }
            }
            if (!ok) //Retreat
            {
                int m = n - 1;
                for (int i = 0; i < G[x].size(); i++)
                {
                    Edge& e = edges[G[x][i]];
                    if (e.cap > e.flow) m = min(m, d[e.to]);
                }
                if (--num[d[x]] == 0) break; //gap优化
                num[d[x] = m + 1]++;
                cur[x] = 0;
                if (x != s) x = edges[p[x]].from;
            }
        }
        return flow;
    }
};

MinCost MaxFlow

const int maxn = "Edit";
struct MCMF
{
    int n, m;
    vector<Edge> edges;
    vector<int> G[maxn];
    int inq[maxn]; //是否在队列中
    int d[maxn];   //bellmanford
    int p[maxn];   //上一条弧
    int a[maxn];   //可改进量
    void init(int n)
    {
        this->n = n;
        for (int i = 0; i < n; i++) G[i].clear();
        edges.clear();
    }
    void AddEdge(int from, int to, int cap, int cost)
    {
        edges.emplace_back(from, to, cap, 0, cost);
        edges.emplace_back(to, from, 0, 0, -cost);
        m = edges.size();
        G[from].push_back(m - 2);
        G[to].push_back(m - 1);
    }
    bool BellmanFord(int s, int t, int& flow, ll& cost)
    {
        for (int i = 0; i < n; i++) d[i] = INF;
        memset(inq, 0, sizeof(inq));
        d[s] = 0;
        inq[s] = 1;
        p[s] = 0;
        a[s] = INF;
        queue<int> q;
        q.push(s);
        while (!q.empty())
        {
            int u = q.front();
            q.pop();
            inq[u] = 0;
            for (int i = 0; i < G[u].size(); i++)
            {
                Edge& e = edges[G[u][i]];
                if (e.cap > e.flow && d[e.to] > d[u] + e.cost)
                {
                    d[e.to] = d[u] + e.cost;
                    p[e.to] = G[u][i];
                    a[e.to] = min(a[u], e.cap - e.flow);
                    if (!inq[e.to])
                    {
                        q.push(e.to);
                        inq[e.to] = 1;
                    }
                }
            }
        }
        if (d[t] == INF) return false; // 当没有可增广的路时退出
        flow += a[t];
        cost += (ll)d[t] * (ll)a[t];
        for (int u = t; u != s; u = edges[p[u]].from)
        {
            edges[p[u]].flow += a[t];
            edges[p[u] ^ 1].flow -= a[t];
        }
        return true;
    }
    int MincostMaxflow(int s, int t, ll& cost)
    {
        int flow = 0;
        cost = 0;
        while (BellmanFord(s, t, flow, cost));
        return flow;
    }
};

sap

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+50;
int S,T,From[maxn],Laxt[maxn],Next[maxn],To[maxn],Cap[maxn],cnt;
int vd[maxn],dis[maxn];
void add(int u,int v,int c){
    Next[++cnt]=Laxt[u];Laxt[u]=cnt;To[cnt]=v;Cap[cnt]=c;From[cnt]=u;
    Next[++cnt]=Laxt[v];Laxt[v]=cnt;To[cnt]=u;Cap[cnt]=0;From[cnt]=v;
}
int sap(int u,int flow,int limit){
    if(u==T||flow==0)return flow;
    int tmp,delta=0;
    for(int i=Laxt[u];i;i=Next[i]){
        int v=To[i];
        if(dis[u]==dis[v]+1&&Cap[i]){
            tmp=sap(v,min(flow-delta,Cap[i]),limit);
            Cap[i]-=tmp;Cap[i^1]+=tmp;delta+=tmp;
            if(dis[S]>=(limit)||delta==flow)return delta;
        }
    }
    vd[dis[u]]--;if(!vd[dis[u]])dis[S]=limit;
    vd[++dis[u]]++;
    return delta;
}
void init(int limit){
    cnt=1;
    for(int i=0;i<=limit;i++)Laxt[i]=dis[i]=vd[i]=0;
}

LCA

倍增

struct LCA{
    int n;
    int fa[maxn];       ///父亲数组
    int cost[maxn];     ///和父亲的费用
    int L[maxn];        ///层次(根节点为0)
    int anc[maxn][logmaxn];     /// anc[p][i]是结点p的第2^i级父亲。anc[i][0] = fa[i]
    int maxcost[maxn][logmaxn]; /// maxcost[p][i]是i和anc[p][i]的路径上的最大费用
    void preprocess(){
        for(int i=0;i<n;i++){
            anc[i][0]=fa[i];maxcost[i][0]=cost[i];
            for(int j=1;(1<<j)<n;j++)anc[i][j]=-1;
        }
        for(int j=1;(1<<j)<n;j++)
            for(int i=0;i<n;i++)
        if(anc[i][j-1]!=-1){
            int a=anc[i][j-1];
            anc[i][j]=anc[a][j-1];
            maxcost[i][j]=max(maxcost[i][j-1],maxcost[a][j-1]);
        }
    }
    /// 求p到q的路径上的最大权
    int query(int p,int q){
        int tmp,log,i;
        if(L[p]<L[q])swap(p,q);
        for(log=1;(1<<log)<=L[p];log++);log--;
        int ans=-inf;
        for(int i=log;i>=0;i--)
        if(L[p]-(1<<i)>=L[q]){ans=max(ans,maxcost[p][i]);p=anc[p][i];}

        if(p==q)return ans; ///LCA为p

        for(int i=log;i>=0;i--)
        if(anc[p][i]!=-1&&anc[p][i]!=anc[q][i]){
            ans=max(ans,maxcost[p][i]);p=anc[p][i];
            ans=max(ans,maxcost[q][i]);q=anc[q][i];
        }
        ans=max(ans,cost[p]);
        ans=max(ans,cost[q]);
        return ans; ///LCA为fa[p]（它也等于fa[q]）
    }
};

倍增简单写法

int mi[maxn][22],fa[maxn][22],dep[maxn];
void dfs(int now,int pre,int w,int deep){
    fa[now][0]=pre;
    mi[now][0]=w;
    if(pre==0)mi[now][0]=inf,fa[now][0]=now;
    dep[now]=deep;
    for(auto i:ve[now]){
        if(i.to==pre)continue;
        dfs(i.to,now,i.w,deep+1);
    }
}
void init(){
    for(int i=1;i<=20;i++)
    for(int j=1;j<=n;j++){
        int p=fa[j][i-1];
        fa[j][i]=fa[p][i-1];
        mi[j][i]=min(mi[j][i-1],mi[p][i-1]);
    }
}
int lca(int p,int q){
    if(dep[p]<dep[q])swap(p,q);
    int res=inf;
    for(int i=20;i>=0;i--)
        if(dep[fa[p][i]]>=dep[q])
        res=min(res,mi[p][i]),p=fa[p][i];
    if(p==q)return res;
    for(int i=20;i>=0;i--){
        if(fa[p][i]!=fa[q][i]){
            res=min(res,mi[p][i]);
            res=min(res,mi[q][i]);
            p=fa[p][i];q=fa[q][i];
        }
    }
    return min(res,min(mi[p][0],mi[q][0]));
}

RMQ写法

int d[maxn*2][20],dep[maxn],id[maxn],w[maxn],cnt; ///空间要开两倍多
int n,sum,rt,f[maxn],vis[maxn],luo,sz[maxn];
void init(){
    for(int i=1;i<=n;i++)
        G[i].clear(),vis[i]=f[i]=0;
    cnt=0;
}
void dfs(int u,int fa){
    dep[u]=dep[fa]+1;
    d[++cnt][0] = dep[u];
    id[u] = cnt;
    for(auto v:G[u]){
        if(v==fa)continue;
        dfs(v, u);
        d[++cnt][0]=dep[u];
    }
}
void rmq_init(){
    for(int i=1;i<=18;i++)
        for(int j=1;j+(1<<i)-1<=cnt;j++)
            d[j][i]=min(d[j][i-1],d[j+(1<<i-1)][i-1]);
}
int LCA(int x,int y){
    int l=id[x],r=id[y];
    if(l>r)swap(l,r);
    int k=log2(r-l+1);
    return min(d[l][k],d[r+1-(1<<k)][k]);
}
int dis(int x,int y){
    return dep[x]+dep[y]-2*LCA(x,y);
}

树上差分

点差分

//查询每个点没经过的次数
int sum[maxn],mx;
int dfs1(int u,int p){
    for(int i=Laxt[u];i;i=Next[i]){
        int v=To[i];if(v==p)continue;
        dfs1(v,u);sum[u]+=sum[v];
    }
    if(sum[u]>mx)mx=sum[u];
}
while(k--){
        int u,v;
        cin>>u>>v;
        sum[u]++;sum[v]++;
        int p=lca(u,v);
        sum[p]--;
        sum[fa[p][0]]--;
    }
dfs1(1,0);

边差分

//查询每个边的经过次数
//边传递给后一个节点
void dfs(int u,int pre){
    for(int i=Laxt[u];i;i=Next[i]){
        int v=To[i];
        if(v==pre)continue;
        dfs(v,u);
        num[u]+=num[v];
    }
}
bool check(int x){
    int k=0,now=0;
    for(int i=1;i<=n;i++)num[i]=0;
    for(int i=1;i<=m;i++){
        if(my[i].w<=x)continue;
        num[my[i].u]++;num[my[i].v]++;num[my[i].lca]-=2;
        k++;
    }
    dfs(1,0);
    for(int i=1;i<=n;i++)if(num[i]==k)now=max(now,value[i]);
    return my[m].w-now<=x;
}

数学

拉格朗日插值

普通n^2

ll n,k;
x[1]=1;x[2]=2;x[3]=3;x[4]=4;x[5]=5;
y[1]=1;y[2]=5;y[3]=15;y[4]=35;y[5]=70;
int t;n=5;
cin>>t;
while(t--){
    cin>>k;
    ll ans=0;
    for(int i=1;i<=n;i++){
        ll fz=y[i];
        ll fm=1;
        for(int j=1;j<=n;j++){
            if(i==j)continue;
            fz=fz*(k-x[j])%mod;
            fm=fm*(x[i]-x[j])%mod;
        }
        ans+=fz*ksm(fm,mod-2)%mod;
        ans%=mod;
        ans+=mod;ans%=mod;
    }
    cout<<ans<<endl;
}

x取连续时的插值法复杂度O(n)

 
int pv[]={0,1,5,15,35,70}; //前几项, 前面无效值用0占位
const int st=1,ed=5;           //使用上面数组下标为[st,ed]的数据
 
ll fac[ed+5],inv[ed+5],facinv[ed+5];
ll pre[ed+5],saf[ed+5];
 
//预处理: fac[]阶乘, inv[]逆元, facinv[]阶乘逆元
//只需要main函数内调用一次!
void init()
{
    fac[0]=inv[0]=facinv[0]=1;
    fac[1]=inv[1]=facinv[1]=1;
    for(int i=2;i<ed+3;++i)
    {
        fac[i]=fac[i-1]*i%mod;
        inv[i]=mod-(mod/i*inv[mod%i]%mod);
        facinv[i]=facinv[i-1]*inv[i]%mod;
    }
}
 
 
//计算第x0项的值
//复杂度O(ed-st)
ll cal(ll x0)
{
    int n=ed-st;
    x0=((x0%mod)+mod)%mod;
    pre[0]=((x0-st)%mod+mod)%mod;
    saf[n]=((x0-st-n)%mod+mod)%mod;
    for(int i=1;i<=n;++i)
    {
        pre[i]=((pre[i-1]*(x0-st-i))%mod+mod)%mod;
        saf[n-i]=((saf[n-i+1]*(x0-st-n+i))%mod+mod)%mod;
    }
    ll res=0;
    for(int i=0;i<=n;++i)
    {
        ll fz=1;
        if(i!=0)fz=fz*pre[i-1]%mod;
        if(i!=n)fz=fz*saf[i+1]%mod;
        ll fm=facinv[i]*facinv[n-i]%mod;
        if((n-i)&1)fm=mod-fm;
        (res+=pv[i+st]*(fz*fm%mod)%mod)%=mod;
    }
    return res;
}
 
int main()
{
    init();
    int t,n;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        printf("%d\n",cal(n));
    }
 
}

差分表

一些公式

//平方和公式 sigm（i^2）=n*(n+1)*(2n+1)/6
//皮克定理 多边形面积S = 多边形内整数点的个数 n + 多边形边上整数点的个数 / 2 - 1 
//边界的点数用gcd(a.x-b.x,a.y-b.y)计算
//当O点为原点时，根据向量的叉积计算公式，各个三角形的面积计算如下：
//S_OAB = 0.5*(A_x*B_y - A_y*B_x)   【(A_x，A_y)为A点的坐标】
//S_OBC = 0.5*(B_x*C_y - B_y*C_x)
/*
斯特林公式
 int digit_stirling(int n)///求n！的位数
{
     double PI=acos(double(-1));// PI的值=反余弦函数 -1.0为Pi， 1为0。
     double e=exp(double(1));//e的值
     return floor(log10(sqrt(2*PI*n))+n*log10(n/e))+1;
}
*/
//G[X]表示：1-X的数字和的总和；

//根据G[10^X]=45*X*10^(X-1);所以G[10^18]=45*18*10^17;
//等差数列求和：Sn=n*a1+n(n-1)d/2或Sn=n(a1+an)/2
//等比数列求和：Sn=a1*(1-q^n)/(1-q)=(a1-an*q)/(1-q)

莫比乌斯反演

$F(n)=\sum_{d|n}f(d)\\ f(n)=\sum_{d|n}\mu(d)F(\lfloor\frac{n}{d}\rfloor)$ $F(n)=\sum_{n|d}f(d)\\f(n)=\sum_{n|d}\mu(\frac{d}{n})F(d)$

组合数计数

    inv[0]=p[0]=1;
    for(int i=1;i<=n;i++)
        p[i]=p[i-1]*i%mod,inv[i]=ksm(p[i],mod-2);
}
ll cal(int n,int m){
    if(n<m)return 0LL;
    return p[n]*inv[n-m]%mod*inv[m]%mod;
}

卢卡斯定理

ll pow_mod(ll x, ll n, ll mod){
    ll res=1;
    while(n){
        if(n&1)res=res*x%mod;
        x=x*x%mod;
        n>>=1;
    }
    return res;
}
ll inv(ll a,ll p){return pow_mod(a,p-2,p);}
ll cal(ll a,ll b,ll p){
    if(a<b)return 0;
    if(b>a-b)b=a-b;
    ll fz=1,fm=1;
    for(ll i=0;i<b;i++){
        fz=fz*(a-i)%p;
        fm=fm*(i+1)%p;
    }
    return fz*inv(fm,p)%p;
}

ll lucas(ll a,ll b,ll p){
    if(b==0)return 1;
    return cal(a%p,b%p,p)*lucas(a/p,b/p,p)%p;
}

逆元

如果mod不是素数那么a关于mod的逆元是 a^(phi(mod)-1)

ExGcd求逆元

///返回 d=gcd(a,b); 和对应于等式 ax+by=d 中的 x,y
ll extend_gcd(ll a,ll b,ll &x,ll &y){
    if(a==0&&b==0)return -1;
    if(b==0){x=1;y=0;return a;}
    ll d=extend_gcd(b,a%b,y,x);
    y-=a/b*x;
    return d;
}
///ax=1(mod n)
ll mod_reverse(ll a,ll n){
    ll x,y;
    ll d=extend_gcd(a,n,x,y);
    if(d==1)return (x%n+n)%n;
    else return -1;
}

费马小定理

///a<mod 并且 p为素数
ll pow_mod(ll x, ll n, ll mod){
    ll res=1;
    while(n){
        if(n&1)res=res*x%mod;
        x=x*x%mod;
        n>>=1;
    }
    return res;
}
ll inv(ll a,ll p){return pow_mod(a,p-2,p);}

逆元线性筛

1 2	inv[1]=1; for (int i = 2; i < maxn; i++) inv[i] = inv[p % i] * (p - p / i) % p;

杜教筛

设需要计算的式子为：$[Math Processing Error]\sum_{i=1}^{n}f(i)（f(i)为积性函数）$

我们构造两个积性函数$h$和$g$。使得$h=f∗g$

现在我们开始求$\sum_{i=1}^{n}h(i)$

记$[Math Processing Error]S(n)=\sum_{i=1}^{n}f(i)$

$\sum_{i=1}^{n}h(i)=\sum_{i=1}^{n}\sum_{d|i}g(d)\cdot f(\frac{i}{d})\\\to =\sum_{d=1}^{n}g(d)\cdot\sum_{i=1}^{\lfloor\frac{n}{d}\rfloor}f({i})$

$[Math Processing Error]\to \sum_{i=1}^{n}h(i)=\sum_{d=1}^{n}g(d)\cdot S(\lfloor\frac{n}{d}\rfloor)$

接着，我们将右边式子的第一项给提出来，可以得到：

$\sum_{i=1}^{n}h(i)=g(1)\cdot S(n)+\sum_{d=2}^{n}g(d)\cdot S(\lfloor\frac{n}{d}\rfloor)$

$\to g(1)S(n)=\sum_{i=1}^{n}h(i)-\sum_{d=2}^{n}g(d)\cdot S(\lfloor\frac{n}{d}\rfloor) $

其中$h(i)=(f*g)(i)$

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=6e6+50;
unordered_map<int,int>m;
unordered_map<ll,ll>p;
bool vis[maxn];
int mu[maxn],sum_mu[maxn],phi[maxn];
ll sum_phi[maxn];
int cnt,prime[maxn];

void init(int N){
    phi[1]=mu[1]=1;
    for(int i=2;i<=N;i++){
        if(!vis[i]){
            prime[++cnt]=i;
            mu[i]=-1;phi[i]=i-1;
        }
        for(int j=1;j<=cnt;j++){
            if(i*prime[j]>N)break;
            vis[i*prime[j]]=true;
            if(i%prime[j]==0){
                phi[i*prime[j]]=phi[i]*prime[j];
                break;
            }
            mu[i*prime[j]]=-mu[i];
            phi[i*prime[j]]=phi[i]*(prime[j]-1);
        }
    }
    for(int i=1;i<=N;i++){
        sum_mu[i]=sum_mu[i-1]+mu[i];
        sum_phi[i]=sum_phi[i-1]+phi[i];
    }
}
int getmu(int x){
    if(x<=6e6)return sum_mu[x];
    if(m[x])return m[x];
    int ans=1;
    for(int l=2,r;l<=x;l=r+1){
        r=x/(x/l);
        ans-=(r-l+1)*getmu(x/l);
    }
    return m[x]=ans;
}
ll getphi(ll x){
    if(x<=6e6)return sum_phi[x];
    if(p[x])return p[x];
    ll ans=x*(x+1)/2;
    for(ll l=2,r;l<=x;l=r+1){
        r=x/(x/l);
        ans-=(r-l+1)*getphi(x/l);

    }
    return p[x]=ans;
}
int main(){
    int t,n;
    cin>>t;
    init(6e6);
    while(t--){
        cin>>n;
        cout<<getphi(n)<<" "<<getmu(n)<<endl;
    }
    return 0;
}

Lucy筛(素数个数素数和)O(n^4/3)

#include<bits/stdc++.h>

using namespace std;
typedef long long ll;

ll check(ll v, ll n, ll ndr, ll nv) {
    return v >= ndr ? (n / v - 1) : (nv - v);
}

// ll S[10000000];
// ll V[10000000];
ll primenum(ll n) // O(n^(3/4))
{
  ll r = (ll)sqrt(n);
  ll ndr = n / r;
  assert(r*r <= n && (r+1)*(r+1) > n);
  ll nv = r + ndr - 1;
  std::vector<ll> S(nv+1);
  std::vector<ll> V(nv+1);
  for(ll i=0;i<r;i++) {
    V[i] = n / (i+1);
  }
  for(ll i=r;i<nv;i++) {
    V[i] = V[i-1] - 1;
  }
  for(ll i = 0;i<nv;i++) {
    S[i] = V[i] - 1; //求素数个数
  }
  for(ll p=2;p<=r;p++) {
    if(S[nv-p] > S[nv-p+1]) {
      ll sp = S[nv-p+1]; // sum of primes smaller than p
      ll p2 = p*p;
  //    std::cout << "p=" << p << '\n'; // p is prime 
      for(ll i=0;i<nv;i++) {
        if(V[i] >= p2) {
          S[i] -= 1LL  * (S[check(V[i] / p, n, ndr, nv)] - sp);// //求素数个数
        }
        else break;
      }
    }
  }
  return S[0];
}
ll primesum(ll n) // O(n^(3/4))
{
  ll r = (ll)sqrt(n);
  ll ndr = n / r;
  assert(r*r <= n && (r+1)*(r+1) > n);
  ll nv = r + ndr - 1;
  std::vector<ll> S(nv+1);
  std::vector<ll> V(nv+1);
  for(ll i=0;i<r;i++) {
    V[i] = n / (i+1);
  }
  for(ll i=r;i<nv;i++) {
    V[i] = V[i-1] - 1;
  }
  for(ll i = 0;i<nv;i++) {
    S[i] = V[i] * ( V[i] + 1) / 2 - 1; //求素数和
  }
  for(ll p=2;p<=r;p++) { // p is prime 
    if(S[nv-p] > S[nv-p+1]) {
      ll sp = S[nv-p+1]; // sum of primes smaller than p
      ll p2 = p*p; 
      for(ll i=0;i<nv;i++) {
        if(V[i] >= p2) {
        S[i] -= p* (S[check(V[i] / p, n, ndr, nv)] - sp); //求素数和
        }
        else break;
      }
    }
  }
  return S[0];
}
int main(int argc, char const *argv[]) {
//  std::cout << primesum(1e6) << '\n';
  std::cout << primenum(1e10) << '\n';
  std::cout << primesum(2e6) << '\n';
  cerr << "Time elapsed: " << 1.0 * clock() / CLOCKS_PER_SEC << " s.\n";
  return 0;
}

数论

数论函数基础

合数分解

int prime[maxn+1];
void getprime(){
    memset(prime,0,sizeof(prime));
    for(int i=2;i<=maxn;i++){
        if(!prime[i])prime[++prime[0]]=i;
        for(int j=1;j<=prime[0]&&prime[j]<=maxn/i;j++){
            prime[prime[j]*i]=1;
            if(i%prime[j]==0)break;
        }
    }
}
ll factor[100][2];
int fatcnt;
int getfactors(ll x){
    fatcnt=0;
    ll tmp=x;
    for(int i=1;i<=prime[0]&&prime[i]<=tmp/prime[i];i++){
        factor[fatcnt][1]=0;
        if(tmp%prime[i]==0){
            factor[fatcnt][0]=prime[i];
            while(tmp%prime[i]==0){
                factor[fatcnt][1]++;
                tmp/=prime[i];
            }
            fatcnt++;
        }
    }
    if(tmp!=1){
        factor[fatcnt][0]=tmp;
        factor[fatcnt++][1]=1;
    }
    return fatcnt;
}

欧拉函数

欧拉降幂

A^Bmod C=A^(B mod phji(C)) %C gcd(a,c)==1

A^B mod C=A^B %C (B<phi(C))

A^B mod C=A^(B mod phi(C)+phi(C))%C (B>=phi(C))

得出单个数的欧拉函数 O(sqrt n)

ll euler(ll n)
{
    ll rt = n;
    for (int i = 2; i * i <= n; i++)
        if (n % i == 0)
        {
            rt -= rt / i;
            while (n % i == 0) n /= i;
        }
    if (n > 1) rt -= rt / n;
    return rt;
}

筛法欧拉函数

const int N = "Edit";
int phi[N] = {0, 1};
void caleuler()
{
    for (int i = 2; i < N; i++)
        if (!phi[i])
            for (int j = i; j < N; j += i)
            {
                if (!phi[j]) phi[j] = j;
                phi[j] = phi[j] / i * (i - 1);
            }
}

线性筛

bool check[maxn];
int phi[maxn];
int prime[maxn];
int tot;
void phi_and_prime_table(int N){
    memset(check,false,sizeof(check));
    phi[1]=1;
    tot=0;
    for(int i=2;i<=N;i++){
        if(!check[i]){
            prime[tot++]=i;
            phi[i]=i-1;
        }
        for(int j=0;j<tot;j++){
            if(i*prime[j]>N)break;
            check[i*prime[j]]=true;
            if(i%prime[j]==0){
                phi[i*prime[j]]=phi[i]*prime[j];
                break;
            }
            else{
                phi[i*prime[j]]=phi[i]*(prime[j]-1);
            }
        }
    }
}

莫比乌斯

莫比乌斯函数

int prime[maxn];
bool notprime[maxn];
int mu[maxn];
void getMobius(int N){
    mu[1]=1;    ///μ函数的1是特殊情况
    int tot=0;
    for(int i=2;i<=N;i++){
        if(!notprime[i]){
            prime[++tot]=i;
            mu[i]=-1;
        }
        for(int j=1;j<=tot;j++){
            if(i*prime[j]>N)break;
            notprime[i*prime[j]]=true;
            if(i%prime[j]==0){
                mu[i*prime[j]]=0;   ///i中已经包括了prime[j]
                break;
            }
            else{
                mu[i*prime[j]]=-mu[i];
            }
        }
    }
}

模线性方程

二次剩余

LL w;
struct Point{//x + y*sqrt(w)
    LL x;
    LL y;
};
LL mod(LL a, LL p){
    a %= p;
    if (a < 0){
        a += p;
    }
    return a;
}
Point point_mul(Point a, Point b, LL p){
    Point res;
    res.x = mod(a.x * b.x, p);
    res.x += mod(w * mod(a.y * b.y, p), p);
    res.x = mod(res.x, p);
    res.y = mod(a.x * b.y, p);
    res.y += mod(a.y * b.x, p);
    res.y = mod(res.y , p);
    return res;
}

Point power(Point a, LL b, LL p){
    Point res;
    res.x = 1;
    res.y = 0;
    while(b){
        if (b & 1){
            res = point_mul(res, a, p);
        }
        a = point_mul(a, a, p);
        b = b >> 1;
    }
    return res;
}

LL quick_power(LL a, LL b, LL p){//(a^b)%p
    LL res = 1;
    while(b){
        if (b & 1){
            res = (res * a) % p;
        }
        a = (a * a) % p;
        b = b >> 1;
    }
    return res;
}
LL Legendre(LL a, LL p){ // a^((p-1)/2)
    return quick_power(a, (p - 1) >> 1, p);
}

LL equation_solve(LL b, LL p){//求解x^2=b(%p)方程解
    if (b == 0)
        return 0;
    if ((Legendre(b, p) + 1) % p == 0){
        return -1;//表示没有解
    }
    LL a, t;
    while(true){
        a = rand() % p;
        t = a * a - b;
        t = mod(t, p);
        if ((Legendre(t, p) + 1) % p == 0){
            break;
        }
    }
    w = t;
    Point temp, res;
    temp.x = a;
    temp.y = 1;
    res = power(temp, (p + 1) >> 1, p);
    return res.x;
}

中国剩余定理

///要求m 两两互质 X=ri(mod mi) 引用返回通解 X=re+k*mo
void crt(ll r[],ll m[],ll n,ll &re,ll &mo){
    mo=1,re=0;
    for(int i=0;i<n;i++)mo*=m[i];
    for(int i=0;i<n;i++){
        ll x,y,tm=mo/m[i];
        ll d=exgcd(tm,m[i],x,y);
        re=(re+tm*x*r[i])%mo;
    }
    re=(re+mo)%mo;
}

ExCRT

//mi可以不两两互质
bool excrt(ll r[], ll m[], ll n, ll &re, ll &mo)
{
    ll x, y;
    mo = m[0], re = r[0];
    for (int i = 1; i < n; i++)
    {
        ll d = exgcd(mo, m[i],  x, y);
        if ((r[i] - re) % d != 0) return 0;
        x = (r[i] - re) / d * x % (m[i] / d);
        re += x * mo;
        mo = mo / d * m[i];
        re %= mo;
    }
    re = (re + mo) % mo;
    return 1;
}

大步小步算法 a^x=b(mod n)

// 求解模方程a^x=b(mod n)。n 为素数。无解返回-1
int log_mod(int a, int b) {
  int m, v, e = 1, i;
  m = (int)sqrt(MOD);
  v = inv(pow_mod(a, m));
  map <int,int> x;
  x[1] = 0;
  for(i = 1; i < m; i++){ e = mul_mod(e, a); if (!x.count(e)) x[e] = i; }
  for(i = 0; i < m; i++){
    if(x.count(b)) return i*m + x[b];
    b = mul_mod(b, v);
  }
  return -1;
}

扩展大步小步(gcd!=1)

int ex_BSGS(int A,int B,int C)
{
    if(B==1) return 0;
    int k=0,tmp=1,d;
    while(1)
    {
        d=__gcd(A,C);
        if(d==1) break;
        if(B%d) return -1;
        B/=d; C/=d;
        tmp=1LL*tmp*(A/d)%C;
        k++;
        if(tmp==B) return k;
    }
    map<int,int>mp;
    mp.clear();
    int mul=B;
    mp[B]=0;
    int m=ceil(sqrt(1.0*C));
    for(int j=1;j<=m;++j)
    {
        mul=1LL*mul*A%C;
        mp[mul]=j;
    }
    int am=fastpow(A,m,C);
    mul=tmp;
    for(int j=1;j<=m;++j)
    {
        mul=1LL*mul*am%C;
        if(mp.count(mul)) return j*m-mp[mul]+k;
    }
    return -1;
}

线性基

struct Linear_Basis{
	long long d[65],p[65];
	int cnt;
	Linear_Basis(){
		memset(d,0,sizeof(d));
		memset(p,0,sizeof(p));
		cnt=0;
	}

	bool ins(long long val){
		for (int i=62;i>=0;i--) {
			if (val&(1LL<<i)){
				if (!d[i]){
					d[i]=val;
					break;
				}
				val^=d[i];
			}
		}
		return val>0;
	}

	long long query_max(long long D=0LL){
		long long ret=D;
		for (int i=62;i>=0;i--)
			if ((ret^d[i])>ret) ret^=d[i];
		return ret;
	}

    long long query_min(long long D=0LL){
        long long ret=D;
        for(int i=0;i<=62;i++){
            if(d[i]) ret^=d[i];
        }
        return ret;
    }

	void rebuild(){
		for (int i=1;i<=62;i++)
			for (int j=0;j<i;j++)
				if (d[i]&(1LL<<j)) d[i]^=d[j];
		cnt=0;
		for (int i=0;i<=62;i++)
			if (d[i]) p[cnt++]=d[i];
	}
    //第K大
	long long kthquery(long long k){
		long long ret=0;
		if (k>=(1LL<<cnt)) return -1;
		for (int i=0;i<=62;i++)
			if (k&(1LL<<i)) ret^=p[i];
		return ret;
	}
	Linear_Basis merge(const Linear_Basis &n1,const Linear_Basis &n2){
	    Linear_Basis ret=n1;
	    for(int i=62;i>=0;i--)
            if(n2.d[i])ret.ins(n2.d[i]);
        return ret;
	}
};
struct node{
    int base[32];
    node(){for(int i=0;i<32;i++)base[i]=0;}
    void insert(int x){
        for(int i=31;~i;i--){
            if(x>>i&1){
                if(!base[i]){
                    base[i]=x;
                    return;
                }
                x^=base[i];
            }
        }
    }
    int check(int x) {
        for (int i = 31; ~i; i--)
        if (x >> i & 1) {
            if (!base[i]) {
                return 0;
            }
            x ^= base[i];
        }
        return 1;
    }
    node intersect(node a, node b) {///线性基求交
        node tmp, d, ans;
        for (int i = 0; i < 32; i++)
        if (a.base[i]) {
            tmp.base[i] = a.base[i];
            d.base[i] = 1 << i;
        }
        for (int i = 31; ~i; i--)
        if (b.base[i]) {
            int flag = 1, k = 0, v = b.base[i];
            for (int j = i; ~j; j--)
            if (v >> j & 1) {
                if (tmp.base[j]) {
                    v ^= tmp.base[j];
                    k ^= d.base[j];
                }
                else {
                    flag = 0;
                    tmp.base[j] = v;
                    d.base[j] = k;
                    break;
                }
            }
            if (flag) {
                int val = 0;
                for (int j = 31; ~j; j--)
                if (k >> j & 1)
                    val ^= a.base[j];
                ans.insert(val);
            }
        }
        return ans;
    }
}tree[maxn<<2];

几何

知识点

1	线段上的整点个数，(x1,y1)(x2,y2)两点连线之间的整点数是gcd(\|x1−x2\|,\|y1−y2\|)+1

弧度转换,点绕点旋转

欧拉定理：设平面图的顶点数，边数和面数分别为V,E,和F，则V+F-E=2

其中顺时针旋转为负，逆时针旋转为正，角度angle是弧度值，如旋转30度转换为弧度为： $angle = pi/180 * 30$。

4、度与角度的转换
根据圆为$360 º$，弧度为$2π$，即 $360º = 2π$

4.1 角度转弧度：$2π / 360 = π / 180 ≈ 0.0174rad$, 即: $度数 (π / 180） = 弧度$
例如：将30º转为弧度rad
$ 30º (π / 180）= 0.523320 rad $

4.2 弧度转角度: $360 / 2π = 180 / π ≈ 57.3º$, 即: $ 弧度 (180 / π） = 度数$
例如：将$0.523320rad$转为度º
$0.523320rad (180 / π) = 29.9992352688º $

若o不是原点，则可先将a点坐标转换为相对坐标计算，计算结果再加上o点坐标。

参与计算的a点坐标实际应为 a - 0,最终计算公式如下：

$b.x = ( a.x - o.x)cos(angle) - (a.y - o.y)sin(angle) + o.x$

$b.y = (a.x - o.x)sin(angle) + (a.y - o.y)cos(angle) + o.y$

刘汝佳套餐

Point

const double inf=1e200;
const double eps=1e-8;
const double pi=4*atan(1.0);
struct Point{
    double x,y;
    Point(double a=0,double b=0):x(a),y(b){}
    void input(){
        cin>>x>>y;
    }
};

typedef Point Vector;
int dcmp(double x){ return fabs(x)<eps?0:(x<0?-1:1);}
//向量+向量=向量，点+向量=点
Vector operator +(Vector A,Vector B){ return Vector(A.x+B.x,A.y+B.y);}
//点-点=向量
Vector operator -(Point A,Point B){ return Vector(A.x-B.x,A.y-B.y);}
//向量*数=向量
Vector operator *(Vector A,double p){ return Vector(A.x*p,A.y*p);}
//向量/数=向量
Vector operator /(Vector A,double p){ return Vector(A.x/p,A.y/p);}

bool operator<(const Point& a, const Point& b){
    return a.x < b.x || (a.x == b.x && a.y < b.y);
}
bool operator ==(const Point& a,const Point& b) {
    return dcmp(a.x-b.x)==0&&dcmp(a.y-b.y)==0;
}
double dot(Vector A,Vector B){ return A.x*B.x+A.y*B.y;}
double det(Vector A,Vector B){ return A.x*B.y-A.y*B.x;}
double dot(Point O,Point A,Point B){ return dot(A-O,B-O);}
double det(Point O,Point A,Point B){ return det(A-O,B-O);}
double length(Vector A){ return sqrt(dot(A,A));}
double angle(Vector A,Vector B){ return acos(dot(A,B)/length(A)/length(B));}
double area2(Point A,Point B,Point C){return det(B-A,C-A);}

//rad是弧度
Vector Rotate(Vector A,double rad)
{
    return Vector(A.x*cos(rad)-A.y*sin(rad),
                  A.x*sin(rad)+A.y*cos(rad));
}
//调用前请确保A不是零向量 单位法向量 左转90°长度归一
Vector normal(Vector A)
{
    double L = length(A);
    return Vector(-A.y / L, A.x / L);
}
//调用前保证两条直线P+tv和Q+tw有唯一交点。当且仅当Cross(v, w)非0->平行
Point jiaoPoint(Point p,Vector v,Point q,Vector w)
{   //p+tv q+tw，点加向量表示直线，求直线交点
    Vector u=p-q;
    double t=det(w,u)/det(v,w);
    return p+v*t;
}

double distoline(Point P,Point A,Point B)
{
    //点到直线距离
    Vector v1=B-A,v2=P-A;
    return fabs(det(v1,v2)/length(v1));//如果不取绝对值，得到的是有向距离
}
double distoseg(Point P,Point A,Point B)
{
    //点到线段距离 ///钝角<0,锐角>0,直角=0
    if(A==B) return length(P-A);
    Vector v1=B-A,v2=P-A,v3=P-B;
    if(dcmp(dot(v1,v2))<0) return length(v2);
    else if(dcmp(dot(v1,v3))>0) return length(v3);
    return fabs(det(v1,v2)/length(v1));
}
Point GetLineProjection(Point p,Point A,Point B){
    //点P到AB的投影
    Vector v=B - A;
    return A + v * (dot(v,p-A)/dot(v,v));
}
bool SegmentProperIntersection(Point a1,Point a2,Point b1,Point b2)   {
    //规范相交
    double c1=det(a2-a1,b1-a1),c2=det(a2-a1,b2-a1);
    double c3=det(b2-b1,a1-b1),c4=det(b2-b1,a2-b1);
    return dcmp(c1)*dcmp(c2)<0&&dcmp(c3)*dcmp(c4)<0; ///端点相交加上等于
    /*
    &&max(a1.x,a2.x)>=min(b1.x,b2.x)
    &&max(b1.x,b2.x)>=min(a1.x,a2.x)
    &&max(a1.y,a2.y)>=min(b1.y,b2.y)
    &&max(b1.y,b2.y)>=min(a1.y,a2.y);
    */
}
bool isPointOnSegment(Point p,Point a1,Point a2)
{
    //点是否在线段上
    return dcmp(det(a1-p,a2-p)==0)&&dcmp(dot(a1-p,a2-p)<0);
}

Circle


struct Line
{
    Point p;    //直线上任意一点
    Vector v;   //方向向量。它的左边就是对应的半平面
    double ang; //极角。即从x正半轴旋转到向量v所需要的角（弧度）
    Line() {}
    Line(Point p, Vector v) : p(p), v(v) { ang = atan2(v.y, v.x); }
    bool operator<(const Line& L) const // 排序用的比较运算符
    {
        return ang < L.ang;
    }
    Point point(double t) { return p + v * t; }
};

struct Circle
{
    Point c;
    double r;
    Circle(Point c=Point(0,0), double r=0) : c(c), r(r) {}
    Point point(double a) { return Point(c.x + cos(a) * r, c.y + sin(a) * r); }
};

int getLineCircleIntersection(Line L, Circle C, double& t1, double& t2, vector<Point>& sol)
{
    double a = L.v.x, b = L.p.x - C.c.x, c = L.v.y, d = L.p.y - C.c.y;
    double e = a * a + c * c, f = 2 * (a * b + c * d), g = b * b + d * d - C.r * C.r;
    double delta = f * f - 4 * e * g; //判别式
    if (dcmp(delta) < 0) return 0;    //相离
    if (dcmp(delta) == 0)             //相切
    {
        t1 = t2 = -f / (2 * e);
        sol.push_back(L.point(t1));
        return 1;
    }
    //相交
    t1 = (-f - sqrt(delta)) / (2 * e);
    t2 = (-f + sqrt(delta)) / (2 * e);
    sol.push_back(L.point(t1));
    sol.push_back(L.point(t2));
    return 2;
}

double angle(Vector v) { return atan2(v.y, v.x); }

int getCircleCircleIntersection(Circle C1, Circle C2, vector<Point>& sol)
{
    double d = Length(C1.c - C2.c);
    if (dcmp(d) == 0)
    {
        if (dcmp(C1.r - C2.r) == 0) return -1; //两圆重合
        return 0;
    }
    if (dcmp(C1.r + C2.r - d) < 0) return 0;       //内含
    if (dcmp(fabs(C1.r - C2.r) - d) > 0) return 0; //外离

    double a = angle(C2.c - C1.c); //向量C1C2的极角
    double da = acos((C1.r * C1.r + d * d - C2.r * C2.r) / (2 * C1.r * d));
    //C1C2到C1P1的角
    Point p1 = C1.point(a - da), p2 = C1.point(a + da);
    sol.push_back(p1);
    if (p1 == p2) return 1;
    sol.push_back(p2);
    return 2;
}
//过点p到圆C的切线，v[i]是第i条切线的向量，返回切线条数
int getTangents(Point p, Circle C, Vector* v)
{
    Vector u = C.c - p;
    double dist = Length(u);
    if (dist < C.r)
        return 0;
    else if (dcmp(dist - C.r) == 0)
    { //p在圆上，只有一条切线
        v[0] = Rotate(u, pi / 2);
        return 1;
    }
    else
    {
        double ang = asin(C.r / dist);
        v[0] = Rotate(u, -ang);
        v[1] = Rotate(u, +ang);
        return 2;
    }
}

//两圆的公切线
//返回切线的条数。-1表示无穷条切线。
//a[i]和b[i]分别是第i条切线在圆A和圆B上的切点
int getTangents(Circle A, Circle B, Point* a, Point* b)
{
    int cnt = 0;
    if (A.r < B.r)
    {
        swap(A, B);
        swap(a, b);
    }
    int d2 = (A.c.x - B.c.x) * (A.c.x - B.c.x) + (A.c.y - B.c.y) * (A.c.y - B.c.y);
    int rdiff = A.r - B.r;
    int rsum = A.r + B.r;
    if (d2 < rdiff * rdiff) return 0; //内含
    double base = atan2(B.c.y - A.c.y, B.c.x - A.c.x);
    if (d2 == 0 && A.r == B.r) return -1; //无限多条切线
    if (d2 == rdiff * rdiff)
    { //内切，一条切线
        a[cnt] = A.point(base);
        b[cnt] = B.point(base);
        cnt++;
        return 1;
    }
    //有外共切线
    double ang = acos((A.r - B.r) / sqrt(d2));
    a[cnt] = A.point(base + ang);
    b[cnt] = B.point(base + ang);
    cnt++;
    a[cnt] = A.point(base + ang);
    b[cnt] = B.point(base - ang);
    cnt++;
    if (d2 == rsum * rsum)
    {
        a[cnt] = A.point(base);
        b[cnt] = B.point(pi + base);
        cnt++;
    }
    else if (d2 > rsum * rsum)
    {
        double ang = acos((A.r + B.r) / sqrt(d2));
        a[cnt] = A.point(base + ang);
        b[cnt] = B.point(pi + base + ang);
        cnt++;
        a[cnt] = A.point(base - ang);
        b[cnt] = B.point(pi + base - ang);
        cnt++;
    }
    return cnt;
}
//三角形外接圆（三点保证不共线）
Circle CircumscribedCircle(Point p1, Point p2, Point p3)
{
    double Bx = p2.x - p1.x, By = p2.y - p1.y;
    double Cx = p3.x - p1.x, Cy = p3.y - p1.y;
    double D = 2 * (Bx * Cy - By * Cx);
    double cx = (Cy * (Bx * Bx + By * By) - By * (Cx * Cx + Cy * Cy)) / D + p1.x;
    double cy = (Bx * (Cx * Cx + Cy * Cy) - Cx * (Bx * Bx + By * By)) / D + p1.y;
    Point p = Point(cx, cy);
    return Circle(p, Length(p1 - p));
}

//三角形内切圆
Circle InscribedCircle(Point p1, Point p2, Point p3)
{
    double a = Length(p2 - p3);
    double b = Length(p3 - p1);
    double c = Length(p1 - p2);
    Point p = (p1 * a + p2 * b + p3 * c) / (a + b + c);
    return Circle(p, distoline(p, p1, p2));
}
double ok(double x){
    while(x>=pi)x-=pi;
    while(x<0)x+=pi;
    return x;
}

//平行线.
void Parallel(Point A,Point B,double r,vector<Line> &sol){
    Vector AB=normal(B-A);
    AB=AB*r;
    Point AA=A+AB,BB=B+AB;
    Line L1=Line(AA,BB-AA);
    sol.push_back(L1);
    AA=A-AB,BB=B-AB;
    Line L2=Line(AA,BB-AA);
    sol.push_back(L2);
}
double torad(double deg){
    return deg/180*pi;
}

Polygon


typedef vector<Point> Polygon;
//多边形的有向面积
double PolygonArea(Polygon po)
{
    int n = po.size();
    double area = 0.0;
    for (int i = 1; i < n - 1; i++)
        area += det(po[i] - po[0], po[i + 1] - po[0]);
    return area / 2;
}

int isPointInPolygon(Point p,vector<Point>poly)
{
    //判断点与多边形的位置关系
    int wn=0,sz=poly.size();
    for(int i=0;i<sz;i++){
        if(isPointOnSegment(p,poly[i],poly[(i+1)%sz])) return -1; //边界上
        int k=dcmp(det(poly[(i+1)%sz]-poly[i],p-poly[i]));
        int d1=dcmp(poly[i].y-p.y);
        int d2=dcmp(poly[(i+1)%sz].y-p.y);
        if(k>0&&d1<=0&&d2>0) wn++;
        if(k<0&&d2<=0&&d1>0) wn--;
    }
    if(wn!=0) return 1;//内部
    return 0;          //外部
}
//凸包(Andrew算法)
//如果不希望在凸包的边上有输入点，把两个 <= 改成 <
//如果不介意点集被修改，可以改成传递引用
Polygon ConvexHull(vector<Point> p){
    sort(p.begin(),p.end());
    p.erase(unique(p.begin(),p.end()),p.end());
    int n=p.size(),m=0;
    Polygon res(n+1);
    for(int i=0;i<n;i++){
        while(m>1&&det(res[m-1]-res[m-2],p[i]-res[m-2])<=0)m--;
        res[m++]=p[i];
    }
    int k=m;
    for(int i=n-2;i>=0;i--){
        while(m>k&&det(res[m-1]-res[m-2],p[i]-res[m-2])<=0)m--;
        res[m++]=p[i];
    }
    m-=n>1;
    res.resize(m);
    return res;
}

付队模板

#define mp make_pair
typedef long long ll;
const double inf=1e200;
const double eps=1e-8;
const double pi=4*atan(1.0);
struct point{
    double x,y;
    point(double a=0,double b=0):x(a),y(b){}
};
int dcmp(double x){ return fabs(x)<eps?0:(x<0?-1:1);}
point operator +(point A,point B) { return point(A.x+B.x,A.y+B.y);}
point operator -(point A,point B) { return point(A.x-B.x,A.y-B.y);}
point operator *(point A,double p){ return point(A.x*p,A.y*p);}
point operator /(point A,double p){ return point(A.x/p,A.y/p);}
point rotate(point A,double rad){
    return point(A.x*cos(rad)-A.y*sin(rad), A.x*sin(rad)+A.y*cos(rad));
}
bool operator ==(const point& a,const point& b) {
     return dcmp(a.x-b.x)==0&&dcmp(a.y-b.y)==0;
}
double dot(point A,point B){ return A.x*B.x+A.y*B.y;}
double det(point A,point B){ return A.x*B.y-A.y*B.x;}
double dot(point O,point A,point B){ return dot(A-O,B-O);}
double det(point O,point A,point B){ return det(A-O,B-O);}
double length(point A){ return sqrt(dot(A,A));}
double angle(point A,point B){ return acos(dot(A,B)/length(A)/length(B));}
double distoline(point P,point A,point B)
{
    //点到直线距离
    point v1=B-A,v2=P-A;
    return fabs(det(v1,v2)/length(v1));
}
double distoseg(point P,point A,point B)
{
    //点到线段距离
    if(A==B) return length(P-A);
    point v1=B-A,v2=P-A,v3=P-B;
    if(dcmp(dot(v1,v2))<0) return length(v2);
    else if(dcmp(dot(v1,v3))>0) return length(v3);
    return fabs(det(v1,v2)/length(v1));
}
double Ployarea(vector<point>p)
{
    //多边形面积
    double ans=0; int sz=p.size();
    for(int i=1;i<sz-1;i++) ans+=det(p[i]-p[0],p[i+1]-p[0]);
    return ans/2.0;
}
bool SegmentProperIntersection(point a1,point a2,point b1,point b2)   {
    //规范相交
    double c1=det(a2-a1,b1-a1),c2=det(a2-a1,b2-a1);
    double c3=det(b2-b1,a1-b1),c4=det(b2-b1,a2-b1);
    return dcmp(c1)*dcmp(c2)<0&&dcmp(c3)*dcmp(c4)<0;
}
bool isPointOnSegment(point p,point a1,point a2)
{
    //点是否在线段上
    return dcmp(det(a1-p,a2-p)==0&&dcmp(dot(a1-p,a2-p))<0);
}
int isPointInPolygon(point p,vector<point>poly)
{
    //判断点与多边形的位置关系
    int wn=0,sz=poly.size();
    for(int i=0;i<sz;i++){
        //在边上
        if(isPointOnSegment(p,poly[i],poly[(i+1)%sz])) return -1;
        int k=dcmp(det(poly[(i+1)%sz]-poly[i],p-poly[i]));
        int d1=dcmp(poly[i].y-p.y); int d2=dcmp(poly[(i+1)%sz].y-p.y);
        if(k>0&&d1<=0&&d2>0) wn++;
        if(k<0&&d2<=0&&d1>0) wn--;
    }
    if(wn!=0) return 1;//内部
    return 0;          //外部
}
double seg(point O,point A,point B){
    if(dcmp(B.x-A.x)==0) return (O.y-A.y)/(B.y-A.y);
    return (O.x-A.x)/(B.x-A.x);
}
pair<double,int>s[110*60];
double polyunion(vector<point>*p,int N){ //有多个才加*,单个不加，有改变的加&
    //求多边形面积并
    double res=0;
    for(int i=0;i<N;i++){
        int sz=p[i].size();
        for(int j=0;j<sz;j++){
            int m=0;
            s[++m]=mp(0,0);
            s[++m]=mp(1,0);
            point a=p[i][j],b=p[i][(j+1)%sz];
            for(int k=0;k<N;k++){
                if(i!=k){
                    int sz2=p[k].size();
                    for(int ii=0;ii<sz2;ii++){
                        point c=p[k][ii],d=p[k][(ii+1)%sz2];
                        int c1=dcmp(det(b-a,c-a));
                        int c2=dcmp(det(b-a,d-a));
                        if(c1==0&&c2==0){
                            if(dcmp(dot(b-a,d-c))){
                                s[++m]=mp(seg(c,a,b),1);
                                s[++m]=mp(seg(c,a,b),-1);
                            }
                        }
                        else{
                            double s1=det(d-c,a-c);
                            double s2=det(d-c,b-c);
                            if(c1>=0&&c2<0) s[++m]=mp(s1/(s1-s2),1);
                            else if(c1<0&&c2>=0) s[++m]=mp(s1/(s1-s2),-1);
                        }
                    }
                }
            }
            sort(s+1,s+m+1);
            double pre=min(max(s[1].first,0.0),1.0),now,sum=0;
            int cov=s[0].second;
            for(int j=2;j<=m;j++){
                now=min(max(s[j].first,0.0),1.0);
                if(!cov) sum+=now-pre;
                cov+=s[j].second;
                pre=now;
            }
            res+=det(a,b)*sum;
        }
    }
    return -(res/2);
}
point jiaopoint(point p,point v,point q,point w)
{   //p+tv q+tw，点加向量表示直线，求直线交点
    point u=p-q;
    double t=det(w,u)/det(v,w);
    return p+v*t;
}
point GetCirPoint(point a,point b,point c)
{
    point p=(a+b)/2;    //ad中点
    point q=(a+c)/2;    //ac中点
    point v=rotate(b-a,pi/2.0),w=rotate(c-a,pi/2.0);   //中垂线的方向向量
    if (dcmp(length(det(v,w)))==0)    //平行
    {
        if(dcmp(length(a-b)+length(b-c)-length(a-c))==0) return (a+c)/2;
        if(dcmp(length(b-a)+length(a-c)-length(b-c))==0) return (b+c)/2;
        if(dcmp(length(a-c)+length(c-b)-length(a-b))==0) return (a+b)/2;
    }
    return jiaopoint(p,v,q,w);
}
point MinCircular(point *P,int n)
{
    //最小圆覆盖 ,看起来是O(N^3)，期望复杂度为O(N)
    random_shuffle(P+1,P+n+1);    //随机化
    point c=P[1]; double r=0;   //c 圆心,,//r 半径
    for (int i=2;i<=n;i++)
        if (dcmp(length(c-P[i])-r)>0)    //不在圆内
        {
            c=P[i],r=0;
            for (int j=1;j<i;j++)
                if (dcmp(length(c-P[j])-r)>0)
                {
                    c=(P[i]+P[j])/2.0;
                    r=length(c-P[i]);
                    for (int k=1;k<j;k++)
                        if (dcmp(length(c-P[k])-r)>0)
                        {
                            c=GetCirPoint(P[i],P[j],P[k]);
                            r=length(c-P[i]);
                        }
                }
        }
    //cout<<r<<":"<<c.x<<" "<<c.y<<endl;
    return c;
}
const int maxn=400010;
bool cmp(point a,point b){ return a.x==b.x?a.y<b.y:a.x<b.x; }
point f[maxn],c[maxn],ch[maxn];
void convexhull(point *a,int n,int &top)
{
    //水平序的Andrew算法求凸包。
    sort(a+1,a+n+1,cmp); top=0;
    for(int i=1;i<=n;i++){ //求下凸包
        while(top>=2&&det(ch[top-1],ch[top],a[i])<=0) top--;
        ch[++top]=a[i];
    }
    int ttop=top;
    for(int i=n-1;i>=1;i--){ //求上凸包
        while(top>ttop&&det(ch[top-1],ch[top],a[i])<=0) top--;
        ch[++top]=a[i];
    }
}
void P(double x)
{
    //if(fabs(x)<0.000001) puts("0.00000000"); else
    printf("%.9lf",x);
}

球体积交

#include <bits/stdc++.h>
using namespace std;
 
const int maxn = 1e2 + 5;
const double pi = acos(-1.0);
const double eps = 1e-8;
 
int Sgn(double X) {
    if (fabs(X) < eps) {
        return 0;
    }
    return X < 0 ? -1 : 1;
}
 
struct Point {
    double X, Y, Z;
 
    void Input() {
        scanf("%lf%lf%lf", &X, &Y, &Z);
    }
};
 
typedef Point Vector;
 
Vector operator + (Vector Key1, Vector Key2) {
    return (Vector){Key1.X + Key2.X, Key1.Y + Key2.Y, Key1.Z + Key2.Z};
}
 
Vector operator - (Vector Key1, Vector Key2) {
    return (Vector){Key1.X - Key2.X, Key1.Y - Key2.Y, Key1.Z - Key2.Z};
}
 
double operator * (Vector Key1, Vector Key2) {
    return Key1.X * Key2.X + Key1.Y * Key2.Y + Key1.Z * Key2.Z;
}
 
double Length(Vector Key) {
    return sqrt(Key * Key);
}
 
double operator ^ (Vector Key1, Vector Key2) {
    return Length((Vector){Key1.Y * Key2.Z - Key1.Z * Key2.Y, Key1.Z * Key2.X - Key1.X * Key2.Z, Key1.X * Key2.Y - Key1.Y * Key2.X});
}
 
double DisPointToPoint(Point Key1, Point Key2) {
    return sqrt((Key1 - Key2) * (Key1 - Key2));
}
 
struct Sphere {
    double pi=acos(-1.0);
    Point Center;
    double Radius;
 
    void Input() {
        Center.Input();
        scanf("%lf", &Radius);
    }
    double get(){
        return (4.0/3.0)*pi*Radius*Radius*Radius;
    }
};
 
double CalVolume(Sphere Key) {
    return 4.0 / 3.0 * pi * Key.Radius * Key.Radius * Key.Radius;
}
 
double SphereIntersectVolume(Sphere Key1, Sphere Key2) {
    double Ans = 0.0;
    double Dis = DisPointToPoint(Key1.Center, Key2.Center);
    if (Sgn(Dis - Key1.Radius - Key2.Radius) >= 0) {
        return Ans;
    }
    if (Sgn(Key2.Radius - (Dis + Key1.Radius)) >= 0) {
        return CalVolume(Key1);
    }
    else if (Sgn(Key1.Radius - (Dis + Key2.Radius)) >= 0) {
        return CalVolume(Key2);
    }
    double Length1 = ((Key1.Radius * Key1.Radius - Key2.Radius * Key2.Radius) / Dis + Dis) / 2;
    double Length2 = Dis - Length1;
    double X1 = Key1.Radius - Length1, X2 = Key2.Radius - Length2;
    double V1 = pi * X1 * X1 * (Key1.Radius - X1 / 3.0);
    double V2 = pi * X2 * X2 * (Key2.Radius - X2 / 3.0);
    return V1 + V2;
}
 
int T;
int N;
Sphere a;
Sphere b;
double ans;
 
int main(int argc, char *argv[]) {
 
    a.Input();
    b.Input();
    ans=a.get()+b.get()-SphereIntersectVolume(a,b);
    cout<<fixed<<setprecision(15);
    cout<<ans<<endl;
    return 0;
}

其他

分块

    int n;
    cin>>n;
    block=sqrt(n);
    for(int i=1;i<=n;i++){
        in[i]=(i-1)/block+1;
        cin>>a[i];
        s[in[i]]+=a[i];
    }
ll query(int l,int r){
    ll ans=0;
    if(in[l]==in[r]){
        for(int i=l;i<=r;i++)ans+=a[i];
        return ans;
    }
    for(int i=l;in[i]==in[l];i++)ans+=a[i];
    for(int i=r;in[i]==in[r];i--)ans+=a[i];
    for(int i=in[l]+1;i<in[r];i++)ans+=(s[i]);
    return ans;
}
block*(i-1)+1 ///块i的第一个位置
///查询区间小于一个数的个数   二分
///查询区间某数前驱， 		二分
///在某个位置插入一个数（vector 暴力插入 后定期重构（块大小大于原块的五倍。
v[i].insert( v[i].begin() + wh - 1, x );//插入~ ///在这个块的第wh个位置插入值为x的数。

分块的一些技巧

查询区间一个数的个数（二分

查询区间某数前驱（二分

在某个位置插入一个数（vector 暴力插入后定期重构（块大小大于原块的五倍。

bitset

对于一个叫做bit的bitset：
bit.size()       返回大小（位数）
bit.count()     返回1的个数
bit.any()       返回是否有1
bit.none()      返回是否没有1
bit.set()       全都变成1
bit.set(p)      将第p + 1位变成1（bitset是从第0位开始的！） 
bit.set(p, x)   将第p + 1位变成x
bit.reset()     全都变成0
bit.reset(p)    将第p + 1位变成0
bit.flip()      全都取反
bit.flip(p)     将第p + 1位取反
bit.to_ulong()  返回它转换为unsigned long的结果，如果超出范围则报错
bit.to_ullong() 返回它转换为unsigned long long的结果，如果超出范围则报错
bit.to_string() 返回它转换为string的结果

斜率DP

画图判断交点的位置决定是否剔除

$dp[i][j]=dp[k][j-1]+(sum[i]-sum[k])-h[k+1]*(w[i]-w[k])$

const int maxn=5500+50;

int n,k;
struct node{
    ll h,w;
    bool operator< (const node &o)const{
        return h<o.h;
    }
}my[maxn];
ll dp[5050][5050]; ///前i个木块 做J个

int q[maxn];
int head,tail;
__int128 sum[maxn];
__int128 h[maxn];
__int128 w[maxn];
__int128 getDP(int i,int k,int id){  ///dp[i][id]= dp[i][k]+sum[k+1][i];
    return dp[k][id-1]+(sum[i]-sum[k])-__int128(h[k+1]*(w[i]-w[k]));
}
__int128 getUP(int y,int x,int id){ /// y<x 且x更优秀
    return dp[x][id-1]-dp[y][id-1]+sum[y]-sum[x]-__int128(h[y+1]*w[y])+__int128(h[x+1]*w[x]);
}
__int128 getDOWN(int y,int x,int i){
    return h[x+1]-h[y+1];
}

int main()
{
    std::ios::sync_with_stdio(false);
    cin>>n>>k;
    for(int i=1;i<=n;i++)cin>>my[i].w>>my[i].h;
    sort(my+1,my+1+n);
    for(int i=1;i<=n;i++){
        w[i]=w[i-1]+my[i].w;
        sum[i]=sum[i-1]+1LL*my[i].w*my[i].h;
        h[i]=my[i].h;
    }
    for(int i=1;i<=n;i++)dp[i][1]=sum[i]-sum[0]-h[1]*(w[i]-w[0]);

    for(int j=2;j<=k;j++){
        head=tail=0;
        q[++tail]=j-1;
        for(int i=j;i<=n;i++){
            while(head+2<=tail&&getUP(q[head+1],q[head+2],j)<=getDOWN(q[head+1],q[head+2],j)*w[i])
                head++;
            dp[i][j]=getDP(i,q[head+1],j);
            while(head+2<=tail&&__int128(getUP(q[tail-1],q[tail],j)*getDOWN(i,q[tail],j))<=__int128(getUP(i,q[tail],j)*getDOWN(q[tail-1],q[tail],j)))
     // 取min用<= 取max 用>=
                
     //根据x是递增还是递减 加上取min还是取max 决定大于小于
                
      //min + 递增 下凸包 <=
      //min + 递减 上凸包 >=
      //max + 递增 上凸包 >=
      //max + 递减 下凸包 <=
                tail--;
            q[++tail]=i;
        }
    }
    cout<<dp[n][k]<<endl;
    return 0;
}

///
const int maxn=4e6+50;
struct node{
    ll h,w;
    bool operator<(const node &o)const{
        if(h==o.h)return w>o.w;
        else return h>o.h;
    }
}a[maxn];

ll dp[maxn];
int q[maxn];
int head,tail;
ll getDP(int x,int i){
    return dp[x]+a[x+1].h*a[i].w;
}
ll getB(int x,int y){ ///1 2
    return dp[x]-dp[y];
}
ll getK(int x,int y){
    return a[y+1].h-a[x+1].h;
}
int main()
{
    std::ios::sync_with_stdio(false);
    int n;
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a[i].h>>a[i].w;
    }
    sort(a+1,a+1+n);
    int mi=0;
    int cnt=0;
    for(int i=1;i<=n;i++){
        if(a[i].w>mi){
            a[++cnt]=a[i];mi=a[i].w;
        }
    }
    n=cnt;
    //dp[1]=a[1].w*a[1].h;
    head=tail=0;
    q[++tail]=0;
    for(int i=1;i<=n;i++){
        while(head+2<=tail&&getDP(q[head+2],i)<=getDP(q[head+1],i))
            head++;
       // cout<<"q["<<head+1<<"]="<<q[head+1]<<endl;
        dp[i]=getDP(q[head+1],i);
        while(head+2<=tail&&getB(q[tail-1],q[tail])*getK(q[tail],i)>=getB(q[tail],i)*getK(q[tail-1],q[tail]))
            tail--;
        q[++tail]=i;
       // cout<<"dp["<<i<<"]="<<dp[i]<<endl;
    }
    cout<<dp[n]<<endl;
    return 0;
}

博弈

威佐夫博弈

scanf("%lld%lld",&a,&b);
   if(a>b) swap(a,b);
   int temp=abs(a-b);
   int ans=temp*(1.0+sqrt(5.0))/2.0;
   if(ans==a) printf("0");//先手必败
   else       printf("1");
   return 0;

sg函数

int sg[maxn];
int vis[1500];
int getSG(int x){
    sg[0]=0;
    for(int i=1;i<=x;i++){
        memset(vis,0,sizeof(vis));
        for(int j=1;fib[j]<=i;j++)
            vis[sg[i-fib[j]]]=1;
        for(int j=0;j<=x;j++){
            if(vis[j]==0){
                sg[i]=j;break;
            }
        }
    }
}

ST表

int d[maxn][20],a[maxn],n;
int lg[maxn];
void init(){
    for(int i=1;i<=n;i++)d[i][0]=i;
    for(int j=1;(1<<j)<=n;j++){
        for(int i=1;i+(1<<j)-1<=n;i++){
            d[i][j]=(a[d[i][j-1]]>=a[d[i+(1<<(j-1))][j-1]])?
            d[i][j-1]:d[i+(1<<(j-1))][j-1];
        }
    }
}
    lg[0]=-1;
    for(int i=1;i<maxn;i++)lg[i]=lg[i>>1]+1;
	int k=lg[R-L+1];
    if(a[d[R-(1<<k)+1][k]]>a[d[L][k]])
        mid=d[R-(1<<k)+1][k];

枚举子集

1	for(int j=x;j;j=(j-1)&x) //枚举所有x的二进制子集

SOSDP

for(int i=0;i<4;i++){   ///n*logn 遍历所有子集
    for(int j=0;j<(1<<4);j++){
        if((j&(1<<i))==0){
            bitset<4> a(j);
            cout<<"i="<<i<<" pre="<<a<<" nex=";
            a.set(i);
            cout<<a.set(i)<<endl;
            v[j|(1<<i)].push_back(j);
            dp[j|(1<<i)]=max(dp[j|(1<<i)],dp[j]);
        }
    }
}

Prufer序列

理论

一棵n个节点的无根树唯一地对应了一个长度为n-2的数列，数列中的每个数都在1到n的范围内。

上面这句话比较重要。通过上面的定理，

1）我们可以直接推出n个点的无向完全图的生成树的计数：n^(n-2)   即n个点的有标号无根树的计数。

 

2）一个有趣的推广是，n个节点的度依次为D1, D2, …, Dn的无根树共有   (n-2)! / [ (D1-1)!(D2-1)!..(Dn-1)! ]  个，因为此时Prüfer编码中的数字i恰好出现Di-1次。

即 n种元素，共n-2个，其中第i种元素有Di-1个，求排列数。

 

3）n个节点的度依次为D1, D2, …, Dn，令有m个节点度数未知，求有多少种生成树？(BZOJ1005 明明的烦恼)

令每个已知度数的节点的度数为di，有n个节点，m个节点未知度数，left=(n-2)-(d1-1)-(d2-1)-...-(dk-1)

已知度数的节点可能的组合方式如下

(n-2)!/(d1-1)!/(d2-1)!/.../(dk-1)!/left!

剩余left个位置由未知度数的节点随意填补，方案数为m^left

于是最后有

ans=(n-2)!/(d1-1)!/(d2-1)!/.../(dk-1)!/left! * m^left

n个点的 有标号有根树的计数：n^(n-2)*n = n^(n-1)

prufer数列是一种无根树的编码表示，类似于hash。

一棵n个节点带编号的无根树，对应唯一串长度为n-2的prufer编码。所以一个n阶完全图的生成树个数就是n^(n-2)

首先定义无根树中度数为1的节点是叶子节点。

找到编号最小的叶子并删除，序列中添加与之相连的节点编号，重复执行直到只剩下2个节点。
	for (int i = 1; i <= n; i++) {
		if (degree[i] == 1) {
			gg.insert (i);
			vis[i] = 1;
		}
	}
 
	set<int>::iterator it;
	int prufer[maxn], id = 0;
	for (; id <= n-3;) {
		int u = (*(it = gg.begin ()));
		gg.erase (u);
		for (int i = head[u]; i != -1; i = edge[i].next) {
			int v = edge[i].v;
			if (vis[v])
				continue;
			degree[v]--;
			prufer[++id] = v;
			if (degree[v] == 1) {
				gg.insert (v);
				vis[v] = 1;
			}
		}
	}
	for (int i = 1; i <= id; i++) {
		cout << prufer[i] << " ";
	} cout << endl;

（2）prufer序列转化为无根树。
设点集V={1,2,3,...,n}，每次取出prufer序列中最前面的元素u，在V中找到编号最小的没有在prufer序列中出现的元素v，给u，v连边然后分别删除，最后在V中剩下两个节点，给它们连边。最终得到的就是无根树。

具体实现也可以用一个set，维护prufer序列中没有出现的编号。复杂度O(nlgn)。

int n;
int prufer[maxn], node[maxn], cnt;
set<int> gg; //在prufer序列里没有出现的点
int vis[maxn]; //这个点是不是在prufer序列里面
bool used[maxn]; //这个点有没有使用过

	gg.clear ();
	memset (vis, 0, sizeof vis);
	memset (used, 0, sizeof used);
	cnt = 0;
	for (int i = 1; i <= n-2; i++) {
		cin >> prufer[i];
		vis[prufer[i]]++;
	}
	for (int i = 1; i <= n; i++) {
		if (!vis[i]) {
			gg.insert (i);
		}
	}
	set<int>::iterator it;
	for (int i = 1; i <= n-2; i++) {
		int v = (*(it = gg.begin ())), u = prufer[i];
		cout << u << "-" << v << endl;
		used[v] = 1;
		gg.erase (v);
		vis[u]--;
		if (!vis[u] && !used[u]) {
			gg.insert (u);
		}
	}
	it = gg.begin ();
	cout << *it << "-" << *(++it) << endl;

最后有一个很重要的性质就是prufer序列中某个编号出现的次数+1就等于这个编号的节点在无根树中的度数。

技巧

JAVA

import java.math.BigDecimal;
import java.math.BigInteger;
import java.util.Scanner;

        Scanner cin=new Scanner(System.in);

        BigInteger num1=new BigInteger("12345");
        BigInteger num2=cin.nextBigInteger();

        BigDecimal num3=new BigDecimal("123.45");
        BigDecimal num4=cin.nextBigDecimal();
import java.math.BigInteger;

public class Main {
    public static void main(String[] args) {
        BigInteger num1=new BigInteger("12345");
        BigInteger num2=new BigInteger("45");
        //加法
        System.out.println(num1.add(num2));
        //减法
        System.out.println(num1.subtract(num2));
        //乘法
        System.out.println(num1.multiply(num2));
        //除法(相除取整)
        System.out.println(num1.divide(num2));
        //取余
        System.out.println(num1.mod(num2));
        //最大公约数GCD
        System.out.println(num1.gcd(num2));
        //取绝对值
        System.out.println(num1.abs());
        //取反
        System.out.println(num1.negate());
        //取最大值
        System.out.println(num1.max(num2));
        //取最小值
        System.out.println(num1.min(num2));
        //是否相等
        System.out.println(num1.equals(num2));
    }
}
import java.math.BigDecimal;

public class Main {
    public static void main(String[] args) {
        BigDecimal num1=new BigDecimal("123.45");
        BigDecimal num2=new BigDecimal("4.5");
        //加法
        System.out.println(num1.add(num2));
        //减法
        System.out.println(num1.subtract(num2));
        //乘法
        System.out.println(num1.multiply(num2));
        //除法（在divide的时候就设置好要精确的小数位数和舍入模式）
        System.out.println(num1.divide(num2,10,BigDecimal.ROUND_HALF_DOWN));
        //取绝对值
        System.out.println(num1.abs());
        //取反
        System.out.println(num1.negate());
        //取最大值
        System.out.println(num1.max(num2));
        //取最小值
        System.out.println(num1.min(num2));
        //是否相等
        System.out.println(num1.equals(num2));
        //判断大小( > 返回1, < 返回-1)
        System.out.println(num2.compareTo(num1));
    }
}
while(cin.hasNext())//相当于EOF
二分求开根号
static BigInteger cal(BigInteger x){
        BigInteger l = BigInteger.ONE ;
        BigInteger r = x ;
        BigInteger temp = BigInteger.ZERO ;
        while(!l.equals(r)){
            BigInteger mid = (l.add(r)).divide(BigInteger.valueOf(2)) ;
            if(temp.compareTo(BigInteger.ZERO)!=0&&temp.compareTo(mid)==0){
                break ;
            }else{
                temp = mid ;
            }
            if(temp.compareTo(BigInteger.ZERO)==0){
                temp = mid ;
            }
            if(mid.multiply(mid).compareTo(x)==1){
                r=mid ;
            }else{
                l=mid ;
            }
        }
        if(l.multiply(l).compareTo(x)==1){
            l=l.subtract(BigInteger.ONE) ;
        }
        return l;
        
}
牛顿迭代求平方根
      static BigInteger cal(BigInteger x) {
          BigInteger ans=BigInteger.valueOf(0);
          if(x.equals(BigInteger.valueOf(0))==true)return ans;
          BigInteger r=BigInteger.valueOf(1);
          BigInteger l=BigInteger.valueOf(-1);
          while(true) {
              BigInteger nxt =r.add(x.divide(r)).shiftRight(1);
              if(nxt.equals(l)==true) {
                  if(l.compareTo(r)==-1)return r;
                  else return l;
              }
              l=r;r=nxt;
          }

      }

文件读入

1 2	freopen("input.txt","r",stdin); freopen("output.txt","w",stdout);

扩栈

1 2	// 解决爆栈问题 #pragma comment(linker, "/STACK:1024000000,1024000000")

快速读入

// 适用于正负整数
template <class T>
inline bool scan_d(T &ret)
{
    char c;
    int sgn;
    if (c = getchar(), c == EOF) return 0; //EOF
    while (c != '-' && (c < '0' || c > '9')) c = getchar();
    sgn = (c == '-') ? -1 : 1;
    ret = (c == '-') ? 0 : (c - '0');
    while (c = getchar(), c >= '0' && c <= '9') ret = ret * 10 + (c - '0');
    ret *= sgn;
    return 1;
}
inline void out(int x)
{
    if (x > 9) out(x / 10);
    putchar(x % 10 + '0');
}

莫队算法

// ---
// 莫队算法,可以解决一类静态,离线区间查询问题。分成 $\sqrt{x}$ 块,分块排序。
// ---
struct query { int L, R, id; };
void solve(query node[], int m)
{
    memset(ans, 0, sizeof(ans));
    sort(node, node + m, [](query a, query b) {
        return a.l / unit < b.l / unit
               || a.l / unit == b.l / unit && a.r < b.r;
    });
    int L = 1, R = 0;
    for (int i = 0; i < m; i++)
    {
        while (node[i].L < L) add(a[--L]);
        while (node[i].L > L) del(a[L++]);
        while (node[i].R < R) del(a[R--]);
        while (node[i].R > R) add(a[++R]);
        ans[node[i].id] = tmp;
    }
}

//带修莫队，复杂度n^{5/3}
struct query{
    int id,l,r,x;
}Q[maxn];
struct update{
    int pos,val,rval;
}C[maxn];
void ac(){
    unit=pow(n,2.0/3.0);
    sort(Q+1,Q+1+q1,[](query a,query b){
        if(a.l/unit!=b.l/unit)return a.l/unit<b.l/unit;
        if(a.r/unit!=b.r/unit)return b.r/unit<b.r/unit;
        return a.x<b.x;
    });
    int L=1,R=0,X=0;
    for(int i=1;i<=q1;i++){
        while(Q[i].l>L)del(a[L++]);
        while(Q[i].l<L)add(a[--L]);
        while(Q[i].r>R)add(a[++R]);
        while(Q[i].r<R)del(a[R--]);
        while(Q[i].x<X)remove(i,X--);
        while(Q[i].x>X)insert(i,++X);
        ans[Q[i].id]=p;
    }
}

cdq分治

///矩形区间加 区间求和
struct node{
    int x1,y1,op,id;
}Q[maxn],q[maxn];ll c[MV];
int lowbit(int x){return x&(-x);}
void add(int x,int v){
    for(;x<MV;x+=lowbit(x))c[x]+=v;
}
ll sum(int x){
    ll ans=0;for(;x;x-=lowbit(x))ans+=c[x];return ans;
}
void cdq(int l,int r){
    if(l==r)return;int mid=(l+r)>>1;
    int lq=l,rq=mid+1,cnt1=0;
    cdq(l,mid);cdq(mid+1,r);
    while(lq<=mid&&rq<=r){
        if(Q[lq].x1<=Q[rq].x1){
            if(Q[lq].op==1)add(Q[lq].y1,Q[lq].id);
            q[++cnt1]=Q[lq];lq++;
        }
        else{
            if(Q[rq].op==2){
                ans[Q[rq].id]+=sum(Q[rq].y1);
            }
            else if(Q[rq].op==3){
                ans[Q[rq].id]-=sum(Q[rq].y1);
            }
            q[++cnt1]=Q[rq];rq++;
        }
    }
    while(rq<=r){
        if(Q[rq].op==2){
            ans[Q[rq].id]+=sum(Q[rq].y1);
        }
        else if(Q[rq].op==3){
            ans[Q[rq].id]-=sum(Q[rq].y1);
        }
        q[++cnt1]=Q[rq];rq++;
    }
    while(lq<=mid){
        if(Q[lq].op==1)add(Q[lq].y1,Q[lq].id);
        q[++cnt1]=Q[lq];lq++;
    }
    for(int i=l;i<=mid;i++)if(Q[i].op==1)add(Q[i].y1,-Q[i].id);
    for(int i=1;i<=cnt1;i++){
        Q[i+l-1]=q[i];
    }
}
int main()
{
    cin>>s>>w;
    while(true){
        cin>>op;
        if(op==1){
            int x,y,a;
            cin>>x>>y>>a;x++;y++;
            Q[++cnt]={x,y,1,a};
        }
        else if(op==2){
            int x1,y1,x2,y2;
            cin>>x1>>y1>>x2>>y2;x1++;y1++;x2++;y2++;
            Q[++cnt]={x1-1,y1-1,2,++m};
            Q[++cnt]={x2,y2,2,m};
            Q[++cnt]={x1-1,y2,3,m};
            Q[++cnt]={x2,y1-1,3,m};
        }
        else break;
    }
    cdq(1,cnt);

整体二分

///带修查区间第K大
#include<iostream>
typedef long long ll;
using namespace std;
const ll inf=1e18;
const int maxn=2e5+10;
const ll mod=1e9+7;
//#define endl '\n'
int a[maxn],cnt,tot,n,m;;
int ans[maxn],c[maxn];
struct Q{
    int l,r,k,id,op;
}q[maxn*3],q2[maxn*3],q1[maxn*3];
int lowbit(int x){return x&(-x);}
void add(int x,int v){
    for(;x<=n;x+=lowbit(x))c[x]+=v;
}
int sum(int x){
    int ans=0;
    for(;x;x-=lowbit(x))ans+=c[x];return ans;
}
void solve(int l,int r,int ql,int qr){
    if(ql>qr)return;
    if(l==r){
        for(int i=ql;i<=qr;i++){
            if(q[i].op==2)ans[q[i].id]=l;
        }
        return;
    }
    int mid=(l+r)>>1,cnt1=0,cnt2=0,x;
    for(int i=ql;i<=qr;i++){
        if(q[i].op==1){
            if(q[i].l<=mid)q1[++cnt1]=q[i],add(q[i].id,q[i].r);
            else q2[++cnt2]=q[i];
        }
        else{
            x=sum(q[i].r)-sum(q[i].l-1);
            if(q[i].k<=x)q1[++cnt1]=q[i];
            else q[i].k-=x,q2[++cnt2]=q[i];
        }
    }
    for(int i=1;i<=cnt1;i++)
        if(q1[i].op==1)add(q1[i].id,-q1[i].r);
    for(int i=1;i<=cnt1;i++)q[ql+i-1]=q1[i];
    for(int i=1;i<=cnt2;i++)q[ql+i+cnt1-1]=q2[i];
    solve(l,mid,ql,ql+cnt1-1);
    solve(mid+1,r,ql+cnt1,qr);
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);std::cout.tie(0);
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>a[i],q[++cnt]={a[i],1,0,i,1};
    for(int i=1;i<=m;i++){
        char op;cin>>op;
        if(op=='Q'){
            int l,r,k;cin>>l>>r>>k;q[++cnt]={l,r,k,++tot,2};
        }
        else{
            int x,t;cin>>x>>t;
            q[++cnt]={a[x],-1,0,x,1};q[++cnt]={a[x]=t,1,0,x,1};
        }
    }
    solve(-1e9,1e9,1,cnt);
    for(int i=1;i<=tot;i++)cout<<ans[i]<<endl;
    return 0;
}

高精度

// 加法 乘法 小于号 输出
struct bint
{
    int l;
    short int w[100000];
    bint(ll x = 0)
    {
        l = x == 0, memset(w, 0,sizeof(w));
        while (x) w[l++] = x % 10, x /= 10;
    }
    bool operator<(const bint& x) const
    {
        if (l != x.l) return l < x.l;
        int i = l - 1;
        while (i >= 0 && w[i] == x.w[i]) i--;
        return (i >= 0 && w[i] < x.w[i]);
    }
    bint operator+(const bint& x) const
    {
        bint ans;
        ans.l = l > x.l ? l : x.l;
        for (int i = 0; i < ans.l; i++)
        {
            ans.w[i] += w[i] + x.w[i];
            ans.w[i + 1] += ans.w[i] / 10;
            ans.w[i] = ans.w[i] % 10;
        }
        if (ans.w[ans.l] != 0) ans.l++;
        return ans;
    }
    bint operator*(const bint& x) const
    {
        bint res;
        int up, tmp;
        for (int i = 0; i < l; i++)
        {
            up = 0;
            for (int j = 0; j < x.l; j++)
            {
                tmp = w[i] * x.w[j] + res.w[i + j] + up;
                res.w[i + j] = tmp % 10;
                up = tmp / 10;
            }
            if (up != 0) res.w[i + x.l] = up;
        }
        res.l = l + x.l;
        while (res.w[res.l - 1] == 0 && res.l > 1) res.l--;
        return res;
    }
    void print()
    {
        for (int i = l - 1; ~i; i--) printf("%d", w[i]);
        puts("");
    }
};

矩阵

矩阵快速幂

typedef vector<ll>vec;
typedef vector<vec>mat;
mat mul(mat& A,mat &B){
    mat C(A.size(),vec(B[0].size()));
    for(int i=0;i<A.size();i++)
        for(int k=0;k<B.size();k++)
        if(A[i][k])
            for(int j=0;j<B[0].size();j++)
            C[i][j]=(C[i][j]+A[i][k]*B[k][j]%mod+mod)%mod;
    return C;
}
mat Pow(mat A,ll n){
    mat B(A.size(),vec(A.size()));
    for(int i=0;i<A.size();i++)B[i][i]=1;
    for(;n;n>>=1,A=mul(A,A))
        if(n&1)B=mul(B,A);
    return B;
}

高斯消元

void gauss()
{
    int now = 1, to;
    double t;
    for (int i = 1; i <= n; i++, now++)
    {
        /*for (to = now; !a[to][i] && to <= n; to++);
        //做除法时减小误差，可不写
        if (to != now)
            for (int j = 1; j <= n + 1; j++)
                swap(a[to][j], a[now][j]);*/
        t = a[now][i];
        for (int j = 1; j <= n + 1; j++) a[now][j] /= t;
        for (int j = 1; j <= n; j++)
            if (j != now)
            {
                t = a[j][i];
                for (int k = 1; k <= n + 1; k++) a[j][k] -= t * a[now][k];
            }
    }
}
int gauss(int n,int m){
   int col, i, mxr, j, row;
   for (row = col = 1; row <= n && col <= m;row++,col++){
      mxr = row;
      for (i = row + 1; i <= n;i++)
      if(fabs(a[i][col])>fabs(a[mxr][col]))
         mxr = i;
      if(mxr!=row)
         swap(a[row], a[mxr]);
      if(fabs(a[row][col])<eps){
         row--;
         continue;
      }
      for (i = 1; i <= n;i++) /////消成上三角矩阵
         if(i!=row&&fabs(a[i][col])>eps)
            for (j = m; j >= col;j--)
               a[i][j] -= a[row][j] / a[row][col] * a[i][col];
         
   }
   row--;
   for (i = row; i >= 1;i--){//////回代成对角矩阵
      for (j = i + 1; j <= row;j++){
         a[i][m] -= a[j][m] * a[i][j];
      }
      a[i][m] /= a[i][i];
   }
   return row;
}

数位DP

int num[20];
int dp[20][2];
int dfs(int pos,int pre,int sta,bool first){
    if(pos==-1)return 1;
    if(!first&&dp[pos][sta]!=-1)return dp[pos][sta];
    int up=first?num[pos]:9;
    int ans=0;
    for(int i=0;i<=up;i++){
        if(pre==6&&i==2)continue;
        if(i==4)continue;
        ans+=dfs(pos-1,i,i==6,first&&i==num[pos]);
    }
    if(!first)dp[pos][sta]=ans;
    return ans;
}
int ac(int x){
    int pos=0;
    while(x){
        num[pos++]=x%10;
        x/=10;
    }
    return dfs(pos-1,-1,0,true);
}

Mediocre String Problem （2018南京M,回文+LCP 3×3=9种做法 %%%千年好题感谢"Grunt"大佬的细心讲解）

Diposting di 2019-04-24 | Edited on 2018-11-29

题意

给出一个串S,和一个串T.

要求从S串中取一个子串，后面接上T串的一个前缀组成一个结果串，（要求S串的部分比T串的部分长）

其中，S串贡献的部分可以分成两部分，S1+S2;

前面的S1 是T部分的反转；

S2 就只能是回文串，因为S串的部分必须比T的多，所以S2长度必须大于等于1

然后我们可以分成两部分，首先先把S中的所有回文串求出，可以用（回文树/马拉车/字符串哈希）

对于每一个回文串，它的左边半径部分都可以作为S1的右端点，除了中心，而且边缘也可以吃到一个

比如 CABABA 其中回文串中心是第二个A，S1的右端点可以是CAB 注意C也可以的哦

然后找出这个端点剩下的就是求S1和T的lcp的长度了，根据题意每一个长度都一个贡献一个符合要求的答案

针对这个问题我们可以把S 反转和T用EXKMP 求lcp （也可以用后缀数组/字符串哈希/exkmp/后缀自动机）

所以这题的解法大概有（3×3=9 或者3×4=12）种。

做法1 :马拉车+EXKMP

///感谢Grunt 大佬的细心讲解
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
char s[maxn],t[maxn];
int lens,lent;
int mynext[maxn];
int extend[maxn];
ll sum[maxn];
void pre_EKMP(char x[],int m,int next[]){
    next[0]=m;
    int j=0;
    while(j+1<m&&x[j]==x[j+1])j++;
    next[1]=j;
    int k=1;
    for(int i=2;i<m;i++){
        int p=next[k]+k-1;
        int L=next[i-k];
        if(i+L<p+1)next[i]=L;
        else{
            j=max(0,p-i+1);
            while(i+j<m&&x[i+j]==x[j])j++;
            next[i]=j;
            k=i;
        }
    }
}
void EKMP(char x[],int m,char y[],int n,int next[],int extend[]){
    pre_EKMP(x,m,next);
    int j=0;
    while(j<n&&j<m&&x[j]==y[j])j++;
    extend[0]=j;
    int k=0;
    for(int i=1;i<n;i++){
        int p=extend[k]+k-1;
        int L=next[i-k];
        if(i+L<p+1)extend[i]=L;
        else{
            j=max(0,p-i+1);
            while(i+j<n&&j<m&&y[i+j]==x[j])j++;
            extend[i]=j;
            k=i;
        }
    }
}
char Ma[maxn*2];
int Mp[maxn*2];
void Manacher(char s[],int len){
    int l=0;
    Ma[l++]='$';
    Ma[l++]='#';
    for(int i=0;i<len;i++){
        Ma[l++]=s[i];
        Ma[l++]='#';
    }
    Ma[l]=0;
    int mx=0,id=0;
    for(int i=0;i<l;i++){
        Mp[i]=mx>i?min(Mp[2*id-i],mx-i):1;
        while(Ma[i+Mp[i]]==Ma[i-Mp[i]])Mp[i]++;
        if(i+Mp[i]>mx){
            mx=i+Mp[i];
            id=i;
        }
    }
}
ll getsum(int l,int r){
    if(l>r)return 0;
    else if(l<=0)return sum[r];
    else return sum[r]-sum[l-1];
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    cin>>s>>t;
    lens=strlen(s);lent=strlen(t);
    Manacher(s,lens);
    reverse(s,s+lens);
    EKMP(t,lent,s,lens,mynext,extend);
    reverse(extend,extend+lens);
    sum[0]=extend[0];
    for(int i=1;i<lens;i++){
        sum[i]=sum[i-1]+extend[i];
    }
    ll ans=0;                                     ///0 1 2 3 4
    for(int i=2;i<2*lens+3;i++){                  ///a b a b a
        int cnt=Mp[i]-1;      ///6-1=5;            $ # a # b # a # b # a #
        if(cnt==0||Mp[i]==0)continue;           ///0 1 2 3 4 5 6 7 8 9 10 11
        if(cnt&1){///奇数长度的回文 例如ababa  MP= 1 1 2 1 4 1 6 1 4 1  2  1  0
            int where=(i-2)/2;  ///找到a这个位置 =(6-1)/2=2;
            int r=where-1;      ///然后从a前面一个位置b作为右端点 =1
            int l=where-Mp[i]/2; ///然后找到左端点=2-6/2 =-1
            ans+=getsum(l,r);
        }
        else{                 /// 偶数的  例如aabbaa
            int where=(i-2-1)/2;   /// 找到b#b中间的‘#’ 左边的b
            int r=where-1;         ///右端点
            int l=where-cnt/2;    /// 左端点
            ans+=getsum(l,r);
        }
    }
    cout<<ans<<endl;
    return 0;
}

做法2. 回文自动机+EXKMP

附上大佬的题解：

M.Mediocre String Problem

题意：给S串与T串。S[i..j]+T[1..k]为回文串，且|S[i..j]|>|T[1..k]|，求(i,j,k)个数。

将S[i..j]分为两个部分，S[i..p]为T[1..k]的反转，S[p+1..j]为回文串。

由于|S[i..j]|>|T[1..k]|，所以S[p+1..j]必须不为空。

枚举回文串的起始点p+1，那么我们要求的是：

1.由于S[i..p]为T[1..k]的反转，我们只要求有多少个(i,k)。这个部分是exkmp的基础。

将S反转，跟T跑exkmp，求出ex[]，再把ex[]反过来即可。

2.S[p+1..j]为回文串，我们只要求有多少个j，即求的是以p+1为起点的回文串个数cnt[]。

那么只要把S串倒着插入回文自动机，cnt[i]=插入第i个字符后，fail树的深度。

最后枚举回文串起点p+1，算出ex[p]*cnt[p+1]，求和即为答案。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
char s[maxn],t[maxn];
int lens,lent;
int mynext[maxn];
int extend[maxn];
int num[maxn];
void pre_EKMP(char x[],int m,int next[]){
    next[0]=m;
    int j=0;
    while(j+1<m&&x[j]==x[j+1])j++;
    next[1]=j;
    int k=1;
    for(int i=2;i<m;i++){
        int p=next[k]+k-1;
        int L=next[i-k];
        if(i+L<p+1)next[i]=L;
        else{
            j=max(0,p-i+1);
            while(i+j<m&&x[i+j]==x[j])j++;
            next[i]=j;
            k=i;
        }
    }
}
void EKMP(char x[],int m,char y[],int n,int next[],int extend[]){
    pre_EKMP(x,m,next);
    int j=0;
    while(j<n&&j<m&&x[j]==y[j])j++;
    extend[0]=j;
    int k=0;
    for(int i=1;i<n;i++){
        int p=extend[k]+k-1;
        int L=next[i-k];
        if(i+L<p+1)extend[i]=L;
        else{
            j=max(0,p-i+1);
            while(i+j<n&&j<m&&y[i+j]==x[j])j++;
            extend[i]=j;
            k=i;
        }
    }
}
struct Palindromic_Tree{
    int next[maxn][26];
    int fail[maxn];
    int cnt[maxn];
    int num[maxn];
    int len[maxn];
    int S[maxn];
    int last;
    int n;
    int p;
    int newnode(int l){
        for(int i=0;i<26;i++)next[p][i]=0;
        cnt[p]=num[p]=0;len[p]=l;
        return p++;
    }
    void init(){
        p=0;
        newnode(0);
        newnode(-1);
        last=n=0;
        S[n]=-1;
        fail[0]=1;
    }
    int getfail(int x){
        while(S[n-len[x]-1]!=S[n])x=fail[x];
        return x;
    }
    int add(int c){
        c-='a';
        S[++n]=c;
        int cur=getfail(last);
        if(!next[cur][c]){
            int now=newnode(len[cur]+2);
            fail[now]=next[getfail(fail[cur])][c];
            next[cur][c]=now;
            num[now]=num[fail[now]]+1;
        }
        last=next[cur][c];
        cnt[last]++;
        return num[last];
    }
    void count(){
        for(int i=p-1;i>=0;i--)cnt[fail[i]]+=cnt[i];
    }
}pam;
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    cin>>s>>t;
    lens=strlen(s);lent=strlen(t);
    pam.init();
    for(int i=lens-1;i>=0;i--){
        num[i]=pam.add(s[i]);
    }
    reverse(s,s+lens);
    EKMP(t,lent,s,lens,mynext,extend);
    reverse(extend,extend+lens);
    ll ans=0;
    for(int i=0;i<lens-1;i++){
        ans+=1LL*extend[i]*num[i+1];
    }
    cout<<ans<<endl;
    return 0;
}

做法3.后缀数组+回文自动机（498ms)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
struct DA{
    #define F(x) ((x)/3+((x)%3==1?0:tb))
    #define G(x) ((x)<tb?(x)*3+1:((x)-tb)*3+2)
    int sa[maxn*20],rank[maxn*20],height[maxn*20],str[maxn*20];
    int wa[maxn*20],wb[maxn*20],wv[maxn*20],wss[maxn*20];
    int c0(int *r,int a,int b){
        return r[a]==r[b]&&r[a+1]==r[b+1]&&r[a+2]==r[b+2];
    }
    int c12(int k,int *r,int a,int b){
        if(k==2)
            return r[a]<r[b]||(r[a]==r[b]&&c12(1,r,a+1,b+1));
        else return r[a]<r[b]||(r[a]==r[b]&&wv[a+1]<wv[b+1]);
    }
    void sort(int *r,int *a,int *b,int n,int m){
        int i;
        for(i=0;i<n;i++)wv[i]=r[a[i]];
        for(i=0;i<m;i++)wss[i]=0;
        for(i=0;i<n;i++)wss[wv[i]]++;
        for(i=1;i<m;i++)wss[i]+=wss[i-1];
        for(i=n-1;i>=0;i--)
            b[--wss[wv[i]]]=a[i];
    }
    void dc3(int *r,int *sa,int n,int m){
        int i,j,*rn=r+n;
        int *san=sa+n,ta=0,tb=(n+1)/3,tbc=0,p;
        r[n]=r[n+1]=0;
        for(i=0;i<n;i++)if(i%3!=0)wa[tbc++]=i;
        sort(r+2,wa,wb,tbc,m);
        sort(r+1,wb,wa,tbc,m);
        sort(r,wa,wb,tbc,m);
        for(p=1,rn[F(wb[0])]=0,i=1;i<tbc;i++)
            rn[F(wb[i])]=c0(r,wb[i-1],wb[i])?p-1:p++;
        if(p<tbc)dc3(rn,san,tbc,p);
        else for(i=0;i<tbc;i++)san[rn[i]]=i;
        for(i=0;i<tbc;i++)if(san[i]<tb)wb[ta++]=san[i]*3;
        if(n%3==1)wb[ta++]=n-1;
        sort(r,wb,wa,ta,m);
        for(i=0;i<tbc;i++)wv[wb[i]=G(san[i])]=i;
        for(i=0,j=0,p=0;i<ta&&j<tbc;p++)
            sa[p]=c12(wb[j]%3,r,wa[i],wb[j])?wa[i++]:wb[j++];
        for(;i<ta;p++)sa[p]=wa[i++];
        for(;j<tbc;p++)sa[p]=wb[j++];
    }
    void da(int n,int m){
        for(int i=n;i<n*3;i++)str[i]=0;
        dc3(str,sa,n+1,m);
        int i,j,k=0;
        for(i=0;i<=n;i++)rank[sa[i]]=i;
        for(i=0;i<n;i++){
            if(k)k--;
            j=sa[rank[i]-1];
            while(str[i+k]==str[j+k])k++;
            height[rank[i]]=k;
        }
    }
    void print(int n){
        cout<<"sa[] ";
        for(int i=0;i<=n;i++)cout<<sa[i]<<" ";cout<<endl;
        cout<<"rank[] ";
        for(int i=0;i<=n;i++)cout<<rank[i]<<" ";cout<<endl;
        cout<<"height[] ";
        for(int i=0;i<=n;i++)cout<<height[i]<<" ";cout<<endl;
    }
}DA;
struct PalTree{
    int next[maxn][26],fail[maxn],cnt[maxn],num[maxn],len[maxn],S[maxn],last,n,p;
    int newnode(int l){
        for(int i=0;i<26;i++)next[p][i]=0;
        cnt[p]=num[p]=0;len[p]=l;return p++;
    }
    void init(){
        p=0;newnode(0);newnode(-1);last=0;n=0;S[n]=-1;fail[0]=1;
    }
    int get_fail(int x){
        while(S[n-len[x]-1]!=S[n])x=fail[x];return x;
    }
    int add(int c){
        c-='a';S[++n]=c;int cur=get_fail(last);
        if(!next[cur][c]){
            int now=newnode(len[cur]+2);
            fail[now]=next[get_fail(fail[cur])][c];
            next[cur][c]=now;num[now]=num[fail[now]]+1;
        }
        last=next[cur][c];cnt[last]++;return num[last];
    }
    void count(){for(int i=p-1;i>=0;i--)cnt[fail[i]]+=cnt[i];}
}PAM;
char s[maxn],t[maxn];
int num[maxn],cnt[maxn];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    cin>>s>>t;
    int lens=strlen(s),lent=strlen(t);
    int len=0;PAM.init();
    for(int i=0;i<lens;i++)DA.str[len++]=s[lens-i-1]-'a'+1,cnt[lens-i-1]=PAM.add(s[lens-i-1]);
    DA.str[len++]=30;
    for(int i=0;i<lent;i++)DA.str[len++]=t[i]-'a'+1;
    DA.str[len]=0;
    DA.da(len,200);
	int p=DA.rank[lens+1];
	//DA.print(len);
	int now=len+1;
	for(int i=p-1;i>=0;i--){
		now=min(now,DA.height[i+1]);
		if(DA.sa[i]>=0&&DA.sa[i]<lens){
			num[lens-1-DA.sa[i]]=now;
		}
	}
	now=len+1;
	for(int i=p+1;i<=len;i++){
		now=min(now,DA.height[i]);
		if(DA.sa[i]>=0&&DA.sa[i]<lens){
			num[lens-1-DA.sa[i]]=now;
		}
	}
	ll ans=0;
    for(int i=0;i<lens-1;i++){
        ans+=1LL*num[i]*cnt[i+1];
    }
    cout<<ans<<endl;
    return 0;
}

感谢Grunt 大佬的细心讲解！！

///感谢Grunt 大佬的细心讲解

!(Mediocre String Problem/a.jpg)
毅种循环~
!(Mediocre String Problem/b.jpg)

数学基础

Diposting di 2019-04-24 | Edited on 2019-03-03

基本计数方法

Chess QueenUVA - 11538 (平方和公式由(n+1)^3推出)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+10;
const ll inf=0x3f3f3f3f3f3f3f3fLL;

int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    ll n,m;
    while(cin>>n>>m&&n&&m){
        if(n>m)swap(n,m);
        cout<<n*m*(m-1)+n*m*(n-1)+2*n*(n-1)*(3*m-n-1)/3<<endl;
    }
    return 0;
}

Triangle CountingUVA - 11401 (从1-n中取出三个不同整数组成三角形的方法)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+10;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
ll dp[maxn];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    dp[3]=0;
    for(ll x=4;x<=1e6;x++)
        dp[x]=dp[x-1]+((x-1)*(x-2)/2-(x-1)/2)/2;
    int n;
    while(cin>>n){
        if(n<3)break;
        cout<<dp[n]<<endl;
    }
    return 0;
}

Triangle CountingUVA - 11401（容斥定理）

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e6+7;
const int maxn=1e6+10;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int c[550][550];

int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    c[0][0]=1;
    for(int i=0;i<=500;i++){
        c[i][0]=c[i][i]=1;
        for(int j=1;j<i;j++)
            c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
    }
    int t;
    cin>>t;
    for(int cas=1;cas<=t;cas++){
        int n,m,k,sum=0;
        cin>>n>>m>>k;
        for(int sta=0;sta<(1<<4);sta++){
            int b=0,r=n,cc=m;
            if(sta&1)r--,b++;
            if(sta&2)r--,b++;
            if(sta&4)cc--,b++;
            if(sta&8)cc--,b++;
            if(b&1)sum=(sum-c[r*cc][k]+mod)%mod;
            else sum=(sum+c[r*cc][k])%mod;
        }
        cout<<"Case "<<cas<<": "<<sum<<endl;
    }
    return 0;
}

递推关系

Ingenuous CubrencyUVA - 11137 (背包)

题意

求将n写成诺干个正整数的立方和有多少种方案

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e6+7;
const int maxn=1e6+10;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
ll dp[maxn];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    dp[0]=1;
    for(int i=1;i<=21;i++){
        for(int j=0;j<=10000;j++){
            dp[i*i*i+j]+=dp[j];
        }
    }
    int n;
    while(cin>>n)cout<<dp[n]<<endl;
    return 0;
}

Exploring PyramidsUVALive - 3516 (记忆化搜索)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9;
const int maxn=1e6+10;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
char s[maxn];
ll dp[400][400];

ll dfs(int i,int j){
    if(i==j)return 1;
    if(s[i]!=s[j])return 0;
    ll &ans=dp[i][j];
    if(ans>=0)return ans;ans=0;
    for(int k=i+2;k<=j;k++)
        if(s[i]==s[k])
        ans=(ans+1LL*dfs(i+1,k-1)*1LL*dfs(k,j))%mod;
    return ans;
}

int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);

    while(cin>>s){
        memset(dp,-1,sizeof(dp));
        cout<<dfs(0,strlen(s)-1)<<endl;
    }
    return 0;
}

Investigating Div-Sum PropertyUVA - 11361 （数位DP）

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9;
const int maxn=1e6+10;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
ll dp[30][150][150];
int nu[30];
int k;
ll dfs(int pos,int num,int sum,bool limit){
    if(pos==-1)return (num%k==0)&&(sum%k==0);
    if(!limit&&dp[pos][num][sum]!=-1)return dp[pos][num][sum];
    int up=limit?nu[pos]:9;

    int ans=0;
    for(int i=0;i<=up;i++){
        ans+=dfs(pos-1,(num+i)%k,(sum*10+i)%k,limit&&i==nu[pos]);
    }
    if(!limit)dp[pos][num][sum]=ans;
    return ans;
}
ll ac(ll x){
    ll pos=0;
    while(x){
        nu[pos++]=x%10;
        x/=10;
    }
    return dfs(pos-1,0,0,true);
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int t;
    cin>>t;
    while(t--){
        ll a,b;
        cin>>a>>b>>k;
        if(k>90){
            cout<<0<<endl;continue;
        }
        memset(dp,-1,sizeof(dp));
        cout<<ac(b)-ac(a-1)<<endl;
    }
    return 0;
}
/*
999
1 1000 4

*/

数论

Always an integer UVALive - 4119 （欧拉函数）

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9;
const int maxn=4e6+10;
const ll inf=0x3f3f3f3f3f3f3f3fLL;

const int N = 4e6+10;
int phi[N] = {0, 1};
void caleuler()
{
    for (int i = 2; i < N; i++)
        if (!phi[i])
            for (int j = i; j < N; j += i)
            {
                if (!phi[j]) phi[j] = j;
                phi[j] = phi[j] / i * (i - 1);
            }
}
ll s[maxn],f[maxn];
void init(){
    caleuler();
    for(int i=1;i<N;i++){
        for(int j=i*2;j<N;j+=i)f[j]+=i*phi[j/i];
    }
    for(int i=2;i<N;i++)s[i]=s[i-1]+f[i];
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    init();
    int n;
    while(cin>>n&&n){
        cout<<s[n]<<endl;
    }
    return 0;
}

Emoogle GridUVA - 11916 （大步小步算法）

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e8+7;
const int maxn=550;
const ll inf=0x3f3f3f3f3f3f3f3fLL;

int n,m,k,b,r,x[maxn],y[maxn];
set<pair<int,int> >bset;

ll fastpow(ll a,ll n){
    ll ans=1;
    while(n){
        if(n&1)ans=(ans*a)%mod;
        a=(a*a)%mod;
        n>>=1;
    }
    return ans;
}

ll inv(ll a){
    return fastpow(a,mod-2);
}

ll mul_mod(ll a,ll b){
    return 1LL*a*b%mod;
}

int log_mod(int a,int b){
    int m,v,e=1,i;
    m=(int)sqrt(mod);
    v=inv(fastpow(a,m));
    map<int,int>x;
    x[1]=0;
    for(i=1;i<m;i++){
        e=mul_mod(e,a);
        if(!x.count(e))x[e]=i;
    }
    for(i=0;i<m;i++){
        if(x.count(b))return i*m+x[b];
        b=mul_mod(b,v);
    }
    return -1;
}

int count(){
    int c=0;
    for(int i=0;i<b;i++){
        if(x[i]!=m&&!bset.count(make_pair(x[i]+1,y[i])))c++;
    }
    c+=n;
    for(int i=0;i<b;i++)if(x[i]==1)c--;
    return mul_mod(fastpow(k,c),fastpow(k-1,1LL*n*m-b-c));
}

int doit(){
    int cnt=count();
    if(cnt==r)return m;

    int c=0;
    for(int i=0;i<b;i++)
        if(x[i]==m)c++;
    m++;
    cnt=mul_mod(cnt,fastpow(k,c));
    cnt=mul_mod(cnt,fastpow(k-1,n-c));
    if(cnt==r)return m;
    return log_mod(fastpow(k-1,n),mul_mod(r,inv(cnt)))+m;
}

int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int t;
    cin>>t;
    for(int p=1;p<=t;p++){
        cin>>n>>k>>b>>r;
        bset.clear();
        m=1;
        for(int i=0;i<b;i++){
            cin>>x[i]>>y[i];
            if(x[i]>m)m=x[i];
            bset.insert(make_pair(x[i],y[i]));
        }
        cout<<"Case "<<p<<": "<<doit()<<endl;
    }
    return 0;
}

组合游戏

Playing With StonesUVALive - 5059 (sg函数)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e8+7;
const int maxn=550;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
ll sg(ll x){
    return x%2==0?x/2:sg(x/2);
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int t;
    cin>>t;
    while(t--){
        ll n,a,v=0;
        cin>>n;
        for(int i=0;i<n;i++){
            cin>>a;
            v^=sg(a);
        }
        if(v)cout<<"YES\n";
        else cout<<"NO\n";
    }
    return 0;
}

洛谷试炼场 4-8单调队列

Diposting di 2019-04-24 | Edited on 2019-02-08

P2698 [USACO12MAR]花盆Flowerpot (二分+单调队列)

题解

二分区间

做两个单调队列记录最大最小值，如果差大于D就OK

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
struct node{
    int x,y;
    bool operator <(const node &a)const{
        return x<a.x;
    }
}a[maxn];
int n,d;
int qmax[maxn],qmin[maxn];
bool ok(int mid){
    int h1=1,h2=1,t1=0,t2=0;
    for(int i=1;i<=n;i++){
        while(h1<=t1&&a[i].y>a[qmax[t1]].y)t1--;
        qmax[++t1]=i;
        while(h2<=t2&&a[i].y<a[qmin[t2]].y)t2--;
        qmin[++t2]=i;
        while(h1<=t1&&a[i].x-a[qmax[h1]].x>mid)++h1;
        while(h2<=t2&&a[i].x-a[qmin[h2]].x>mid)++h2;
        if(a[qmax[h1]].y-a[qmin[h2]].y>=d)return true;
    }
    return false;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    cin>>n>>d;
    for(int i=1;i<=n;i++){
        cin>>a[i].x>>a[i].y;
    }
    sort(a+1,a+1+n);
    int ans=-1,l=0,r=1e8;
    while(l<=r){
        int mid=(l+r)/2;
        if(ok(mid)){
            ans=mid;
            r=mid-1;
        }
        else l=mid+1;
    }
    cout<<ans<<endl;
    return 0;
}

[HAOI2007]理想的正方形（二维单调队列）

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int value[1100][1100];
int qmin[1100],qmax[1100];
int hmin[1100][1100],hmax[1100][1100];
int lmin[1100][1100],lmax[1100][1100];
void print(int a,int b,int p[][1100]){
    for(int i=1;i<=a;i++){
        for(int j=1;j<=b;j++){
            cout<<p[i][j]<<" ";
        }
        cout<<endl;
    }
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int a,b,n;
    cin>>a>>b>>n;
    for(int i=1;i<=a;i++){
        for(int j=1;j<=b;j++){
            cin>>value[i][j];
        }
    }
    for(int i=1;i<=a;i++){
        int head1=1,tail2=0,head2=1,tail1=0;
        for(int j=1;j<=b;j++){
            while(head1<=tail1&&value[i][j]<value[i][qmin[tail1]])tail1--;qmin[++tail1]=j;
            while(head2<=tail2&&value[i][j]>value[i][qmax[tail2]])tail2--;qmax[++tail2]=j;
            while(j-qmin[head1]>=n)head1++;
            while(j-qmax[head2]>=n)head2++;
            if(j>=n)hmin[i][j-n+1]=value[i][qmin[head1]],hmax[i][j-n+1]=value[i][qmax[head2]];
        }
    }
   // cout<<endl;print(a,b,hmin);cout<<endl;print(a,b,hmax);cout<<endl;
    for(int i=1;i<=b-n+1;i++){
        int head1=1,tail2=0,head2=1,tail1=0;
        for(int j=1;j<=a;j++){
            while(head1<=tail1&&hmin[j][i]<hmin[qmin[tail1]][i])tail1--;qmin[++tail1]=j;
            while(head2<=tail2&&hmax[j][i]>hmax[qmax[tail2]][i])tail2--;qmax[++tail2]=j;
            while(j-qmin[head1]>=n)head1++;
            while(j-qmax[head2]>=n)head2++;
            if(j>=n)lmin[j-n+1][i]=hmin[qmin[head1]][i],lmax[j-n+1][i]=hmax[qmax[head2]][i];
        }
    }
  //  print(a,b,lmin);cout<<endl;print(a,b,lmax);
    int ans=inf;
    for(int i=1;i<=a-n+1;i++)
        for(int j=1;j<=b-n+1;j++)
            ans=min(ans,lmax[i][j]-lmin[i][j]);
    cout<<ans<<endl;
    return 0;
}

P2564 [SCOI2009]生日礼物（尺取法）

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
struct node{
    int kind;
    ll x;
    bool operator<(const node &a)const{
        return x<a.x;
    }
}my[maxn];
vector<node>ve;
int num[maxn];
int has[maxn];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n,k;
    cin>>n>>k;
    for(int i=1;i<=k;i++){
        int tot;
        cin>>tot;
        ll w;
        while(tot--){
            cin>>w;
            ve.push_back(node{i,w});
        }
    }
    sort(ve.begin(),ve.end());
    ll st=0,ans=inf;deque<node>dq;
    for(int i=0;i<ve.size();i++){
        node now=ve[i];
        dq.push_back(now);
        num[now.kind]++;
        if(num[now.kind]==1)st++;
        while(st>=k){
            node head=dq.front();
            node tail=dq.back();
            ans=min(ans,tail.x-head.x);
            dq.pop_front();
            num[head.kind]--;
            if(num[head.kind]==0)st--;
        }
    }
    cout<<ans<<endl;
    return 0;
}

P2569 [SCOI2010]股票交易(单调队列优化DP)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int n,m,ap,bp,as,bs,w,ans=0,f[2020][2020],head,tail,q[2020];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    cin>>n>>m>>w;
    memset(f,-inf,sizeof(f));
    for(int i=1;i<=n;i++){
        cin>>ap>>bp>>as>>bs;
        for(int j=0;j<=as;j++)f[i][j]=-1*j*ap;
        for(int j=0;j<=m;j++)f[i][j]=max(f[i][j],f[i-1][j]);
        if(i<=w)continue;
        head=1,tail=0;
        for(int j=0;j<=m;j++){
            while(head<=tail&&q[head]<j-as)head++;
            while(head<=tail&&f[i-w-1][q[tail]]+q[tail]*ap<f[i-w-1][j]+j*ap)tail--;
            q[++tail]=j;
            if(head<=tail)f[i][j]=max(f[i][j],f[i-w-1][q[head]]+q[head]*ap-j*ap);
        }
        head=1,tail=0;
        for(int j=m;j>=0;j--){
            while(head<=tail&&q[head]>j+bs)head++;
            while(head<=tail&&f[i-w-1][q[tail]]+q[tail]*bp<f[i-w-1][j]+j*bp)tail--;
            q[++tail]=j;
            if(head<=tail)f[i][j]=max(f[i][j],f[i-w-1][q[head]]+q[head]*bp-j*bp);

        }
    }
    for(int i=0;i<=m;i++)ans=max(ans,f[n][i]);
    cout<<ans<<endl;
    return 0;
}

luowentaoaa

嘤嘤嘤

125 posting

53 tags

A.HDU - 1520 Anniversary party

父亲结点和子结点不能同取

题意

思路

B.POJ - 1655 Balancing Act

树的重心

题意

题解

C.HDU - 2196 Computer

给出一棵树，求离每个节点最远的点的距离

题解

D.UVA - 12186 Another Crisis

为了让信息传到i，需要的最少人数

题意

题解

E.UVA - 1220 Party at Hali-Bula

G.CodeForces - 461B Appleman and Tree

每个联通块中只有一个黑色的点

题意

题解

I.CodeForces - 161D Distance in Tree

长度为K的二元组个数

J.CodeForces - 767C Garland

把一个树切成三个权值相同的树

题解

总结

C++对正则表达式的支持

运用规则

代码中运用实例如下

常用的正则表达式

检验数字的表达式

检验字符的表达式

特殊需求表达式

A.HihoCoder - 1871 Heshen’s Account Book

模板：

例题1.BZOJ3676

题意

例题2 UVA7041

题意

例题3ACM-ICPC 2018 南京赛区网络预赛 Skr

题意

例题4 HIHO#1602 : 本质不同的回文子串的数量

A华华听月月唱歌 (贪心)

B.华华教月月做数学 (快速幂+龟速乘)

C.华华给月月出题 (线性筛 极性函数)

D.月月给华华出题 (线性筛欧拉函数)

E.华华给月月准备礼物 (二分)

F.华华开始学信息学 (分类讨论+树状数组)

G.华华对月月的忠诚 (思维)

H.华华和月月种树 (树状数组)

I.华华和月月逛公园 (求桥)

J. 月月查华华的手机 (贪心)

一.网络流:流&网络&割

1.网络流问题(NetWork Flow Problem):

2.三个基本的性质:

3.容量网络&流量网络&残留网络:

4.割&割集:

二.计算最大流的基本算法

Edmonds-Karp算法 即最短路径增广算法 简称EK算法

1.最多要增广多少次?

2.如何找到一条增广路?

.如何增广?

三.最大流最小割定理

1.任意一个流都小于等于任意一个割

2.构造出一个流等于一个割

3.最大流等于最小割

最大流

增广路算法(Ford-Fulkerson)

一般增广路算法(EdmondsKarp)

算法流程

算法实现

算法复杂度

Dinic算法

算法思想

算法流程

算法实现

当前弧优化和多路增广

时间复杂度

最短增广路算法(SAP)

算法思想

C.华华给月月出题 (线性筛极性函数)

Edmonds-Karp算法即最短路径增广算法简称EK算法

树状数组套主席树（二维数点）