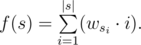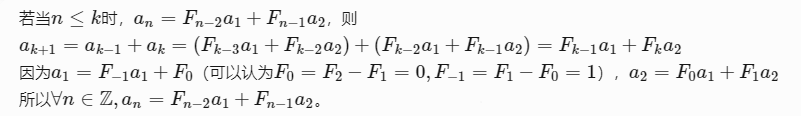Diposting di | Edited on

标准数据结构

数字

1
2
3
4
5
1、Python可以同时为多个变量赋值，如a, b = 1, 2。
2、一个变量可以通过赋值指向不同类型的对象。
3、数值的除法包含两个运算符：/ 返回一个浮点数，// 返回一个整数。
4、在混合计算时，Python会把整型转换成为浮点数。
Python还支持复数，复数由实数部分和虚数部分构成，可以用a + bj,或者complex(a,b)表示， 复数的实部a和虚部b都是浮点型

字符串

1
2
3
4
5
Python中的字符串用单引号 ' 或双引号 " 括起来
1、反斜杠可以用来转义，使用r可以让反斜杠不发生转义。
2、字符串可以用+运算符连接在一起，用*运算符重复。
3、Python中的字符串有两种索引方式，从左往右以0开始，从右往左以-1开始。
4、Python中的字符串不能改变。

List

1
2
3
4
5
6
列表是写在方括号 [] 之间、用逗号分隔开的元素列表。
1、List写在方括号之间，元素用逗号隔开。
2、和字符串一样，list可以被索引和切片。
3、List可以使用+操作符进行拼接。
4、List中的元素是可以改变的。
Python 列表截取可以接收第三个参数，参数作用是截取的步长，以下实例在索引 1 到索引 4 的位置并设置为步长为 2（间隔一个位置）来截取字符串：

Tuple（元组）

1
2
3
4
5
6
7
8
string、list 和 tuple 都属于 sequence（序列）。
元组（tuple）与列表类似，不同之处在于元组的元素不能修改。元组写在小括号 () 里，元素之间用逗号隔开。
注意：

1、与字符串一样，元组的元素不能修改。
2、元组也可以被索引和切片，方法一样。
3、注意构造包含 0 或 1 个元素的元组的特殊语法规则。
4、元组也可以使用+操作符进行拼接。

Set（集合）

1
2
3
4
5
6
7
8
9
10
11
集合（set）是由一个或数个形态各异的大小整体组成的，构成集合的事物或对象称作元素或是成员。

基本功能是进行成员关系测试和删除重复元素。

可以使用大括号 { } 或者 set() 函数创建集合，注意：创建一个空集合必须用 set() 而不是 { }，因为 { } 是用来创建一个空字典。

创建格式：

parame = {value01,value02,...}
或者
set(value)

Dictionary（字典）

1
2
3
4
5
6
7
另外，字典类型也有一些内置的函数，例如clear()、keys()、values()等。

注意：

1、字典是一种映射类型，它的元素是键值对。
2、字典的关键字必须为不可变类型，且不能重复。
3、创建空字典使用 { }。

Python数据类型转换

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61

函数	描述
int(x [,base])

将x转换为一个整数

float(x)

将x转换到一个浮点数

complex(real [,imag])

创建一个复数

str(x)

将对象 x 转换为字符串

repr(x)

将对象 x 转换为表达式字符串

eval(str)

用来计算在字符串中的有效Python表达式,并返回一个对象

tuple(s)

将序列 s 转换为一个元组

list(s)

将序列 s 转换为一个列表

set(s)

转换为可变集合

dict(d)

创建一个字典。d 必须是一个序列 (key,value)元组。

frozenset(s)

转换为不可变集合

chr(x)

将一个整数转换为一个字符

ord(x)

将一个字符转换为它的整数值

hex(x)

将一个整数转换为一个十六进制字符串

oct(x)

将一个整数转换为一个八进制字符串

Diposting di | Edited on 
1
2
3
//配置的是你个人的用户名称和电子邮件地址
$ git config --global user.name "John Doe"
$ git config --global user.email johndoe@example.com
1
2
3
4
5
6
7
8
9
10
11
12
//查已有的配置信息，可以使用 git config --list 命令
$ git config --list
user.name=Scott Chacon
user.email=schacon@gmail.com
color.status=auto
color.branch=auto
color.interactive=auto
color.diff=auto
...
//查阅某个环境变量的设定
$ git config user.name
Scott Chacon
1
2
3
4
5
//使用帮助
$ git help <verb>
$ git <verb> --help
$ man git-<verb>
$ git help config

Diposting di | Edited on

传送门

A - DZY Loves Hash （签到）

题意

给你一堆数,让你mod一个值，然后问你第一个重复的值是再第几次输入，没有重复就输出-1

思路

签到

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=1e5+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int a[maxn];
int ans=0;
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int p,n;
    cin>>p>>n;
    for(int i=1;i<=n;i++){
        int k;
        cin>>k;
        k%=p;
        if(a[k]&&!ans){
            ans++;
            a[k]++;
            cout<<i<<endl;
        }
        a[k]++;
    }
    if(!ans)cout<<-1<<endl;
    return 0;
}

B - DZY Loves Strings （结论）

题意

给你一个字符串,你可以插入K个字符,每个字符都有一个权值W

img

使得f(s)最大

思路

做过的一题

因为字符个数没有限制 所以直接无脑选最大的就行，然后就是考虑放在哪

如果把字符放前面那么原字符串的某些W值比较小的就会被推到后面使得答案变小

所以直接无脑放最后就行

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=1e5+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
ll a[maxn];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    string s;
    cin>>s;
    int k;cin>>k;
    ll mx=0;
    ll ans=0;
    for(int i=0;i<26;i++){
        cin>>a[i];
        mx=max(mx,a[i]);
    }
    int len=s.size();
    for(int i=0;i<len;i++)
        ans+=(i+1LL)*a[s[i]-'a'];
    for(int i=1;i<=k;i++){
        ans+=(len+i*1LL)*mx;
    }
    cout<<ans;
    return 0;
}

C - DZY Loves Sequences (DP)

题意

给你一个数组,你可以改变一个位置的值，让你找到一个最长的严格递增的字串

输出字串长度

思路

一开始直接DP 从头开始做了设

然后果断wa4

后面发现这样只能保证前面的答案，但是如果后面的答案更优就会导致答案错误

所以我们 直接枚举修改的位置然后判断这个修改之后前后能否连接的答案是多少

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=1e5+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
ll head[maxn];
ll tail[maxn];
ll a[maxn];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n;
    cin>>n;
    ll ans=0;
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    for(int i=1;i<=n;i++){
        head[i]=1;
        if(a[i]>a[i-1])head[i]=head[i-1]+1;
        ans=max(ans,head[i]);
        if(i<n)ans=max(ans,head[i]+1);
    }
    for(int i=n;i>=1;i--){
        tail[i]=1;
        if(a[i]<a[i+1])tail[i]=tail[i+1]+1;
        ans=max(ans,tail[i]);
        if(i>1)ans=max(ans,tail[i]+1);
    }
    for(int i=2;i<n;i++){
        if(a[i-1]<a[i+1]-1)ans=max(head[i-1]+tail[i+1]+1,ans);
    }


    cout<<ans;
    return 0;
}

D - DZY Loves Modification( 优先队列)

题意

给出一个N×M的矩阵，每次可以使得一行或者一列的所有元素减少P

然后答案加上删去P之前的行（列）的值

让你输出必须操作K次之后的最大值

思路

首先行和列直接是有关联的 不好处理

那么我们想想有没有办法分离行列之间的关系

我们发现如果我们删去任意一行 这是每一列的值都会减少P

假设我们删了q次行，那么对于后面的每一次删除列的值都会减少q×P

所以行列之间的关系找到了

假设我们删去了一列那么我们的答案为P+（删去列获得的值）-q×P

然后我们可以发现再固定删去行的次数之后 每次删去列的次数也固定了，

假设删去K次行，那么之后的答案肯定会少去{q×P×(k-q)}

那么我们就只需要使得答案没有删去之前的答案最大就行了，

那么我们直接优先队列乱搞就行

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
priority_queue<ll>prow,pcol;
ll row[maxn],col[maxn];
ll a[1200][1200];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n,m,k,p;
    cin>>n>>m>>k>>p;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cin>>a[i][j];
        }
    }
    for(int i=1;i<=n;i++){
        ll sum=0;
        for(int j=1;j<=m;j++){
            sum+=a[i][j];
        }
        prow.push(sum);
    }
    for(int i=1;i<=m;i++){
        ll sum=0;
        for(int j=1;j<=n;j++){
            sum+=a[j][i];
        }
        pcol.push(sum);
    }
    for(int i=1;i<=k;i++){
        row[i]=prow.top();
        prow.pop();
        prow.push(row[i]-1LL*m*p);
        row[i]+=row[i-1];
    }
    for(int i=1;i<=k;i++){
        col[i]=pcol.top();
        pcol.pop();
        pcol.push(col[i]-1LL*n*p);
        col[i]+=col[i-1];
    }
    ll ans=-inf;
    for(int i=0;i<=k;i++){
        ans=max(ans,row[i]+col[k-i]-1LL*(1LL*i*(k-i))*p);
    }
    cout<<ans;
    return 0;
}

E - DZY Loves Fibonacci Numbers(线段树+斐波那契数列性质)

题意

给你一个数组,你有两种操作，

1.把一个区间的值依次加上斐波那契数列的(i-start+1)项的值

2.输出一个区间的合

思路

参考

首先讨论斐波那契的性质

现在给出与本题有关的三个性质

1：若a，b满足

若

那么

2：有通项公式

3：

有前缀和公示

接下来证明时间

证明1：

证明2：

证明3：

所以我们可以记录 通过前两项的值就得出一段区间的和

通过性质1，我们知道 前两项的答案 可以叠加；
通过性质2，我们可以O(1)地将f1,f2下放；
通过性质3，我们可以O(1)地更新sum。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+9;
const int maxn=3e5+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
ll sum[maxn];
ll a[maxn];
ll fib[maxn];
struct SegTree{
    struct node{
        ll f1,f2,sum;
    }my[maxn<<4];
    #define ls (o<<1)
    #define rs (o<<1|1)
    void push_up(int o,int len){
        my[o].f1%=mod;my[o].f2%=mod;
        my[o].sum=my[ls].sum+my[rs].sum+
        ((my[o].f1*fib[len])%mod+(my[o].f2*fib[len+1]%mod)-my[o].f2+mod)%mod;
        my[o].sum%=mod;
    }
    void push_down(int o,int l,int r){
        if(!my[o].f1&&!my[o].f2)return ;
        int mid=(l+r)/2;
        my[ls].f1+=my[o].f1;
        my[rs].f1+=(my[o].f1*fib[mid-l])%mod+(my[o].f2*fib[mid-l+1])%mod;
        my[ls].f2+=my[o].f2;
        my[rs].f2+=(my[o].f1*fib[mid-l+1])%mod+(my[o].f2*fib[mid-l+2])%mod;
        my[o].f1=my[o].f2=0;
        push_up(ls,mid-l+1);
        push_up(rs,r-mid);
    }
    void ins(int o,int l,int r,int ql,int qr){
        if(ql<=l&&r<=qr){
            my[o].f1+=fib[l-ql+1];
            my[o].f1%=mod;
            my[o].f2+=fib[l-ql+2];
            my[o].f2%=mod;
            push_up(o,r-l+1);
            return;
        }
        push_down(o,l,r);
        int mid=(l+r)/2;
        if(ql<=mid)ins(ls,l,mid,ql,qr);
        if(qr>mid)ins(rs,mid+1,r,ql,qr);
        push_up(o,r-l+1);
    }
    ll query(int o,int l,int r,int ql,int qr){
        if(ql<=l&&r<=qr){
            return my[o].sum;
        }
        push_down(o,l,r);
        int mid=(l+r)/2;
        ll ans=0;
        if(ql<=mid)ans+=query(ls,l,mid,ql,qr);
        if(qr>mid)ans+=query(rs,mid+1,r,ql,qr);
        ans%=mod;
        return ans;
    }
}seg;
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n,m;
    cin>>n>>m;
    fib[1]=fib[2]=1;
    for(int i=3;i<=n+3;i++)fib[i]=(fib[i-1]+fib[i-2])%mod;
    for(int i=1;i<=n;i++)cin>>a[i],sum[i]=(sum[i-1]+a[i])%mod;
    while(m--){
        int op,l,r;
        cin>>op>>l>>r;
        if(op==1)seg.ins(1,1,n,l,r);
        else cout<<(seg.query(1,1,n,l,r)+(sum[r]-sum[l-1])%mod+mod)%mod<<endl;
    }
    return 0;
}

Diposting di | Edited on

传送门

A.Middle of the Contest （签到）

题意

求两个时间的中间时刻

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e8+7;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
typedef unsigned long long ull;

int main()
{
    /*std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);*/
    int h1,h2,m1,m2;
    string s;
    cin>>s;
    h1=(s[0]-'0')*10+s[1]-'0';
    m1=(s[3]-'0')*10+s[4]-'0';
    cin>>s;
    h2=(s[0]-'0')*10+s[1]-'0';
    m2=(s[3]-'0')*10+s[4]-'0';
    int h3=h1*60+m1;
    int m3=h2*60+m2;
    int num=(h3+m3)/2;
    printf("%02d:%02d\n",num/60,num%60);
    return 0;
}

B - Preparation for International Women’s Day (水)

题意

求有多少个数可以组合成K的倍数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e8+7;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
typedef unsigned long long ull;
int low[150];
int high[150];
int flag[150];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n,k;
    cin>>n>>k;
    for(int i=1;i<=n;i++){
        int a;cin>>a;
        high[a%k]++;
    }
    int ans=high[0]/2;
    for(int i=1;i<k/2;i++)ans+=min(high[i],high[k-i]);
    if(k%2==0)ans+=high[k/2]/2;
    else ans+=min(high[k/2],high[k/2+1]);
    cout<<ans*2<<endl;
    return 0;
}

C - Balanced Team (单调队列)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e8+7;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
typedef unsigned long long ull;
int a[maxn];

int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n,k;
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    deque<int>dq;
    sort(a+1,a+1+n);
    int ans=0;
    for(int i=1;i<=n;i++){
        dq.push_back(a[i]);
        while(!dq.empty()&&dq.front()+5<dq.back())dq.pop_front();
        ans=max(ans,(int)dq.size());
    }
    cout<<ans<<endl;
    return 0;
}

D - Zero Quantity Maximization (map)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e8+7;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
typedef unsigned long long ull;
ll a[maxn],b[maxn];
map<pair<ll,ll>,int>mp;
int ans=0;
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n;
    cin>>n;
    int zero=0;
    for(int i=1;i<=n;i++)cin>>a[i];
    for(int j=1;j<=n;j++)cin>>b[j];
    for(int i=1;i<=n;i++){
        if(a[i]==0&&b[i]==0){
            zero++;
            continue;
        }
        if(a[i]==0)continue;
        ll q=__gcd(abs(a[i]),abs(b[i]));
        a[i]/=q;
        b[i]/=q;
        if(a[i]<0)b[i]=-b[i],a[i]=-a[i];
        mp[{a[i],b[i]}]++;
        ans=max(ans,mp[{a[i],b[i]}]);
    }
    cout<<ans+zero;
    return 0;
}

E - K Balanced Teams (DP)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e8+7;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
typedef unsigned long long ull;
int dp[5500][5500],a[maxn],b[maxn];
deque<int>dq;
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n,k,ans=0;
    cin>>n>>k;
    for(int i=1;i<=n;i++)cin>>a[i];
    sort(a+1,a+1+n);
    for(int i=1;i<=n;i++){
        dq.push_back(a[i]);
        while(!dq.empty()&&dq.front()+5<dq.back())dq.pop_front();
        b[i]=dq.size();
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=k;j++){
            dp[i][j]=max(dp[i-1][j],dp[i][j]);
            dp[i][j]=max(dp[i][j],dp[i-b[i]][j-1]+b[i]);
            ans=max(dp[i][j],ans);
        }
    }
    cout<<ans;
    return 0;
}

F1 - Spanning Tree with Maximum Degree (MST)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e8+7;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
typedef unsigned long long ull;
vector<int>G[maxn];
int a[maxn],b[maxn],fa[maxn],d[maxn];
int find(int x){
    return x==fa[x]?fa[x]:fa[x]=find(fa[x]);
}
void fix(int u,int v){
    int fu=find(u);
    int fv=find(v);
    if(fv==fu)return;
    fa[fu]=fv;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n,m,mx=0,rt;
    cin>>n>>m;
    for(int i=1;i<=n;i++)fa[i]=i;
    for(int i=1;i<=m;i++){
        cin>>a[i]>>b[i];
        d[a[i]]++;d[b[i]]++;
        if(d[a[i]]>mx)mx=d[a[i]],rt=a[i];
        if(d[b[i]]>mx)mx=d[b[i]],rt=b[i];
        G[a[i]].push_back(b[i]);
        G[b[i]].push_back(a[i]);
    }
    for(int i=0;i<G[rt].size();i++){
        cout<<rt<<" "<<G[rt][i]<<endl;
        fix(rt,G[rt][i]);
    }
    for(int i=1;i<=m;i++){
        int aa=find(a[i]),bb=find(b[i]);
        if(aa==bb)continue;
        cout<<a[i]<<" "<<b[i]<<endl;
        fix(a[i],b[i]);
    }
    return 0;
}

F2 - Spanning Tree with One Fixed Degree (构造)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e8+7;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
typedef unsigned long long ull;
vector<int>G[maxn];
int a[maxn],b[maxn],fa[maxn],d[maxn];
int find(int x){
    return x==fa[x]?fa[x]:fa[x]=find(fa[x]);
}
void fix(int u,int v){
    int fu=find(u);
    int fv=find(v);
    if(fv==fu)return;
    fa[fu]=fv;
}
bool flag[maxn];

int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n,m,k;
    cin>>n>>m>>k;
    for(int i=1;i<=n;i++)fa[i]=i;
    int cnt=0;
    for(int i=1;i<=m;i++){
        cin>>a[i]>>b[i];
        G[a[i]].push_back(b[i]);
        G[b[i]].push_back(a[i]);
        if(a[i]!=1&&b[i]!=1&&(find(a[i])!=find(b[i])))fix(a[i],b[i]),cnt++;
    }
    for(int i=1;i<=m;i++){
        if(a[i]==1||b[i]==1){
            int aa=find(a[i]);
            int bb=find(b[i]);
            if((aa!=bb)&&k){
                fix(a[i],b[i]);
                k--;cnt++;
                flag[i]=1;
            }
        }
    }
    for(int i=1;i<=m;i++){
        if(a[i]==1||b[i]==1){
            int aa=find(a[i]);
            int bb=find(b[i]);
            if(aa==bb&&flag[i]==0&&k){
                k--;
                flag[i]=1;
            }
        }
    }
    if(k||cnt!=n-1)cout<<"NO"<<endl,exit(0);
    cout<<"YES"<<endl;
    for(int i=1;i<=n;i++)fa[i]=i;
    for(int i=1;i<=m;i++){
        if(flag[i]){
            fix(a[i],b[i]);
            cout<<a[i]<<" "<<b[i]<<endl;
        }
    }
    for(int i=1;i<=m;i++){
        if(a[i]!=1&&b[i]!=1){
            if(find(a[i])!=find(b[i])){
                fix(a[i],b[i]);
                cout<<a[i]<<" "<<b[i]<<endl;
            }
        }
    }

    return 0;
}

Diposting di | Edited on

传送门

C.Captain Marmot (几何,点旋转)

思路

其中顺时针旋转为负，逆时针旋转为正，角度angle是弧度值，如旋转30度转换为弧度为： $angle = pi/180 * 30$。

4、度与角度的转换
根据圆为$360 º​$，弧度为$2π​$，即 $360º = 2π​$

4.1 角度转弧度：$2π / 360 = π / 180 ≈ 0.0174rad$, 即: $度数 (π / 180） = 弧度$
例如：将30º转为弧度rad
$ 30º (π / 180）= 0.523320 rad $

4.2 弧度转角度: $360 / 2π = 180 / π ≈ 57.3º$, 即: $ 弧度 (180 / π） = 度数$
例如：将$0.523320rad$转为度º
$0.523320rad (180 / π) = 29.9992352688º ​$

若o不是原点，则可先将a点坐标转换为相对坐标计算，计算结果再加上o点坐标。

参与计算的a点坐标实际应为 a - 0,最终计算公式如下：

$b.x = ( a.x - o.x)cos(angle) - (a.y - o.y)sin(angle) + o.x​$

$b.y = (a.x - o.x)sin(angle) + (a.y - o.y)cos(angle) + o.y$

Flowers (DP)

思路

少于k的肯定全是1因为都只能放红色。

大于K的可以放红色$dp[i-1]$ 或者连续的k个白色$dp[i-k]$

Diposting di | Edited on

传送门

A - George and Accommodation(签到)

思路

B - Fedor and New Game(暴力)

C - George and Job (基础DP)

思路

很明显$k$组的答案从$k-1$组得来，而且第$i$个位置的答案只能从$i-m$的位置以及之前转移过来

很明显,维护一个$num$数组储存$i-m$及其之前的各组答案的最大值即可

D - Fedor and Essay (建图spfa)

思路

根据长度和K的数量作为权值，根据关心建图，然后跑一个bfs(spfa)

[E - Alex and Complicated Task]https://codeforces.com/contest/467/problem/E) (贪心)

思路

因为题目限制，所以我们可以用个栈和map维护第三个数和第二个数的前后位置

Diposting di | Edited on

传送门

[A - inc ARG(签到)

题意

给你一个二进制数，问你加1之后有多少位会变化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include<bits/stdc++.h>
using namespace std;

int main(){
    int n;
    string s;
    cin>>n>>s;
    int num=0;
    for(int i=0;i<s.size();i++){
        if(s[i]=='1')num++;
        else break;
    }
    cout<<min(num+1,n)<<endl;
}

B - Inbox (100500) （水）

题意

一个电子邮箱，两种状态一种目录状态可以去在这里去任意一个信件，一种是浏览模式可以进到信件里面，如果这个信件是未读的就会变成已读，在浏览模式里面可以选择进入下一份相邻信件的浏览模式。每次点击可以进入目录模式or浏览模式or进入下一个相邻信件

问你最少多少次可以吧所有信件变成已读

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include<bits/stdc++.h>
using namespace std;
const int maxn=1300;
int a[maxn];
int main(){

    int n,num=0;
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    int first=0;
    for(int i=1;i<=n;i++){
        if((a[i]==1&&a[i-1]==1)||(!first&&a[i]==1))num++,first=1;
        else if(a[i]==1&&a[i-1]==0)num+=2;
    }
    cout<<num<<endl;
    return 0;
}

C - No to Palindromes! (暴力模拟)

题意

给你一个不是回文的字符串，只能用不超过‘K的字符。问你这个字符串还大的字典序并且不是回文的字符串是什么

思路

首先如果改变的那一位的相邻两位不一样和隔一位不一样就不可能有回文

直接从后面暴力枚举状态

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include<bits/stdc++.h>
using namespace std;
const int maxn=1300;

char s[maxn];
int n,p;
bool check(int pos){
    if(pos>=1){
        if(s[pos]==s[pos-1])return false;
    }
    if(pos>=2){
        if(s[pos]==s[pos-2])return false;
    }
    return true;
}
int main(){
    cin>>n>>p;
    cin>>s;
    int pos=n-1;
    while(true){
       // cout<<"pos="<<pos<<endl;
       // cout<<"s="<<s<<endl;
        if(pos==n)cout<<s<<endl,exit(0);
        if(pos==-1)cout<<"NO"<<endl,exit(0);
        if(s[pos]-'a'+1==p){
            s[pos]='a'-1;pos--;
            continue;
        }
        else{
            s[pos]=(s[pos]-'a'+1)%p+'a';
            if(check(pos)){
                pos++;
            }
        }

    }
    return 0;
}

D - Restore Cube (模拟，深搜)

题意

给你一个八面体，八面体的每个顶点的坐标x,y,z被打乱了，问你是否原来的是一个正方体

思路

直接暴力枚举复杂度是6^8 然后判断是否符合正方体的性质即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1300;
vector<ll>v[8];
ll get(int x){
    return 1LL*x*x;
}
ll dist(vector<ll> a,vector<ll> b){
    return get(a[0]-b[0])+get(a[1]-b[1])+get(a[2]-b[2]);
}
void prin(vector<ll> a){
    for(int i=0;i<a.size();i++)cout<<a[i]<<" ";
    cout<<endl;
}
bool diff(){
    for(int i=0;i<8;i++){
        for(int j=i+1;j<8;j++){
            if(v[i]==v[j])return true;
        }
    }
    return false;
}
void dfs(int id,set<ll> a){
    if(a.size()>3)return ;
    if(id==8){
        if(a.size()==3){
            cout<<"YES"<<endl;
            for(int i=0;i<8;i++)prin(v[i]);
            exit(0);
        }
        return;
    }
    do{
        set<ll>now=a;
        for(int i=0;i<id;i++)now.insert(dist(v[i],v[id]));
        dfs(id+1,now);
    }while(next_permutation(v[id].begin(),v[id].end()));
}

int main(){
    for(int i=0;i<8;i++){
        for(int j=0;j<3;j++){
            ll a;cin>>a;
            v[i].push_back(a);
        }
        sort(v[i].begin(),v[i].end());
    }
    set<ll>s;
    dfs(0,s);
    cout<<"NO"<<endl;
    return 0;
}

E - Substitutes in Number (模拟 费马小定理)

题意

给出一个数字字符串，每次操作把一个数字替换成一个数字字符串，

之后把整个数字字符串变成十进制输出

思路

暴力肯定爆炸字符串长度是指数上升的。

一开始 要获得字符串中一个数字的价值是 原值*10+val 所以原本一个数字的贡献是 其中的$\times$ 和val 发现替换也就是在替换这个val和$\times$

我们从后模拟被替换的字符串的价值和$\times$ 就行了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e5+50;
const ll mod=1e9+7;
#define bug cout<<"hello"<<endl;
int n;
ll ksm(ll a,ll b){
    ll ans=1;
    while(b){
        if(b&1)ans=(ans*a)%mod;
        a=(a*a)%mod;
        b>>=1;
    }
    return ans;
}
ll val[20],len[20];
struct node{
    string s;
    int id;
    vector<int>v;
    void build(){
        id=s[0]-'0';
        for(int i=3;i<s.size();i++){
            v.push_back(s[i]-'0');
        }
    }
    void update(){
        ll l=0,va=0;
        for(int i=0;i<v.size();i++){
            l+=len[v[i]];
            va*=ksm(10LL,len[v[i]]);
            va%=mod;
            va+=val[v[i]];
            va%=mod;
            l%=mod-1;
        }
        val[id]=va;len[id]=l;
    }
}my[maxn];
string str;
int main(){
    for(int i=0;i<10;i++)val[i]=i,len[i]=1;
    cin>>str;
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>my[i].s;
        my[i].build();
    }

    for(int i=n;i;i--){
        my[i].update();
    }
    ll ans=0;
    for(int i=0;i<str.size();i++){
        ans*=ksm(10,len[str[i]-'0']);
        ans%=mod;
        ans+=val[str[i]-'0'];
        ans%=mod;
    }
    cout<<ans<<endl;
    return 0;
}

Diposting di | Edited on

传送门

A - Appleman and Easy Task （签到）

题意

判断棋盘中是否每个点四周都有偶数个‘x’

思路

暴力

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=2e6+50;
const ll inf=1e17;
typedef unsigned long long ull;

char s[150][150];
int dx[4]={1,-1,0,0};
int dy[4]={0,0,1,-1};
int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>s[i]+1;
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            int cnt=0;
            for(int k=0;k<4;k++){
                int xx=i+dx[k];
                int yy=j+dy[k];
                cnt+=s[xx][yy]=='o';
            }
            if(cnt&1)puts("NO"),exit(0);
        }
    }
    puts("YES");
    return 0;
}

B - Appleman and Card Game (贪心)

题意

可以选K个字母，价值是这个字母的数量的平方，求最大的价值

思路

平方函数斜率得知 x越大价值越大

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=2e6+50;
const ll inf=1e17;
typedef unsigned long long ull;

char s[maxn];
int num[maxn];
int main()
{
    int n,k;
    cin>>n>>k;
    cin>>s;
    int len=strlen(s);
    ll ans=0;
    for(int i=0;i<len;i++)num[s[i]-'A']++;
    sort(num,num+26,greater<int>());
    for(int i=0;i<26;i++){
        if(num[i]){
            if(k>=num[i])k-=num[i],ans+=1LL*num[i]*num[i];
            else{
                ans+=1LL*k*k;k=0;
            }
        }
    }
    cout<<ans<<endl;
    return 0;
}

C - Appleman and Toastman (贪心)

题意

AB做一个游戏，A给B一个数组，B把数组切一刀 然后再给A，如果B收到一个单独的数字就把这个数字扔掉，如果A收到一组数价值就加这组数字和

思路

贪心得每次让B把数组的最小的切掉

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=2e6+50;
const ll inf=1e17;
typedef unsigned long long ull;

ll a[maxn];

int main()
{
    int n,k;
    cin>>n;
    ll sum=0;
    priority_queue<ll,vector<ll>,greater<int> >Q;
    for(int i=1;i<=n;i++)cin>>a[i],sum+=a[i],Q.push(a[i]);
    sort(a+1,a+1+n);
    ll ans=0;
    while(!Q.empty()){
        ans+=sum;
        if(Q.size()>1)
            ans+=Q.top();
        sum-=Q.top();
        Q.pop();
    }
    cout<<ans<<endl;
    return 0;
}

D - Appleman and Tree (树形DP)

题意

给出一棵以0为根的树,每个节点都有可能是黑色或者白色，让你分成K部分，使得每部分都恰好有一个黑点 求方案数

思路

考虑只有两个相邻结点，A，B

如果A所在部分想要是黑色，那么他就要么自己是黑色，那就需要把B是黑色的切掉

如果A所在部分想要是黑色，那么他就要么自己是黑色，那就需要把B是白色的连接

如果A所在部分想要是黑色，那么他就要么自己是白色，那就需要把B是黑色的连接

如果A所在部分想要是白色，他们他自己只能是白色，那就需要把B是黑色的切掉

如果A所在部分想要是白色，他们他自己只能是白色，那就需要把B是白色的相连

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=2e5+50;
const ll inf=1e17;
typedef unsigned long long ull;

vector<int>G[maxn];
int val[maxn];
ll dp[maxn][2];

void dfs(int u){
    if(val[u])dp[u][1]=1,dp[u][0]=0;
    else dp[u][0]=1,dp[u][1]=0;
    for(int i=0;i<G[u].size();i++){
        int now=G[u][i];
        dfs(now);
        ll yes=dp[u][1];
        ll no=dp[u][0];
        dp[u][1]=1LL*yes*dp[now][1]%mod;
        dp[u][1]+=1LL*yes*dp[now][0]%mod;
        dp[u][1]+=1LL*no*dp[now][1]%mod;
        dp[u][0]=1LL*no*dp[now][1]%mod;
        dp[u][0]+=1LL*no*dp[now][0]%mod;
        dp[u][1]%=mod;
        dp[u][0]%=mod;
        /*cout<<"dp[now][1]="<<dp[now][1]<<" dp[now][0]="<<dp[now][0]<<endl;
        cout<<"dp[u][1]="<<dp[u][1]<<" dp[u][0]="<<dp[u][0]<<endl;
        cout<<"yes="<<yes<<" no="<<no<<endl;*/
    }
}

int main()
{
    int n;
    cin>>n;

    for(int i=1;i<n;i++){
        int x;
        cin>>x;
        G[x].push_back(i);
    }
    for(int i=0;i<n;i++){
        cin>>val[i];
    }
    dfs(0);
    cout<<dp[0][1]<<endl;

    return 0;
}

E - Appleman and a Sheet of Paper（树状数组大模拟）

题意

给你一张纸 参考1*n的数组

然后两种操作，给你一个K，让你把左边K个数组折到右边

第二个操作 询问区间范围内的纸张厚度和

思路

因为每个操作1都会让至少一个格子变少，所以直接暴力即可

然后区间求和就可以用数据结构维护

发现操作1可能K比后面的长度还大，这时候就可以倒过来，相当于让后面N-K个折到左边

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=1e5+50;
const int inf=1e8;

typedef unsigned long long ull;
int n,q;
int a[maxn];
bool pre;
void update(int x,int y){
    while(x<=n)a[x]+=y,x+=x&-x;
}
int sum(int x){
    int ans=0;
    while(x){
        ans+=a[x];x-=x&-x;
    }
    return ans;
}
int get(int l,int r){
    if(l>r)swap(l,r);
    return sum(r)-sum(l);
}
int main()
{
    cin>>n>>q;
    for(int i=1;i<=n;i++)update(i,1);
    int cl=1,cr=n;
    while(q--){
        int t,l,r;
        cin>>t;
        if(t==1){
            int sz=cr-cl+1;
            cin>>l;
            if(l>sz/2){
                pre=!pre;
                l=sz-l;
            }
            if(pre){
                for(int j=0;j<l;j++)
                    update(cr-l-j,get(cr-l+j,cr-l+j+1));
                cr-=l;
            }
            else{
                for(int j=0;j<l;j++)
                    update(cl+l+j,get(cl+l-j-1,cl+l-j-2));
                cl+=l;
            }
        }
        else{
            cin>>l>>r;
            l++;
            if(pre)cout<<get(cr-r,cr-l+1)<<endl;
            else cout<<get(cl+l-2,cl+r-1)<<endl;
        }
    }
    return 0;
}

Diposting di | Edited on

传送门

A - Pashmak and Garden （签到）

题意

对于一个正方形给你其中两个点，让你输出另外两个点

思路

水

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=1e5+50;
const int inf=1e9;
typedef unsigned long long ull;

int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int x1,x2,y1,y2;
    cin>>x1>>y1>>x2>>y2;

    if(x1==x2){
        int dis=abs(y1-y2);
        cout<<x1+dis<<" "<<y1<<" ";
        cout<<x2+dis<<" "<<y2<<endl;
    }
    else if(y1==y2){
        int dis=abs(x1-x2);
        cout<<x1<<" "<<y1+dis<<" ";
        cout<<x2<<" "<<y2+dis<<endl;
    }
    else{
        int dis1=abs(x1-x2);
        int dis2=abs(y1-y2);
        if(dis1!=dis2)puts("-1");
        else{
            cout<<x2<<" "<<y1<<" ";
            cout<<x1<<" "<<y2<<endl;
        }
    }
    return 0;
}

B - Pashmak and Flowers （水题）

题意

一堆数，找出两个数使得差值最大，输出这两个数有多少种选择

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=2e5+50;
const int inf=1e9;
typedef unsigned long long ull;
int a[maxn];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n;
    cin>>n;
    int mx=-(1e9+7),mi=1e9+7;
    int aa=0,bb=0;
    for(int i=1;i<=n;i++){
        cin>>a[i];
        mx=max(mx,a[i]);
        mi=min(mi,a[i]);
    }
    for(int i=1;i<=n;i++){
        if(a[i]==mx)aa++;
        if(a[i]==mi)bb++;
    }
    cout<<abs(mx-mi)<<" "<<(ll)(mx==mi?1LL*aa*(aa-1)/2LL*1LL:1LL*aa*bb)<<endl;
    return 0;
}

C - Pashmak and Buses (dfs 暴力)

题意

n个人m天k个车每个人每天都要坐车，要不能出现任意两个人m天做的车都一样

思路

相当于不能有两个长度为m的字符串完全相同

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include<iostream>
#include<algorithm>
#include<string>
#include<queue>
#include<cstring>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=2e5+50;
const int inf=1e9;
typedef unsigned long long ull;
ll n,d,k;
int a[1100][1100];
int now[1100];
int cnt;
void dfs(int pos){
    if(pos==d+1){
        cnt++;
        for(int i=1;i<=d;i++)a[i][cnt]=now[i];
        return;
    }
    for(int i=1;i<=k;i++){
        now[pos]=i;
        dfs(pos+1);
        if(cnt>=n)return;
    }
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    cin>>n>>k>>d;
    int kk=1;
    bool flag=false;
    for(int i=1;i<=d;i++){
        kk*=k;
        if(kk>=n){flag=1;break;}
    }
    if(!flag)puts("-1"),exit(0);
    dfs(1);
    for(int i=1;i<=d;i++){
        for(int j=1;j<=n;j++)
            cout<<a[i][j]<<" ";
        cout<<endl;
    }

    return 0;
}

D - Pashmak and Parmida’s problem (树状数组)

题意

定义

求有多少对

思路

直接维护从后向前的值，然后从前往后遍历 查找后面小于它的值

树状数组维护

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include<iostream>
#include<algorithm>
#include<string>
#include<queue>
#include<cstring>
#include<unordered_map>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=2e6+50;
const int inf=1e9;
typedef unsigned long long ull;
int a[maxn];
int c[maxn];
int lowbit(int x){
    return x&(-x);
}
int add(int x,int value){
    for(;x<maxn;x+=lowbit(x))c[x]+=value;
}
int query(int x){
    int ans=0;
    for(;x;x-=lowbit(x))ans+=c[x];
    return ans;
}
unordered_map<int,int>pre,suf;
ll ans;
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n;
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    for(int i=n;i;i--){
        suf[a[i]]++;
        add(suf[a[i]],1);
    }
    for(int i=1;i<=n;i++){
        pre[a[i]]++;
        add(suf[a[i]],-1);
        suf[a[i]]--;
        ans+=1LL*query(pre[a[i]]-1);
    }
    cout<<ans<<endl;
    return 0;
}

E - Pashmak and Graph (dp)

题意

给出一个有向图找出一个最长不简单路使得路径长度严格递增

思路

模拟一维做法，排序一个边，然后注意一下相等的情况

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=3e5+50;
const int inf=1e9;
typedef unsigned long long ull;
struct node{
    int u,v,w;
    bool operator<(const node &a)const{
        return w<a.w;
    }
}my[maxn];
int d[maxn];
int dp[maxn];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);

    int n,m;
    cin>>n>>m;
    for(int i=1;i<=m;i++){
        cin>>my[i].u>>my[i].v>>my[i].w;
    }
    sort(my+1,my+1+m);
    for(int i=1;i<=m;i++){
        int u=my[i].u;
        int v=my[i].v;
        int w=my[i].w;
        int j=i+1;
        while(j<=m&&my[j].w==w)j++;
        stack<int>st;
        for(int k=i;k<j;k++){
            d[my[k].v]=max(d[my[k].v],dp[my[k].u]+1);
            st.push(my[k].v);
        }
        while(!st.empty()){
            int now=st.top();st.pop();
            dp[now]=max(dp[now],d[now]);
            d[now]=0;
        }
        i=j-1;
    }
    cout<<*max_element(dp+1,dp+1+n)<<endl;
    return 0;
}

Diposting di | Edited on

传送门

A - Laptops (签到)

题意

给你一堆笔记本的价钱和质量问是否有电脑的价格比另一个电脑的价格低的同时质量还更好

价格和质量都小于等于笔记本数量

思路

很棒很有趣的题

一开始我想用树状数组，但是转念一想不对啊这特么才div2A

然后发现价格和质量都小于等于笔记本数量

说明只要有电脑的价格质量不一样那么就肯定会有冲突

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=2e5+50;
const int inf=1e9;
typedef unsigned long long ull;

int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n;
    cin>>n;
    bool flag=false;
    for(int i=1;i<=n;i++){
        int a,b;
        cin>>a>>b;
        if(a!=b)flag=1;
    }
    if(flag)cout<<"Happy Alex"<<endl;
    else cout<<"Poor Alex"<<endl;
    return 0;
}

B - Fedya and Maths (欧拉函数 or 打表)

题意

计算

n小于等于10的一百万次方

思路

发现直接算很蠢，然后我当时是直接打表计算。因为模数是5所以肯定会有长度最大为5的循环节

or

用欧拉降幂

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=2e5+50;
const int inf=1e9;
typedef unsigned long long ull;
int one[5]={1,1,1,1};
int two[5]={1,2,4,3};
int three[5]={1,3,4,2};
int four[5]={1,4,1,4};
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    string s;
    cin>>s;
    int len=s.size();
    int ans=0;
    for(int i=0;i<len;i++){
        ans=(ans*10+s[i]-'0')%4;
    }
    ans=(one[ans]+two[ans]+three[ans]+four[ans])%5;
    cout<<ans<<endl;
    return 0;
}

C - Boredom (DP)

题意

给出一个堆数 每次取一个a，然后把所有a-1,a+1的数全部移除，之后答案ans+a

求最大的ans

思路

因为顺序没有关系所以我们不考虑顺序

只需要考虑数的数量，

对于一个数他只被他前一个数和他后一个数影响

所以我们设DP[i]为取了前面(1-i)的最大答案值

这个数去不去只被前一个数影响，

所以如果取这个数 那么就不能取前一个数所以

如果不取这个数，那么答案就直接变成前一个的值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=2e5+50;
const int inf=1e9;
typedef unsigned long long ull;
ll dp[maxn];
ll a[maxn];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n;
    cin>>n;
    for(int i=1;i<=n;i++){
        int aa;
        cin>>aa;
        a[aa]+=aa;
    }
    dp[1]=a[1];
    ll ans=0;
    for(int i=2;i<maxn;i++){
        dp[i]=max(dp[i-1],dp[i-2]+a[i]);
        ans=max(ans,dp[i]);
    }
    cout<<ans;
    return 0;
}

B - A Lot of Games (字典树+博弈)

题意

给出N个字符串集,

开始字符串为空

两个人游戏，每次的游戏者给字符串加上一个字符 同时保证当前字符串是字符串集合其中一个字符串的前缀

游戏进行K轮，一轮游戏输者变成下一轮游戏的先手

赢了最后一轮游戏的才是最后的赢家

问你是否第一轮的先手有必胜把握

思路

首先把题目化简，变成求一轮游戏的是否能先手胜，

很明显如果一轮游戏先手必赢那么他下一轮比赛就不一定能赢了

如果一轮先手没有必赢的把握那么他比会被对面控制，也就不可能赢

是不是缺少了点啥，对，我们还需要求有没有办法让先手必输的情况；

如果先手可以把握输赢那他就能在他最后一轮先手并且赢 同时可以看出第一轮先手必赢的时候只有奇数轮才可能必赢

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=2e5+50;
const int inf=1e9;
typedef unsigned long long ull;
int tree[maxn][30];
int cnt=0;
bool iswin(int id){
    for(int i=0;i<26;i++){
        if(tree[id][i]!=-1){
            if(!iswin(tree[id][i]))return true;
        }
    }
    return false;
}
bool isfail(int id){
    bool fail=true;
    for(int i=0;i<26;i++){
        if(tree[id][i]!=-1){
            fail=false;
            if(!isfail(tree[id][i]))return true;
        }
    }
    return fail;
}
char str[maxn];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n,k;
    cin>>n>>k;
    memset(tree,-1,sizeof(tree));

    for(int i=1;i<=n;i++){
        cin>>str;
        int len=strlen(str);
        int root=0;
        for(int j=0;j<len;j++){
            root=tree[root][str[j]-'a']==-1?tree[root][str[j]-'a']=++cnt:tree[root][str[j]-'a'];
        }
    }
    bool win=iswin(0),fail=isfail(0);
    if(win){
        if(fail)cout<<"First"<<endl;
        else{
            if(k&1){
                cout<<"First"<<endl;
            }
            else cout<<"Second"<<endl;
        }
    }
    else cout<<"Second"<<endl;
    return 0;
}

C - Civilization (树直径+并查集)

题意

给你一个森林

有两种操作

1：求出一个森林中一个树的直径

2：连接两个联通块 使得树的直径最小

思路

求直径已经是模板题了，两次dfs即可

然后保证树的直径最小也是有策略的，直径要么是其中一个树的直径要么是两个树的直径的中心连接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=1e6+50;
const int inf=1e9;
typedef unsigned long long ull;
int fa[maxn];

vector<int>G[maxn];
ll ans[maxn];

int find(int x){
    return x==fa[x]?x:fa[x]=find(fa[x]);
}

void dfs(int now,int pre,int len,int &p,int &dis){
    if(len>dis){
        dis=len;
        p=now;
    }
    for(int i=0;i<G[now].size();i++){
        if(G[now][i]==pre)continue;
        dfs(G[now][i],now,len+1,p,dis);
    }
}

int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n,m,q;
    cin>>n>>m>>q;
    for(int i=1;i<=n;i++)fa[i]=i;
    for(int i=1;i<=m;i++){
        int a,b;
        cin>>a>>b;
        G[a].push_back(b);
        G[b].push_back(a);
        int aa=find(a),bb=find(b);
        if(aa!=bb){
            fa[bb]=aa;
        }
    }
    for(int i=1;i<=n;i++){
        if(fa[i]==i){
            int to=-1,dis=-1;
            dfs(i,-1,0,to,dis);
            dis=0;
            dfs(to,-1,0,to,dis);
            ans[i]=dis;
        }
    }
    while(q--){
        int op,x,y;
        cin>>op;
        if(op==1){
            cin>>x;
            x=find(x);
            cout<<ans[x]<<endl;
        }
        else{
            cin>>x>>y;
            int aa=find(x);
            int bb=find(y);
            if(aa==bb){
                continue;
            }
            else{
                fa[bb]=aa;
                ans[aa]=max((ans[aa]+1)/2+(ans[bb]+1)/2+1,max(ans[aa],ans[bb]));
            }
        }
    }
    return 0;
}

D - Serega and Fun (分块)

题意

给出一个数组，有两种操作

1：把一个区间循环右移一个数

2：查询一个区间值为K的个数

强制在线

思路

头插尾插第一想到deque

然后分块得出使得两个操作都可以sqrt(n)时间内完成

ps:发现分块新技能，block=pow(n,0.618)黄金分割线比sqrt（n)块了一倍

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=1e5+50;
const int inf=1e9;
typedef unsigned long long ull;
int block;
deque<int>dq[100];
int num[100][maxn];
int n,ans;

void update(){
    int l,r;
    cin>>l>>r;
    l=(ans+l-1)%n;r=(ans+r-1)%n;
    if(l>=r)swap(l,r);
    int a=l/block,b=r/block,aa=l%block,bb=r%block;
    int k=dq[b][bb];
    dq[b].erase(dq[b].begin()+bb);
    num[b][k]--;
    num[a][k]++;
    for(int i=a;i<b;i++){
        int now=dq[i].back();
        dq[i].pop_back();
        dq[i+1].push_front(now);
        num[i][now]--;
        num[i+1][now]++;
    }
    dq[a].insert(dq[a].begin()+aa,k);
}

void query(){
    int l,r,k;
    cin>>l>>r>>k;
    l=(ans+l-1)%n;r=(ans+r-1)%n;k=(ans+k-1)%n+1;
    if(l>=r)swap(l,r);
    ans=0;
    int a=l/block,b=r/block,aa=l%block,bb=r%block;
    if(a==b){
        for(int i=aa;i<=bb;i++){
            ans+=(dq[a][i]==k);
        }
    }
    else{
        for(int i=aa;i<dq[a].size();i++){
            ans+=(dq[a][i]==k);
        }
        for(int i=a+1;i<b;i++){
            ans+=num[i][k];
        }
        for(int i=0;i<=bb;i++){
            ans+=(dq[b][i]==k);
        }
    }
    cout<<ans<<endl;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);

    cin>>n;block=pow(n,0.618);
    for(int i=0;i<n;i++){
        int a;
        cin>>a;
        dq[i/block].push_back(a);
        num[i/block][a]++;
    }

    int m;
    cin>>m;
    while(m--){
        int op;
        cin>>op;
        if(op==1)update();
        else query();
    }

    return 0;
}
/*
7
6 6 2 7 4 2 5
7
1 3 6
2 2 4 2
*/