Diposting di | Edited on

传送门

A.The Child and Homework (签到题)

题意

给出四个字符串A,B,C,D，让你按照其中如下规则输出答案

1:如果有一个字符串的长度小于其他字符串的长度至少两倍 输出他的序号

2.如果有一个字符串的长度大于其他字符串的长度至少两倍 输出他的序号

3.如果都不符合输出C

思路

一开始直接做了，发现果断wa 发现如下坑

1.是必须要一直有一个字符串满足如上属性，如果有两个字符串满足 比如长度分别为( 1 ,2 , 4 , 8 )这里有多个符合条件 所有需要输出C；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;

int num[1500];
int cnt[1500];
int tnc[1500];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    string a;
    bool doul=false;
    for(int i=1;i<=4;i++){
        cin>>a;
        num[i]=a.length()-2;
        cnt[num[i]]++;
        tnc[num[i]]++;
    }
    for(int i=1;i<=1000;i++){
        cnt[i]+=cnt[i-1];
    }
    for(int i=1000;i>=1;i--){
        tnc[i]+=tnc[i+1];
    }
    int id=0,nu=0;
    for(int i=1;i<=4;i++){
        if(tnc[num[i]*2]>=3||cnt[num[i]/2]>=3){
            id=i;nu++;
        }
    }
    if(nu!=1)
        cout<<"C"<<endl;
    else{
        cout<<char(id-1+'A')<<endl;
    }
    return 0;
}

B.The Child and Set (二进制的性质)

题意

让你在1-limit中选一个集合,使得集合元素的值等于sum

元素的值为编号的lowbit值

思路

lowbit值很好处理(废话)

然后lowbit的性质是绝对是2的次方，所以集合里面的元素值肯定都是相差多倍或者是相等的情况 所以我们就可以直接对1-limit中的lowbit值从大到小排序 每次取最大的小于等于sum的lowbit值,就行。

具体证明是 如果有一个值为x 那么如果你不去他，你就只能取x/2，和x/4 和x/8，会发现这些值就算都取你也得不到原来的x

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
struct node{
    int num;
    int lowbit;
}my[maxn];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int sum,limit;
    cin>>sum>>limit;
    for(int i=1;i<=limit;i++){
        my[i].num=i;
        my[i].lowbit=i&(-i);
    }
    sort(my+1,my+1+limit,[](node a,node b)
         {
            return a.lowbit>b.lowbit;
         });
    vector<int>ve;
    for(int i=1;i<=limit;i++){
        if(my[i].lowbit<=sum){
            ve.push_back(my[i].num);
            sum-=my[i].lowbit;
        }
    }
    if(sum)cout<<-1<<endl;
    else {
        cout<<ve.size()<<endl;
        for(int i=0;i<ve.size();i++)cout<<ve[i]<<" ";
    }
    return 0;
}

C.The Child and Toy (贪心)

题意

给出n个点m条边让你把所有点删除 删除的花费是所有和该点连接的点的值的总和。

问你吧所有点删除的最小值是多少

思路

首先把删点转换成删边,根据题意 在删点的过程中也相当于删边。

根据题意对于每条边删去的花费是其中一个点的费用，所以就每次贪心取每条边的费用最小的那个点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int a[maxn];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n,m,sum=0;
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>a[i];
    while(m--){
        int u,v;
        cin>>v>>u;
        sum+=min(a[v],a[u]);
    }
    cout<<sum;
    return 0;
}

D.The Child and Zoo (最大生成树)

题意

给出一个图，对于任意两个点之间的路径中的最小值的和，让你把这个值最大化 输出他的平均值。

思路

首先想到最大生成树，可以保证每两个点之间的路径都是最大费用，然后对于两个子树合并，他们的答案就是子树结点数的乘积（方案数）再乘上这条关键边的费用。

因为我们只求了单向的一次值，所以需要把值乘2 才算是答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
struct Edge{
    int u,v;
    ll value;
    bool operator <( const Edge &a)const {
        return value>a.value;
    }
};
vector<Edge>G;
ll a[maxn];
int fa[maxn];
int sz[maxn];
int Find(int u){
    return u==fa[u]?u:fa[u]=Find(fa[u]);
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>a[i];
    while(m--){
        int u,v;
        cin>>u>>v;
        G.push_back(Edge{u,v,min(a[v],a[u])});
    }
    for(int i=1;i<=n;i++)sz[i]=1,fa[i]=i;
    ll ans=0;
    sort(G.begin(),G.end());
    for(int i=0;i<G.size();i++){
        int aa=Find(G[i].u),bb=Find(G[i].v);
        if(aa^bb){
            ans+=1LL*(2LL*sz[aa]*sz[bb])*1LL*G[i].value;
            fa[aa]=bb;
            sz[bb]+=sz[aa];
        }
    }
    cout<<fixed<<setprecision(6);
    cout<<1.0*ans/n/(n-1);
    return 0;
}

E.The Child and Polygon （基础几何+区间DP）

题意

给出一个简单多边形，其中的点根据顺时针或者逆时针排列

让你把这个多边形分成许多三角形满足以下情况

1.三角形的每个端点都在简单多边形的端点上

2.简单多边形的每一条边都要属于一个三角形

3.三角形之间不能重叠和有间隙

4.每个三角形都必须严格在多边形中

5.三角形的每一条边都要连接多边形的两个端点

思路

一开始毫无思路….

首先 利用分治的想法把一整个多边形变成两个小多边形 那么大多边形的答案就是小多边形各自的答案相乘（比如小A的答案是4种，小B的答案是5种，那么他们各自的组合就是4*5=20种），然后把就是怎么分多边形了，假设我们现在的多边形是(0-(n-1))这几个大点构成的，那么小多边形之间的分割点 肯定就是在这些（0~n-1）点之间的某个点 也就是 1，2，3，->n-2 ，那么什么时候结束呢，如果两个点之间没有间隔了就结束。也就是i+1=j了的时候

这时候发现有些分割点并不能取，能取的分割点 和边界也必须要符合构成一个三角形

如下图

\E1.png)

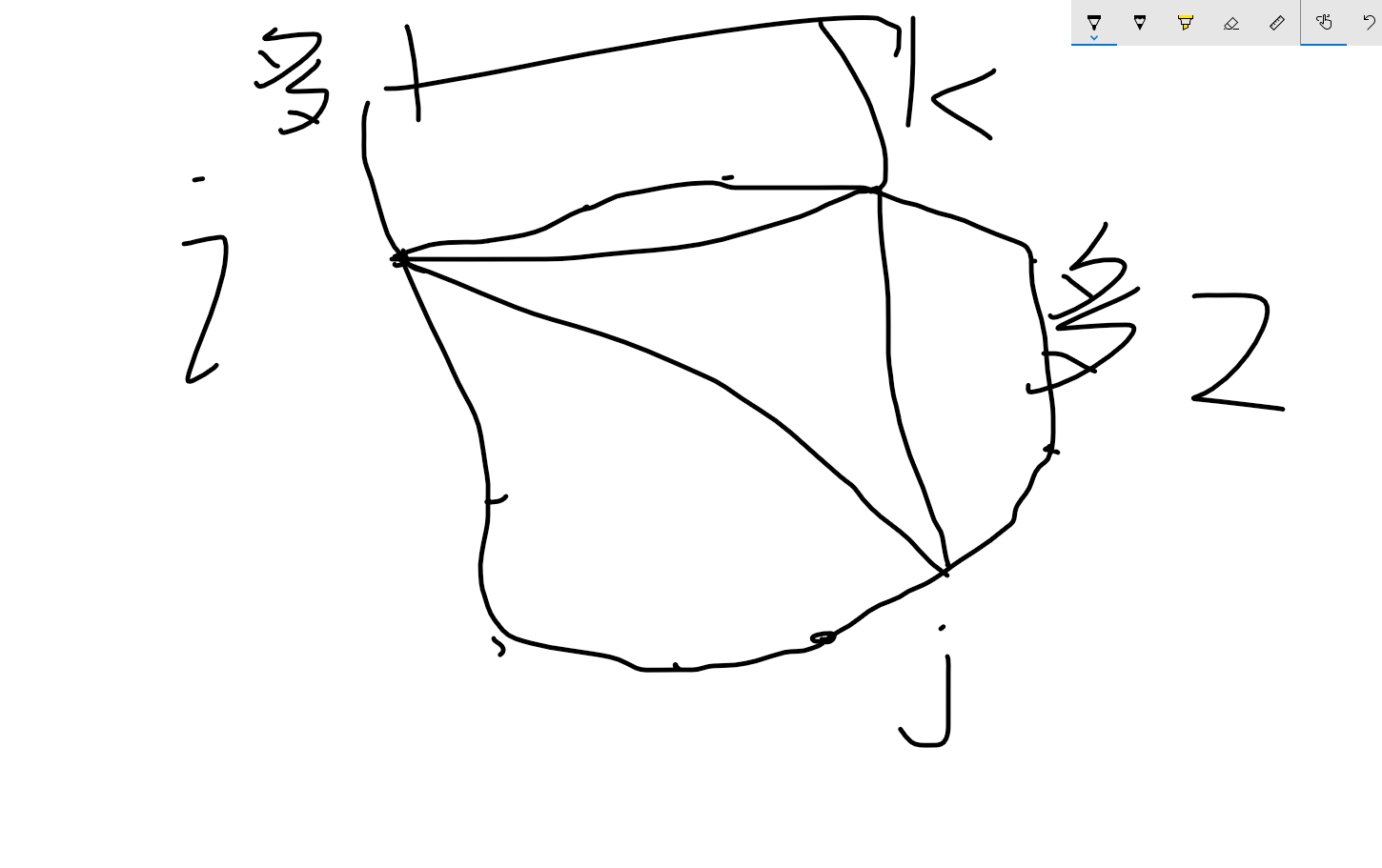
另一种情况不能选择这个K点为分割点

\E2.png)

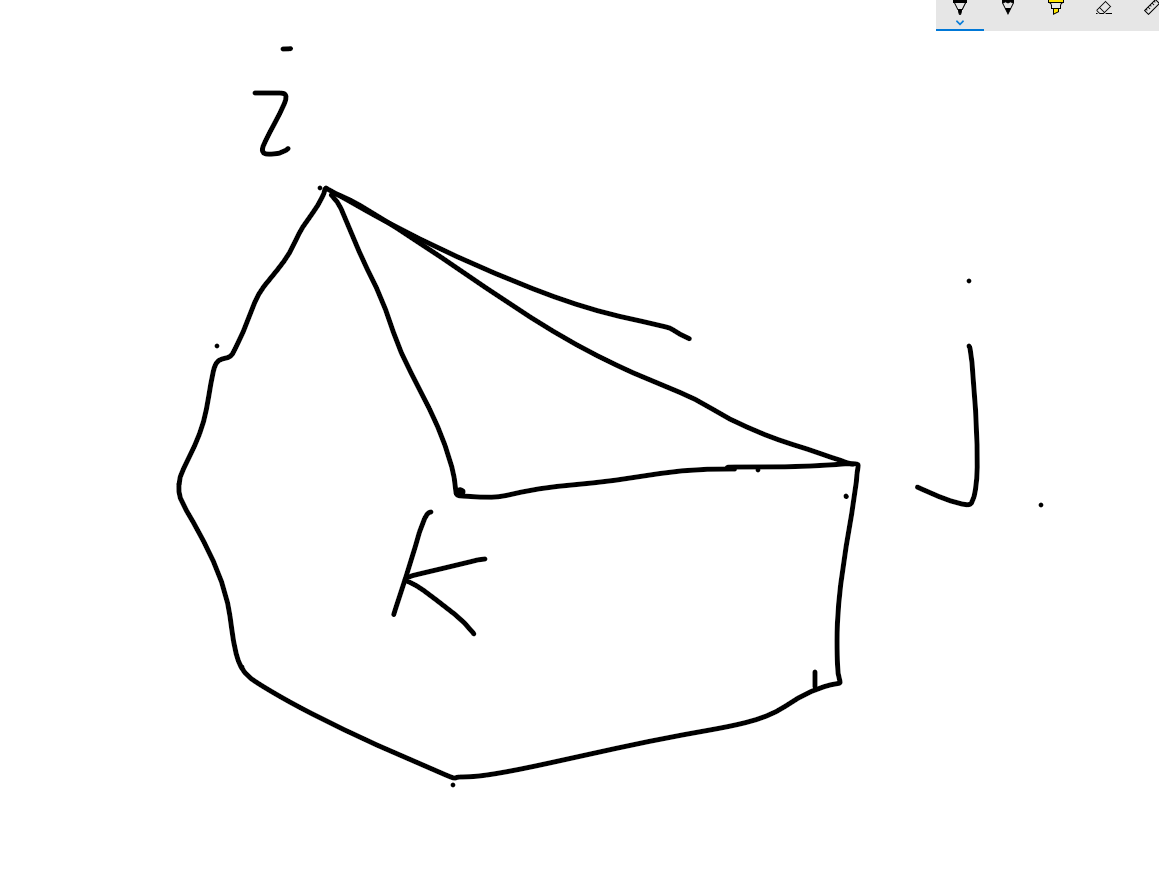
这种情况是K在i-j这条线之内的情况

然后那么怎么判断这个点在不在呢，就直接判断线段i -k 和线段k -j是不是在同一个方向的就行.

为了统一我们可以在输入数据的时候就统一指定为顺时针

ps：给出一个序列的点，判断它是顺时针还是逆时针：计算连续两个点的叉积，包括第一个和最后一个，求他们的和，大于0为顺时针，小于0为逆时针。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
struct node{
    ll x,y;
    node operator -(const node &a)const{
        return node{x-a.x,y-a.y};
    }
    ll operator *(const node &a)const{
        return x*a.y-y*a.x;
    }
}my[550];
ll dp[250][250];
ll dfs(int l,int r){
    if(l+1==r)return 1;
    if(~dp[l][r])return dp[l][r];
    ll ans=0;
    for(int i=l+1;i<r;i++){
        if((my[l]-my[i])*(my[i]-my[r])<=0)continue;
        ans+=dfs(l,i)*dfs(i,r)%mod;
        ans%=mod;
    }
    return dp[l][r]=ans;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n;
    cin>>n;
    for(int i=0;i<n;i++)cin>>my[i].x>>my[i].y;
    ll ans=0;
    for(int i=0;i<n;i++){
        ans+=my[i]*my[(i+1)%n];
    }
    if(ans<0){
        reverse(my,my+n);
    }
    memset(dp,-1,sizeof(dp));
    cout<<dfs(0,n-1)<<endl;
    return 0;
}

Diposting di | Edited on

传送门

A - Nearly Lucky Number （签到）

题意

给出一个数字 求其中7和4的数目是否是7和4组成

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+9;
const int maxn=3e5+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;

int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    string s;
    cin>>s;
    int len=s.size();
    int sum=0;
    for(int i=0;i<len;i++){
        if(s[i]=='4'||s[i]=='7'){
            sum++;
        }
    }
    if(sum==4||sum==7){
        cout<<"YES"<<endl;
    }
    else cout<<"NO"<<endl;
    return 0;
}

B - Lucky String(贪心构造)

题意

让你构造一个字典序最小字符串 其中每个字符之间的间隔都必须是4和7组成的幸运数字

思路

直接ABCD四个一循环就行

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+9;
const int maxn=3e5+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
char s[5]={'a','b','c','d'};
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n;
    cin>>n;
    for(int i=0;i<n;i++){
        cout<<s[i%4];
    }
    return 0;
}

C - Lucky Sum of Digits （构造）

题意

给出一个N问你能否存在一个由4和7组成并且各位之和为N的数字并且各位之和为N的数字

有输出最小的 没有输出-1

思路

7×A+4×B=N

要最小 那就是长度最短 所以经可能让7多

因为数据1e6 直接枚举时间过得去

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+9;
const int maxn=3e5+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
char s[5]={'a','b','c','d'};
int seven,four;
string ans="999";
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n;
    cin>>n;
    bool flag=0;
    for(int i=0;i<=n/7;i++){
        int fo=n-i*7;
        if(fo%4==0){
            seven=i;
            flag=1;
            four=fo/4;
        }
    }
    if(!flag)cout<<-1;
    else{
        for(int i=0;i<four;i++){
            cout<<4;
        }
        for(int i=0;i<seven;i++)
            cout<<7;
    }
    return 0;
}

D - Lucky Probability (区间枚举)

题意

出个两个（P,V）范围在1e9的正整数区间，分别从其中随机选出一个数，选出的两个数作为一个新区间的左右端点。要求新区间内的幸运数刚好为k个的概率（幸运数指一个数的数位只有4或7）。

思路

直接做肯定爆炸，我们发现1e9范围内最多2^10个幸运数字

然后我们就直接判断幸运数字 的区间，使得一个在min，一个在max

注意就是K==1的时候要去重一下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+9;
const int maxn=3e5+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
ll has[maxn];
int num=0;
ll get(ll al,ll ar,ll ql,ll qr){
    ll l=max(al,ql);
    ll r=min(ar,qr);
    return l<=r?(r-l+1LL):0;
}
vector<ll>pre,nex;

void init(){
    pre.push_back(0);
    for(int i=0;i<10;i++){
        nex.clear();
        for(auto i:pre){
            ll now=i*10LL+4LL;
            nex.push_back(now);
            has[++num]=now;
            now=i*10LL+7LL;
            nex.push_back(now);
            has[++num]=now;
        }
        pre=nex;
    }
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    init();
    ll pl,pr,vl,vr,k;
    cin>>pl>>pr>>vl>>vr>>k;
    ll down=1LL*(pr-pl+1LL)*(vr-vl+1LL);
    ll ans=0;
    for(ll i=1;i<=2040;i++){
        ll pre=i,next=i+k-1;
        ans+=get(has[pre-1]+1,has[pre],pl,pr)*get(has[next],has[next+1]-1,vl,vr);
        ans+=get(has[pre-1]+1,has[pre],vl,vr)*get(has[next],has[next+1]-1,pl,pr);
    }
    if(k==1){
        for(int i=1;i<=2040;i++){
            ans-=get(has[i],has[i],pl,pr)*get(has[i],has[i],vl,vr);
        }
    }
    cout<<fixed;
    cout<<setprecision(13)<<double(ans*1.0/down*1.0)<<endl;
    return 0;
}

E - Lucky Tree(并查集)

题意

给你一个树，让你求有多少个三元组(a,b,c)满足a,b,c不同并且a到b至少有一个为幸运数字的边 a到c之间也至少有一个幸运数字的边

问这个三元组有多少个

思路

首先 没有幸运数字为边的点可以缩成一个点，因为他们之间肯定不能连线对答案没有贡献

这时候其他的点就和这个点相连就有贡献了

所以直接并查集缩点就行

比赛题目没看完就结束了 难过

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+10;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int fa[maxn],sz[maxn];
int find(int x){
    return x==fa[x]?x:fa[x]=find(fa[x]);
}
void fix(int a,int b){
    a=find(a),b=find(b);
    if(sz[a]>sz[b])swap(a,b);
    sz[b]+=sz[a];
    sz[a]=0;
    fa[a]=b;
}
bool luck(int x){
    while(x){
        if(x%10!=4&&x%10!=7)return false;
        x/=10;
    }
    return true;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)sz[fa[i]=i]=1;
    for(int i=1;i<n;i++){
        int a,b,c;
        cin>>a>>b>>c;
        if(!luck(c))fix(a,b);
    }
    ll ans=0;
    for(int i=1;i<=n;i++){
        if(sz[i]){
            ans+=1LL*(sz[i])*(1LL*n-sz[i])*(n-sz[i]-1LL);
        }
    }
    cout<<ans;
    return 0;
}

Diposting di | Edited on

传送门

A - Football （签到）

题意

问有没有连续的七个1或者七个0

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const ll mod=1e9+7;
const int maxn=5e5+50;
const int inf=1e8;
char s[150];
int zero[150],one[150];
int main()
{
    cin>>s+1;
    int len=strlen(s+1);
    for(int i=1;i<=len;i++){
        if(s[i]=='1'){
            one[i]=one[i-1]+1;
            zero[i]=0;
        }
        else
            zero[i]=zero[i-1]+1,one[i]=0;
        if(zero[i]>=7||one[i]>=7)puts("YES"),exit(0);
    }
    puts("NO");
    return 0;
}

B - Lucky Numbers (easy) (dfs)

题意

问你大于等于N的最小的只有4和7组成的最小的相同4/7个数的数是多少

思路

直接爆搜

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const ll mod=1e9+7;
const int maxn=5e5+50;
const ll inf=1e17;
ll ans=inf;
ll n;
void dfs(ll num,ll a,ll b){
    if(a==b&&num>=n)ans=min(ans,num);
    if(num>n*100)return;
    dfs(num*10+4,a+1,b);
    dfs(num*10+7,a,b+1);
}
int main()
{
    cin>>n;
    dfs(0,0,0);
    cout<<ans<<endl;
    return 0;
}

C - Hockey (模拟 ，题意杀)

题意

给你n个禁用子串w1,w2……wn，在主串w中找出与禁用相同的的子串用字母letter替换。若要替换的子串中有字母与letter相同，

那么就按字典序（PS：如果letter是a，那是b啦，不然就用a好了）去替换。输出时大小写保持不变。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const ll mod=1e9+7;
const int maxn=1e3+50;
const ll inf=1e17;
string s[maxn],sa[maxn],w,wa;
bool m[maxn];
char ned;
string to(string s){
    for(int i=0;s[i];i++)
        if(s[i]>='A'&&s[i]<='Z')s[i]=tolower(s[i]);
    return s;
}
int main()
{
    int n;
    cin>>n;
    for(int i=0;i<n;i++)cin>>s[i],sa[i]=to(s[i]);
    cin>>w;
    wa=to(w);
    cin>>ned;ned=tolower(ned);
    for(int i=0;i<wa.size();i++){
        for(int j=0;j<n;j++){
            if(wa.substr(i,sa[j].size())==sa[j]){
                for(int k=i;k<i+sa[j].size();k++)m[k]=1;
            }
        }
    }
    for(int i=0;i<wa.size();i++){
        if(m[i]){
            if(wa[i]==ned){
                char tm;
                if(wa[i]=='a')tm='b';
                else tm='a';
                if(w[i]>='A'&&w[i]<='Z')w[i]=tm-32;
                else w[i]=tm;
            }
            else if(w[i]>='A'&&w[i]<='Z')w[i]=ned-32;
            else w[i]=ned;
        }
    }
    cout<<w<<endl;
    return 0;
}

D - Volleyball (最短路)

题意

有n个地方，m条路，一个人要从x到y,他要打车走，每条路上都有出租车，出租车走的距离为t，收c元，求从x到y最小花费

思路

重建图算出每个点能去哪些点 然后跑bfs或者dij

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const ll mod=1e9+7;
const int maxn=1e3+50;
const ll inf=1e17;

int n,m;
struct node{
    int to;
    ll w;
    bool operator <(const node &a)const{
        return w>a.w;
    }
};
vector<node>G[maxn],G2[maxn];
int x,y;
ll t[maxn],c[maxn];
ll val[maxn];
priority_queue<node>Q;
void dij(int st){
    for(int i=1;i<=n;i++)val[i]=inf;
    val[st]=0;
    while(!Q.empty())Q.pop();
    Q.push(node{st,0});
    while(!Q.empty()){
        node now=Q.top();
        Q.pop();
        int u=now.to;
        ll w=now.w;
        if(val[u]>t[st])break;
        if(u!=st&&val[u]<=t[st])G2[st].push_back({u,0});
        for(int i=0;i<G[u].size();i++){
            int to=G[u][i].to;
            if(val[to]>val[u]+G[u][i].w){
                val[to]=val[u]+G[u][i].w;
                Q.push(node{to,val[to]});
            }
        }
    }
}
void dij2(){
    for(int i=1;i<=n;i++)val[i]=inf;
    val[x]=c[x];
    while(!Q.empty())Q.pop();
    Q.push(node{x,val[x]});
    while(!Q.empty()){
        node now=Q.top();Q.pop();
        int u=now.to;
        for(int i=0;i<G2[u].size();i++){
            int v=G2[u][i].to;
            ll tmp=0;
            if(v==y)tmp=c[v];
            if(val[v]>val[u]+c[v]-tmp){
                val[v]=val[u]+c[v]-tmp;
                Q.push(node{v,val[v]});
            }
        }
    }
}
int main()
{
    cin>>n>>m;
    cin>>x>>y;
    for(int i=1;i<=m;i++){
        int u,v,w;
        cin>>u>>v>>w;
        G[u].push_back({v,w});
        G[v].push_back({u,w});
    }
    for(int i=1;i<=n;i++){
        cin>>t[i]>>c[i];
        dij(i);
    }
    if(x==y)puts("0"),exit(0);
    dij2();
    if(val[y]==inf)val[y]=-1;
    cout<<val[y]<<endl;
    return 0;
}

E - Horse Races (数位DP)

题意

求区间内幸运数字（4/7）间隔不超过K的数字的个数 区间大小为$10^{1000}$

思路

一眼数位DP

$dp[pos][dis][yes]$ 表示位置在pos +上一个幸运数字和现在隔多少位置+是否已经有间隔不超过K的幸运数字

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const ll mod=1e9+7;
const int maxn=5e5+50;
const ll inf=1e16;
int k;
char st[2000],ed[2000];
ll dp[2000][3000][2];

int num[2000];

ll dfs(int pos,int ok,bool limit,int yes){
    if(pos==-1)return yes;
    if(!limit&&dp[pos][ok][yes]!=-1)return dp[pos][ok][yes];
    int up=limit?num[pos]:9;
    ll ans=0;
    for(int i=0;i<=up;i++){
        int dis=ok+1;
        if(i==4||i==7){
            if(ok<=k)dis=0;
            else dis=1;
        }
        ans+=dfs(pos-1,dis,limit&&i==up,dis==0||yes);
        ans%=mod;
    }
    if(!limit)dp[pos][ok][yes]=ans;
    return ans;
}

ll acc(char x[]){
    int len=strlen(x);
    for(int i=0;i<len;i++)num[i]=x[len-1-i]-'0';
    return dfs(len-1,k+5,true,false);
}
int main()
{
    int t;
    memset(dp,-1,sizeof(dp));
    ios::sync_with_stdio(false);
    cin>>t>>k;
    while(t--){
        cin>>st>>ed;
        int lena=strlen(st),p=lena-1;
        while(st[p]=='0')st[p--]='9';
        st[p]=st[p]-1;
        cout<<(acc(ed)-acc(st)+mod)%mod<<endl;
    }
    return 0;
}

Diposting di | Edited on

传送门

A. Hard to prepare

题意

一个环形的 n 的列表每个数都是 0 到 2^k-1，求相邻两个数同或不为 0 的方案数。同或 ->相同为1，不同为0

思路

利用环形涂色的公式，稍微改改

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=1e6+50;
//const ll inf=0x3f3f3f3f3f3f3f3fLL;
const int inf=500;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
#define pp pair<int,int>
int n,m,l,k;
char s[4];
int flag[11];
ll kk=1;
ll dp[maxn];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int t;
    cin>>t;
    while(t--){
        cin>>n>>k;
        kk=1;
        for(int i=1;i<=k;i++){
            kk=(kk*2)%mod;
        }
        ll l=(kk-1+mod)%mod;///在一个N-2个格子环中加入一个格子的种类数即An-2 * (M-1)
        ll r=(kk-2+mod)%mod;///
        dp[1]=kk;
        dp[2]=(dp[1]*l)%mod;
        for(int i=3;i<=n;i++){
            dp[i]=((dp[i-2]*l)%mod+((dp[i-1]-dp[1]+mod)%mod*(r)%mod)%mod)%mod;
        }
        cout<<dp[n]<<endl;
    }
    return 0;
}

B. BE, GE or NE

题意

两人博弈，每人轮流选择可以 +ai 或 −bi 或 ∗(−1)，两个人分别要最终大于或小于某个数，值不能超过100，和少于-100，奇数A选，偶数B选。求结果。

思路

记忆化搜索，状态是 (当前轮次, 当前分数)。注意数组的下标不能为负数 所以值都+200

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=1e6+50;
//const ll inf=0x3f3f3f3f3f3f3f3fLL;
const int inf=500;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
#define pp pair<int,int>
int n,m,l,k;
int dp[1010][600];
int a[1010],b[1010],c[1010];
int dfs(int i,int value){
  //  cout<<"i=="<<i<<endl;
    if(i>n)return value-200;///超界限
    if(dp[i][value]!=500)return dp[i][value];///走过了
   // cout<<"lai"<<endl;
    if(i&1){///男生
       // cout<<"我是男生"<<endl;
        int now=value-200;///变成正常的
        int ans=-200;///最低值
        if(a[i]>0){
           int k=min(100,now+a[i]);   ///保证不超出去
           int kk=dfs(i+1,k+200);  ///探寻下一个
            ans=max(ans,kk);
        }
        if(b[i]>0){
           int k=max(-100,now-b[i]);///最小的
           int kk=dfs(i+1,k+200);
            ans=max(ans,kk);
        }
        if(c[i]==1){ ///
            int kk=dfs(i+1,-now+200);
            ans=max(ans,kk);
        }
        dp[i][value]=ans;
    }
    else{//女生
        int now=value-200;
        int ans=200;
        if(a[i]>0){
           int k=min(100,now+a[i]);
           int kk=dfs(i+1,k+200);
            ans=min(ans,kk);
        }
        if(b[i]>0){
           int k=max(-100,now-b[i]);
           int kk=dfs(i+1,k+200);
            ans=min(ans,kk);
        }
        if(c[i]==1){
            int kk=dfs(i+1,-now+200);
            ans=min(ans,kk);
        }
        dp[i][value]=ans;
    }
    return dp[i][value];
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    cin>>n>>m>>k>>l;
    for(int i=1;i<=n;i++){
        cin>>a[i]>>b[i]>>c[i];
    }
    for(int i=0;i<=1005;i++)
    for(int j=0;j<=500;j++)dp[i][j]=500;
    int anw=dfs(1,m+200);
    if(anw>=k)cout<<"Good Ending"<<endl;
    else if(anw<=l)cout<<"Bad Ending"<<endl;
    else cout<<"Normal Ending"<<endl;
    return 0;
}

F. Features Track

题意

每帧出现一对数字，求一对数字连续出现的最长帧数。

思路

这题读半天都没懂题意，读懂之后直接map+pair

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
#define pp pair<int,int>
char s[1100000];
int a[1100000];
map<pp,int>flag;
map<pp,int>sum;
map<pp,int>now;
map<pp,int>anw;
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int t;
    cin>>t;
    while(t--){
        int n;
        cin>>n;
        int num=0;
        flag.clear();
        sum.clear();
        now.clear();
        anw.clear();
        for(int i=0;i<n;i++){
            int k;
            cin>>k;
            now.clear();
            for(int j=0;j<k;j++){
                int a,b;
                cin>>a>>b;
                if(now[make_pair(a,b)]==0){
                    now[make_pair(a,b)]=1;
                    sum[make_pair(a,b)]++;
                    if(sum[make_pair(a,b)]>anw[make_pair(a,b)]){
                        anw[make_pair(a,b)]=sum[make_pair(a,b)];
                        if(anw[make_pair(a,b)]>num){
                            num=anw[make_pair(a,b)];
                        }
                    }
                }
            }
            for(auto k:sum){
                if(now[k.first]==0){
                    sum[k.first]=0;
                }
            }

        }
        cout<<num<<endl;
    }
    return 0;
}

G. Trace

题意

堆叠若干个以原点为左下角的矩形，求看得到的右边界和上边界的总长度。注意新的会覆盖久的，所以从后往前最好了

思路

分别对x和y 从后往前搞,如果 后面有小于当前值的 就用当前值减去最大的小于它的值，如果没有就直接加上。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
#define pp pair<int,int>
map<ll,int>mp;
ll a[55000],b[55000];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n;
    cin>>n;
    map<ll,int>::iterator it;
    for(int i=0;i<n;i++){
        cin>>a[i]>>b[i];
    }
    mp.clear();
    ll sum=0;
    for(int i=n-1;i>=0;i--){
        it=mp.lower_bound(a[i]);
        if(mp.empty()||it==mp.begin()){//如果找不到;
            sum+=a[i];
        }
        else{
            it--;
            sum+=(a[i]-it->first);
        }
        mp[a[i]]++;
    }
    mp.clear();
    for(int i=n-1;i>=0;i--){
        it=mp.lower_bound(b[i]);
        if(mp.empty()||it==mp.begin()){//如果找不到;
            sum+=b[i];
        }
        else{
            it--;
            sum+=(b[i]-it->first);
        }
        mp[b[i]]++;
    }
    cout<<sum<<endl;
    return 0;
}

H. Ryuji doesn’t want to study

题意

求

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<string>
#include<cstring>
#include<vector>
#include<queue>
#include<map>
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
#define N 100005
typedef long long ll;
using namespace std;

ll tree[N<<3],lazy[N<<3],a[N],s[N];
ll n,m;
void pushup(ll rt){
    tree[rt]=tree[rt<<1]+tree[rt<<1|1];
}

void pushdown(ll len,ll rt){
    if(lazy[rt]){
        lazy[rt<<1]+=lazy[rt];
        lazy[rt<<1|1]+=lazy[rt];
        tree[rt<<1]+=lazy[rt]*(len-len/2);
        tree[rt<<1|1]+=lazy[rt]*(len/2);
        lazy[rt]=0;
    }
}

void build(ll l,ll r,ll rt){
    lazy[rt]=0;
    if(l==r){
        tree[rt]=s[l];
        return;
    }
    ll mid=(l+r)/2;
    build(lson);
    build(rson);
    pushup(rt);
}

void add(ll L,ll R,ll k,ll l,ll r,ll rt){
    if(L<=l&&R>=r){
        tree[rt]+=(r-l+1)*k;
        lazy[rt]+=k;
        return;
    }
    pushdown(r-l+1,rt);
    ll mid=(l+r)/2;
    if(L<=mid) add(L,R,k,lson);
    if(R>mid) add(L,R,k,rson);
    pushup(rt);
}

long long query(ll L,ll R,ll l,ll r,ll rt){
    if(L<=l&&R>=r){
        return tree[rt];
    }
    pushdown(r-l+1,rt);
    ll mid=(l+r)/2;
    long long ans=0;
    if(L<=mid) ans+=query(L,R,lson);
    if(R>mid) ans+=query(L,R,rson);
    pushup(rt);
    return ans;
}

int main(){
    scanf("%lld %lld",&n,&m);
    a[0]=0;
    for(ll i=1;i<=n;i++){
        scanf("%lld",&a[i]);
    }
    for(ll i=1;i<=n;i++){
        s[i]=s[i-1]+a[i];
    }
    build(1,n,1);
    ll pos,x,y;
    ll ans,ans1,ans2;
    for(ll i=1;i<=m;i++){
        scanf("%lld %lld %lld",&pos,&x,&y);
        if(pos==1){
            ans1=query(x,y,1,n,1);
            if(x-1<1){
                ans2=0;
            }
            else {
                ans2=query(x-1,x-1,1,n,1);
            }
            ans2=ans2*(y-x+1);
            ans=ans1-ans2;
            printf("%lld\n",ans);
        }
        else{
            add(x,n,y-a[x],1,n,1);
            a[x]=y;
        }
    }

    return 0;
}
/*
6 100
1 2 5 7 3 4
1 3 5
2 4 6
1 3 5
2 3 7
1 1 6
2 3 6
1 1 4

*/

I. Characters with Hash

题意

温暖签到题,可是因为00这个数据变得不温暖QAQ

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
char s[1100000];
int a[1100000];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int t;
    cin>>t;
    while(t--){
        int n;
        char z;
        cin>>n>>z;
        cin>>s;
        int len=strlen(s);
        int num=0;
        int flag=0;
        for(int i=0;i<len;i++){
            a[i]=abs(z-s[i]);
            if(a[i]==0&&flag==0)continue;
            else if(a[i]>0&&a[i]<=9&&flag==0){
                num=1;
                flag=1;
                continue;
            }
            else{
                flag=1;
                num+=2;
            }
        }
        if(num==0)cout<<1<<endl;
        else
            cout<<num<<endl;
    }
    return 0;
}

J. Maze Designer

题意

一个N*M的矩形,每个格点到其邻近点的边有其权值,需要构建出一个迷宫,使得构建迷宫的边权之和最小,之后Q次查询,每次给出两点坐标,给出两点之间的最短路径

思路

队友结束后十分钟A的,打完之后我看了下大概是这样

可以把每个格点视作视作图的点,隔开两点的边视作图的边,则构建迷宫可以视作求其生成树,剩余的边就是组成迷宫的墙.因为要花费最小,所以使删去的墙权置最大即可,呢么就是求最大生成树即可.
然后每次查询相当于查这个最大生成树上任意两点的最短距离,到这一步就是个LCA板子题了.
所以:最大生成树+LCA

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<string>
#include<cstring>
#include<vector>
#include<queue>
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
#define N 250500
#define MOD 1e9+7
#define INF 0x3f3f3f3f
typedef long long ll;
using namespace std;

int fa[N];
struct sair{
    int x,y,v;
}A[750500];
struct ssair{
    int to,v;
};
vector<ssair>ve[N];
int depth[N];
int parent[N][25];
int gw[N][25];
int visit[N];
int n,m;
int MAX;

void dfs(int root,int pre,int d,int co){
	depth[root]=co;
	gw[root][0]=d;
	parent[root][0]=pre;
	visit[root]=1;
	for(int i=0;i<ve[root].size();i++){
		if(ve[root][i].to!=pre){
			dfs(ve[root][i].to,root,ve[root][i].v,co+1);
		}
	}
}

int lca(int u,int v){
	if(depth[u]<depth[v]){
		int t;
		t=u;
		u=v;
		v=t;
	}
	int ans=0;
	for(int k=0;k<=MAX;k++){
		if(((depth[u]-depth[v]) >> k) & 1){
			ans+=gw[u][k];
			u=parent[u][k];
		}
	}
	if(u==v){
		return ans;
	}
	for(int k=MAX;k>=0;k--){
		if(parent[u][k]!=parent[v][k]){
			ans+=gw[u][k];
			ans+=gw[v][k];
			u=parent[u][k];
			v=parent[v][k];
		}
	}
	ans+=gw[u][0];
	ans+=gw[v][0];
	return ans;
}

bool cmp(sair a,sair b){
    return a.v>b.v;
}

int Find(int x){
    int r=x;
    while(x!=fa[x]){
        x=fa[x];
    }
    int y;
    while(r!=x){
        y=fa[r];
        fa[r]=x;
        r=y;
    }
    return x;
}

int join(int x,int y){
    int xx=Find(x);
    int yy=Find(y);
    if(xx!=yy){
        fa[xx]=yy;
        return 1;
    }
    return 0;
}

int main(){
    std::ios::sync_with_stdio(false);
    int a,b;
    int q;
    char ch1,ch2;
    int m1,m2;
    cin>>n>>m;
    int sum=1;
    for(int i=1;i<=n*m+1;i++){
        fa[i]=i;
    }
    int co=0;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cin>>ch1>>m1>>ch2>>m2;
            if(ch1=='D'){
                A[co].x=(i-1)*n+j,A[co].y=A[co].x+n,A[co].v=m1;
                co++;
            }
            if(ch2=='R'){
                A[co].x=(i-1)*n+j,A[co].y=A[co].x+1,A[co].v=m2;
                co++;
            }
        }
    }
    sort(A,A+co,cmp);
    ssair S,E;
    for(int i=0;i<co;i++){
        if(join(A[i].x,A[i].y)){
            sum++;
            S.to=A[i].y,S.v=1;
            E.to=A[i].x,E.v=1;
            ve[A[i].x].push_back(S);
            ve[A[i].y].push_back(E);
            if(sum==n*m){
                break;
            }
        }
    }
    dfs(1,0,0,0);
    MAX=int((log(n*m*1.0)/log(2*1.0)));
    for(int i=1;i<=MAX;i++){
        for(int j=1;j<=n*m;j++){
            if(parent[j][i-1]==0){
                parent[j][i]=0;
            }
            else{
                parent[j][i]=parent[parent[j][i-1]][i-1];
                gw[j][i]=gw[j][i-1]+gw[parent[j][i-1]][i-1];
        		//cout<<gw[gw[j][i-1]][i-1]<<"  "<<gw[j][i]<<"  hhh"<<endl;
            }

        }
    }
    cin>>q;
    int x1,y1,x2,y2;
    int xx,yy;
    while(q--){
        cin>>x1>>y1>>x2>>y2;
        xx=(x1-1)*n+y1;
        yy=(x2-1)*n+y2;
        printf("%d\n",lca(xx,yy));
    }
}

Diposting di | Edited on

传送门

B.Call of Accepted

题意

类似于计算器,不过就是特殊了一个计算d,变成一个骰子的类似,2d3表示投了两次三面骰子,给你一串字符串，问你结果的最大最小值

思路

直接转化成后缀表达式,但是比赛的时候太单纯没有想到一些特殊情况所以GG

正确解法应该是把所有的情况都考虑,每一次计算都算出一个最大最小值,然后在新的计算的时候再通过最大最小值计算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
#include<bits/stdc++.h>
using namespace std;
map<char,int>L;
map<char,int>R;
typedef long long ll;
#define pp pair<int,int>
string ac(string str){
    string ret;
    stack<char>s;
    s.push('#');
    int len=str.length();
    for(int i=0;i<len;i++){
        char t=str[i];
        if(t=='(')s.push(t);
        else if(t==')'){
            while(s.top()!='('){
                ret+=s.top();
                s.pop();
                ret+=' ';
            }
            s.pop();
        }
        else if(t=='+'||t=='-'||t=='*'||t=='d'){
            while(L[s.top()]>=R[t]){
                ret+=s.top();
                ret+=' ';
                s.pop();
            }
            s.push(t);
        }
        else{
            while(isdigit(str[i]))
                ret+=str[i++];
            i--,ret+=' ';
        }
    }
    while(s.top()!='#'){
        ret+=s.top();
        ret+=' ';
        s.pop();
    }
    return ret;
}
pp operator+(pp a,pp b){
    int vec[]={a.first+b.first,a.first+b.second,a.second+b.first,a.second+b.second};
    sort(vec,vec+4);
    return{vec[0],vec[3]};
}
pp operator-(pp a,pp b){
    int vec[]={a.first-b.first,a.first-b.second,a.second-b.first,a.second-b.second};
    sort(vec,vec+4);
    return{vec[0],vec[3]};
}
pp operator*(pp a,pp b){
    int vec[]={a.first*b.first,a.first*b.second,a.second*b.first,a.second*b.second};
    sort(vec,vec+4);
    return{vec[0],vec[3]};
}
pp operator^(pp a,pp b){
    int vec[]={a.first,a.second,a.first*b.first,a.first*b.second,a.second*b.first,a.second*b.second};
    sort(vec,vec+6);
    return{vec[0],vec[5]};
}
pp solve(string str){
    stack<pp>s;
    int i=0;
    pp tmp;
    while(i<str.length()){
        if(str[i]==' '){
            i++;continue;
        }
        if(str[i]=='+')tmp=s.top(),s.pop(),tmp=tmp+s.top(),s.pop(),i++;
        else if(str[i]=='-')tmp=s.top(),s.pop(),tmp=s.top()-tmp,s.pop(),i++;
        else if(str[i]=='*')tmp=s.top(),s.pop(),tmp=s.top()*tmp,s.pop(),i++;
        else if(str[i]=='d'){
            tmp=s.top(),s.pop(),
            tmp=s.top()^tmp,s.pop(),
            i++;
        }
        else{
            int x=0;
            while(isdigit(str[i]))
                x=x*10+str[i++]-'0';
            tmp={x,x};
        }
        s.push(tmp);
    }
    return s.top();
}
int main(){
    L['+']=1,L['-']=1,L['*']=2,L['d']=3;
    R['+']=1,R['-']=1,R['*']=2,R['d']=3;
    string s;
    while(cin>>s){
        string tmp=ac(s);
        pp res=solve(tmp);
        cout<<res.first<<" "<<res.second<<endl;
    }
}

D. Made In Heaven

题意

N个点，M条边，起始点为s，结束为n，求s到n的第k短的路的长度，判断长度是否大于T，如果大于，输出“Whitesnake!”，否则输出“yareyaredawa”

思路

队友A的,我并不会这种K最短路….

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <queue>
#define MAXN 1005
#define MAXM 500005
#define INF 1000000000
using namespace std;
struct node
{
    int v, w, next;
}edge[MAXM], revedge[MAXM];
struct A
{
    int f, g, v;
    bool operator <(const A a)const {
        if(a.f == f) return a.g < g;
        return a.f < f;
    }
};
int e, vis[MAXN], d[MAXN], q[MAXM * 5];
int head[MAXN], revhead[MAXN];
int n, m, s, t, k;
void init()
{
    e = 0;
    memset(head, -1, sizeof(head));
    memset(revhead, -1, sizeof(revhead));
}
void Insert(int x, int y, int w)
{
    edge[e].v = y;
    edge[e].w = w;
    edge[e].next = head[x];
    head[x] = e;
    revedge[e].v = x;
    revedge[e].w = w;
    revedge[e].next =revhead[y];
    revhead[y] = e++;
}
void spfa(int src)
{
    for(int i = 1; i <= n; i++) d[i] = INF;
    memset(vis, 0, sizeof(vis));
    vis[src] = 0;
    int h = 0, t = 1;
    q[0] = src;
    d[src] = 0;
    while(h < t)
    {
        int u = q[h++];
        vis[u] = 0;
        for(int i = revhead[u] ; i != -1; i = revedge[i].next)
        {
            int v = revedge[i].v;
            int w = revedge[i].w;
            if(d[v] > d[u] + w)
            {
                d[v] = d[u] + w;
                if(!vis[v])
                {
                    q[t++] = v;
                    vis[v] = 1;
                }
            }
        }
    }
}
int Astar(int src, int des)
{
    int cnt = 0;
    priority_queue<A>Q;
    if(src == des) k++;
    if(d[src] == INF) return -1;
    A t, tt;
    t.v = src, t.g = 0, t.f = t.g + d[src];
    Q.push(t);
    while(!Q.empty())
    {
        tt = Q.top();
        Q.pop();
        if(tt.v == des)
        {
            cnt++;
            if(cnt == k) return tt.g;
        }
        for(int i = head[tt.v]; i != -1; i = edge[i].next)
        {
            t.v = edge[i].v;
            t.g = tt.g + edge[i].w;
            t.f = t.g + d[t.v];
            Q.push(t);
        }
    }
    return -1;
}
int main()
{
    int x, y, w, len;
    while(scanf("%d%d", &n, &m) != EOF)
    {
        init();
        scanf("%d%d%d%d", &s, &t, &k,&len);
        for(int i = 1; i <= m; i++)
        {
            scanf("%d%d%d", &x, &y, &w);
            Insert(x, y, w);
        }

        spfa(t);
        int ans=Astar(s, t);
        if(ans<=len&&ans!=-1){
            puts("yareyaredawa");
        }
        else{
            puts("Whitesnake!");
        }
    }
    return 0;
}

F. Fantastic Graph

题意

一个二分图，M条边，选用M条边的一些，令最后所有点的度数都在[l,r]内 ，可以Yes 否则 No

思路

网络流 solve by fsh

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
#include<iostream>
#include<cstring>
#include<queue>
#include<cstdio>
#include<string>
#include<algorithm>
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
#define mem(a,b) memset(a,b,sizeof(a))
const int N=20005;
const int M=200005;
const int INF=0x3f3f3f3f;
using namespace std;

int top;
int h[N],pre[N],g[N],cost[N];

struct Vertex{
    int first;
}V[N];

struct Edge{
    int v,next;
    int cap,flow;
}E[M];

void init(){
    for(int i=0;i<N;i++){
        V[i].first=-1;
    }
    top=0;
}

void add_edge(int u,int v,int c){
    E[top].v=v;
    E[top].cap=c;
    E[top].flow=0;
    E[top].next=V[u].first;
    V[u].first=top++;
}

void add(int u,int v,int c){
    add_edge(u,v,c);
    add_edge(v,u,0);
}

void set_h(int t){
    queue<int>Q;
    mem(h,-1);
    mem(g,0);
    h[t]=0;
    Q.push(t);
    while(!Q.empty()){
        int v=Q.front();
        Q.pop();
        ++g[h[v]];
        for(int i=V[v].first;~i;i=E[i].next){
            int u=E[i].v;
            if(h[u]==-1){
                h[u]=h[v]+1;
                Q.push(u);
            }
        }
    }
}

int Isap(int s,int t,int n){
    set_h(t);
    int ans=0,u=s;
    int d;
    while(h[s]<n){
        int i=V[u].first;
        if(u==s){
            d=INF;
        }
        for(;~i;i=E[i].next){
            int v=E[i].v;
            if(E[i].cap>E[i].flow&&h[u]==h[v]+1){
                u=v;
                pre[v]=i;
                d=min(d,E[i].cap-E[i].flow);
                //cost[i]=d;
                if(u==t){
                    while(u!=s){
                        int j=pre[u];
                        E[j].flow+=d;
                        E[j^1].flow-=d;
                        u=E[j^1].v;
                    }
                    ans+=d;
                    d=INF;
                }
                break;
            }
        }
        if(i==-1){
            if(--g[h[u]]==0) break;
            int hmin=n-1;
            for(int j=V[u].first;~j;j=E[j].next){
                if(E[j].cap>E[j].flow){
                    hmin=min(hmin,h[E[j].v]);
                }
            }
            h[u]=hmin+1;
            ++g[h[u]];
            if(u!=s){
                u=E[pre[u]^1].v;
            }
        }
    }
    return ans;
}

int main(){
    int n,m,s,t,k;
    int v,u,w;
    int L,R;
    int co=1;
    while(~scanf("%d %d %d",&n,&m,&k)){
        init();
        s=0,t=(n+m)*2+1;
        scanf("%d %d",&L,&R);
        for(int i=1;i<=m+n;i++){
            add(i*2-1,i*2,R);
        }
        for(int i=1;i<=n;i++){
            add(s,i*2-1,INF);
        }
        for(int i=n+1;i<=m+n;i++){
            add(i*2,t,INF);
        }
        for(int i=0;i<k;i++){
            scanf("%d %d",&u,&v);
           // add(u,v,1);
           add(u*2,(v+n)*2-1,1);
        }
        int now;
        int flag=0;
        int ans=Isap(s,t,n+m+2);
        for(int i=1;i<=(n+m)*2;i+=2){
            for(int j=V[i].first;~j;j=E[j].next){
                if(E[j].v==i+1){
                    if(E[j].flow<L){
                        flag=1;
                    }
                }
            }
        }
        if(flag){
            printf("Case %d: No\n",co++);
        }
        else{
            printf("Case %d: Yes\n",co++);
        }
        /*
        int refer=L*(n+m)/2;
        cout<<refer<<" "<<ans<<endl;
        if(ans<=refer){
            printf("Case %d: No\n",co++);
        }
        else{
            printf("Case %d: Yes\n",co++);
        }*/
    }
    return 0;
}

I. Lattice’s basics in digital electronics

题意

给一系列二进制到ASCII的映射，给出一个十六进制数，需要你转化为二进制01串，然后9位9位得取，前八位的1的个数如果是偶数，第九位为1，说明校验结果正确，或者1的个数为奇数，第九位为0，校验结果正确，校验结果正确则保留前八位，反之舍弃这九位，不足九位的直接舍弃。最后通过上面的映射，输出得到的ASCII码对应字符的前m个字符。（题意很迷，直接看hint比较好理解）

思路

直接模拟,注意大小写和个数限制

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
#include<algorithm>
#include <iostream>
#include <stdlib.h>
#include <string.h>
#include  <stdio.h>
#include   <math.h>
#include   <time.h>
#include   <vector>
#include   <bitset>
#include    <queue>
#include      <map>
#include      <set>
using namespace std;
typedef long long ll;
const ll mod=1000000007;
const int maxn=1e8+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int n,m;
struct node{
    string s;
    int num;
    int k;
}my[350];
int cmp(node a,node b){
    return a.s<b.s;
}
string str;
string now;
void init(){
    now="";
    int len=str.length();
    for(int i=0;i<len;i++){
        switch(str.at(i)){
        case '0':
            now+="0000";break;
        case '1':
            now+="0001";break;
        case '2':
            now+="0010";break;
        case '3':
            now+="0011";break;
        case '4':
            now+="0100";break;
        case '5':
            now+="0101";break;
        case '6':
            now+="0110";break;
        case '7':
            now+="0111";break;
        case '8':
            now+="1000";break;
        case '9':
            now+="1001";break;
        case 'A':
            now+="1010";break;
        case 'B':
            now+="1011";break;
        case 'C':
            now+="1100";break;
        case 'D':
            now+="1101";break;
        case 'E':
            now+="1110";break;
        case 'F':
            now+="1111";break;
        case 'a':
            now+="1010";break;
        case 'b':
            now+="1011";break;
        case 'c':
            now+="1100";break;
        case 'd':
            now+="1101";break;
        case 'e':
            now+="1110";break;
        case 'f':
            now+="1111";break;
        }
    }
}
int main()
{
    //std::ios::sync_with_stdio(false);
    //std::cin.tie(0);
    //std::cout.tie(0);
    int t;
    scanf("%d",&t);
    while(t--){
        scanf("%d%d",&m,&n);
        for(int i=0;i<n;i++){
            cin>>my[i].num;
            cin>>my[i].s;
            my[i].k=my[i].s.length();
        }
        sort(my,my+n,cmp);
        cin>>str;
        init();
       // cout<<now<<endl;
        int nowlen=now.length();
        string anw="";
        string haha="";
        for(int i=0;i<nowlen;i+=9){
            int endnum=0;
            if(i+8>=nowlen)break;
            for(int j=i;j<i+8;j++){
                if(now[j]=='1')endnum++;
            }
            if((endnum%2!=0)&&now[i+8]=='0'){
                anw+=now.substr(i,8);
               // cout<<endnum<<endl;
            //    cout<<"i=="<<i<<" "<<anw<<endl;
            }
            else if((endnum%2==0)&&now[i+8]=='1'){
                anw+=now.substr(i,8);
               // cout<<endnum<<endl;
            //    cout<<"i=="<<i<<" "<<anw<<endl;
            }
        }
      // cout<<"i m here"<<endl;
       // cout<<anw<<endl;
       int num=0;
        for(int i=0;i<anw.length();i++){
            haha+=anw[i];
            for(int j=0;j<n;j++){
                if(haha==my[j].s){
                    cout<<char(my[j].num);
                   // cout<<my[j].num<<"  "<<haha<<endl;
                    haha="";
                    num++;
                    break;
                }
            }
            if(num>=m)break;
        }
        cout<<endl;
    }
    return 0;
}

K. Supreme Number

题意

定义supreme number：一个数是素数，这个数的每一项都是1或素数，并且由这个数的每一位数组成的序列中，取出组成的任意子序列组成一个数，都是素数

求小于等于N的最大的supreme number

思路

直接打表发现最大到317

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include<algorithm>
#include <iostream>
#include <stdlib.h>
#include <string.h>
#include  <stdio.h>
#include   <math.h>
#include   <time.h>
#include   <vector>
#include   <bitset>
#include    <queue>
#include      <map>
#include      <set>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;

int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
char s[1200];
int prime[21]={1,2,3,5,7,11,13,17,23,31,37,53,71,73,113,131,137,173,311,317,10000};
void init(){
    int one=1;
    for(int i=1;i<=10000;i++){
        int flag=0;
        for(int j=2;j<=sqrt(i);j++){
            if(i%j==0){ flag=1;
                break;

            }
        }
    if(flag==0)cout<<one++<<"   "<<i<<endl;
    }
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int t;
    scanf("%d",&t);
    int tt=1;
    while(t--){
        scanf("%s",s);
        int len=strlen(s);
        printf("Case #%d: ",tt++);
        if(len>=4)printf("317\n");
        else{
            int num=0;
            for(int i=0;i<len;i++){
                num=num*10+s[i]-'0';
            }
            for(int i=0;i<21;i++){
                if(prime[i]>num){
                    printf("%d\n",prime[i-1]);
                    break;
                }
            }
        }
    }
    return 0;
}

Diposting di | Edited on

传送门

A. An Olympian Math Problem

题意

求

S%n;

思路

A

所以直接输出N-1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
ll n;
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int t;
    cin>>t;
    while(t--){
        cin>>n;
        cout<<n-1<<endl;
    }
    return 0;
}

B. The writing on the wall

题意

一个n*m的方格矩阵,有的格子被涂成了黑色,问该矩阵中有多少个子矩阵,子矩阵不包含黑色格子;

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#include<iostream>
#include<cstring>
#include<cstdio>
#include<string>
#include<cmath>
using namespace std ;

#define clr( a , x ) memset ( a , x , sizeof a )


int U[100005] , S[100005] , cur , c[100005][105] , d[100005][105], n , m ,k,a,b,xxx;

void solve () {
    clr ( U , 0 ) ;
    clr(c,0);
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            d[i][j]=1;
        }
    }
    cur=0;
    for(int i=0;i<k;i++){
        scanf("%d %d",&a,&b);
        d[a][b]=0;
    }
    for ( int i = 1 ; i <= n ; ++ i ) {
        for ( int j = 1 ; j <= m ; ++ j ) U[j] = d[i][j] == 1 ? U[j] + 1 : 0 ;
        cur = 0 ;
        S[++ cur] = 0 ;
        for ( int j = 1 ; j <= m + 1 ; ++ j ) {
            while ( U[j] < U[S[cur]] ) {
                c[max ( U[S[cur - 1]] , U[j] ) + 1][j - S[cur - 1] - 1] ++ ;
                c[U[S[cur]] + 1][j - S[cur - 1] - 1] -- ;
                -- cur ;
            }
            while ( cur >= 1 && U[j] == U[S[cur]] ) -- cur ;
            S[++ cur] = j ;
        }
    }
    for ( int i = 1 ; i <= n ; ++ i ) {
        for ( int j = 1 ; j <= m ; ++ j ) c[i][j] += c[i - 1][j] ;
    }
    for ( int i = 1 ; i <= n ; ++ i ) {
        for ( int j = m - 1 ; j >= 1 ; -- j ) c[i][j] += c[i][j + 1] ;
        for ( int j = m - 1 ; j >= 1 ; -- j ) c[i][j] += c[i][j + 1] ;
    }
    long long ans=0;
    for ( int i = 1 ; i <= n ; ++ i ) {
        for ( int j = 1 ; j <= m ; ++ j ) {
            ans+=c[i][j];
          //  printf ( "%d%c" , c[i][j] , j < m ? ' ' : '\n' ) ;
        }
    }
    printf("Case #%d: %lld\n",xxx++,ans);
}

int main () {

    int t;
    scanf("%d",&t);
    xxx=1;
    while(t--){
        scanf("%d %d %d",&n,&m,&k);
        solve () ;
    }

    return 0 ;
}

E. AC Challenge

题意

N道题目，每个题目有得分A和得分B还有K个前置题目,在答这题时必须要把前置题目都答了才行,每个题目答对的得分是A*答这题当前时间+得分B;

每道题会有前置的做题需求，给我们题目的价值表示方法，要我们求出做这些题目可以获得的做大价值。

思路

一开始以为是拓扑排序，后来看到只有二十道题目直接状态压缩枚举每道题是否答过。然后判断这个状态可否再答题每次比较最大值得出答案。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1000000007;
const int maxn=(1<<21)+50;
const int MAXN=2e7+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
ll a[50];
ll b[50];
ll now[maxn];//状态
ll dp[maxn];//状态的得分
ll num[maxn];//里面有多少个1
ll ok[maxn];//记录这个需要的条件
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n;
    cin>>n;
    for(int i=0;i<n;i++){
        cin>>a[i]>>b[i];
        int k;
        cin>>k;
        for(int j=0;j<k;j++){
            int p;
            cin>>p;p--;
            ok[i]|=(1<<p);
        }
    }
    ll sum=0;
    memset(dp,-inf,sizeof(dp));
    dp[0]=0;
    for(ll i=0;i<(1<<n);i++){
        ll k=i;
        for(int j=0;j<=21;j++){
            if(i&(1<<j))num[i]++;
        }
        if(dp[i]==-inf)continue;//如果当前状态不可能;
        sum=max(sum,dp[i]);
        for(int j=0;j<n;j++){
            if((i&(1<<j)))continue;
            if((i&(ok[j]))!=ok[j])continue;
            dp[i|(1<<j)]=max(dp[i|(1<<j)],dp[i]+(num[i]+1)*a[j]+b[j]);
        }

    }
    cout<<sum<<endl;
    return 0;
}

G. Lpl and Energy-saving Lamps

题意

给N个房间换灯泡，城堡N个房间，每个月获得M个灯泡，然后每个房间按顺序走过去，如果手上灯泡数量大于等这个房间的灯泡数量,就把这个房间的灯泡数量替换,下一个从第一个房间开始;然后询问第Q个月换了几个房间还剩几个灯泡；

思路

线段树维护区间最小值，如果左子树的最小值比当前值大就不管右子树，然后询问到叶子节点，替换完后把最小值置为inf更新有关联的结点，然后从当前位置到N再询问一次,知道询问不出来或者已经到达N

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1000000007;
const int maxn=1e5+50;
const int MAXN=2e7+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
const int inff=0x3f3f3f3f;
struct node{
    int id,l,r,val;
    int mi;
}my[maxn<<2];
int a[maxn];
int b[maxn];
void up(int i){
    if(my[i].l==my[i].r)return;
    if(a[my[i<<1].mi]<a[my[(i<<1)|1].mi])my[i].mi=my[i<<1].mi;
    else my[i].mi=my[(i<<1)|1].mi;
}
void build(int i,int l,int r){
    my[i].l=l;
    my[i].r=r;
    if(l==r){
        my[i].mi=my[i].val=l;
        b[l]=i;
        return;
    }
    int mid=(l+r)/2;
    build(i<<1,l,mid);
    build((i<<1)|1,mid+1,r);
    up(i);
}
int query(int i,int l,int r,int v){
    //cout<<"i=="<<i<<" "<<my[i].mi<<endl;
    if(a[my[i].mi]>v)return -1;
    if(my[i].l==my[i].r){
        if(a[my[i].mi]<=v)
        return my[i].mi;
        else return -1;
    }
    int mid=(my[i].l+my[i].r)/2;
    int ll=-1,rr=-1;
    if(l<=mid){
        ll=query(i<<1,l,mid,v);
    }
    if(ll!=-1)return ll;
    if(r>mid){
        rr=query((i<<1)|1,mid+1,r,v);
    }
    if(rr!=-1)return rr;
    return -1;
}
void update(int i){
    if(i==-1)return;
    a[i]=inff;
    int t=b[i];
    while(t){
        up(t);
        t/=2;
        up(t);
    }
}
int anw1[maxn],anw2[maxn];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n,m;
    while(cin>>n>>m){
        for(int i=1;i<=n;i++){
            cin>>a[i];
        }
        build(1,1,n);
        int one;
        one=0;
        int v=0;
        for(int j=1;j<=100000;j++){
            v+=m;
            int now=1;
            while(true){
                int mi=query(1,now,n,v);
               // cout<<"j=="<<j<<"mi=="<<mi<<endl;
                if(mi==-1)break;
               // cout<<"j=="<<j<<endl;
               // cout<<"mi=="<<mi<<endl;
               // cout<<"v=="<<v<<endl;
                v-=a[mi];
                one++;
                update(mi);
                now=mi+1;
            }
            anw1[j]=one;
            anw2[j]=v;
        }
        int q;
        cin>>q;
        while(q--){
            int d;
            cin>>d;
            cout<<anw1[d]<<" "<<anw2[d]<<endl;
        }
    }
    return 0;
}

I. Skr

题意

给你一个数字字符串问你数字字符串里面本质不同的回文字符串的数字和是多少；

思路

比赛的时候不会回文树所以放弃了，后面知道有的大佬用了马拉车+hash过了这题，有点后悔。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<string>
#include<map>
using namespace std;
#define ULL unsigned long long
#define ll long long
const int maxn=4000000+40;
const int mod=1e9+7;
ULL P = 1313131;
ULL sqr[maxn/2],has[maxn/2],V[maxn];
ll ha[maxn/2],tmp[maxn/2];
int Laxt[maxn],Next[maxn],cnt=0;
 
const int MOD = 2000007;

bool _insert(ULL Now)
{
       int u=Now%MOD;
       for(int i=Laxt[u];i;i=Next[i]){
        if(V[i]==Now) return true;
       }
       Next[++cnt]=Laxt[u];
       Laxt[u]=cnt;
       V[cnt]=Now;
       return false;
}
ll ans=0;
void _hash(int x,int y){
    ULL Now=has[y]-has[x-1]*sqr[y-x+1];
    if(!_insert(Now))
    {
		ans+=((ha[y]-ha[x-1]*tmp[y-x+1]%mod)%mod+mod)%mod;
		ans%=mod;
	}
} 
int r[maxn];
char c[maxn];
void _malacher()
{
    int R=0,Mid=0,Len;
    
    scanf("%s",c+1);
    Len=strlen(c+1);
    sqr[0]=tmp[0]=1;
    has[0]=ha[0]=0;
    for(int i=1;i<=Len;i++){
        sqr[i]=sqr[i-1]*P;
        has[i]=has[i-1]*P+c[i];
        tmp[i]=tmp[i-1]*10%mod;
        ha[i]=(ha[i-1]*10+c[i]-'0')%mod;
    }  
    
     for(int i=1;i<=Len;++i) {      
        _hash(i,i);
        if(R>i) r[i]=min(r[2*Mid-i],R-i);
        while(i+r[i]+1<=Len&&c[i+r[i]+1]==c[i-r[i]-1]){
            _hash(i-r[i]-1,i+r[i]+1);
            r[i]++;
        }
        if(i+r[i]>R) {
            R=i+r[i];
            Mid=i;
        }
    }
    
    cnt=0;Mid=0;R=0;
    memset(Laxt,0,sizeof(Laxt));
    memset(r,0,sizeof(r));
    for(int i=2;i<=Len;++i) {
        if(R>i) r[i]=min(r[2*Mid-i],R-i+1);
        while(i+r[i]<=Len&&c[i+r[i]]==c[i-r[i]-1]) {
            _hash(i-r[i]-1,i+r[i]);
            ++r[i];
        }
        if(i+r[i]-1>R) {
            R=i+r[i]-1;
            Mid=i;
        }
    }
    printf("%lld\n",ans);
}
int main()
{
    _malacher();
    return 0;
}

J. Sum

题意

一个数可以拆成两个因子,比如

但是也有的会拆成因子中有平方数的比如；12=2²×3，这样就不是题目需要的答案，

对于6我们可以拆成4个满足题目需求的分解例如 6=1×6=6×1=2×3=3×2总共有四种所以定义F(6)=4

现在要求求

思路

1.首先我们肯定知道素数只有1和自己两个因子所以素数就只有2,F(素数)=2；

2.如果不是素数那就肯定是由两个素数组成而来的,比如12(12=2²×3)是由2和3这两个素数得来的，但是如果12=4×3中间的4就是一个平方数所以不符合条件，但是4可以拿出一个2给3变成12=2×6这样就符合题目的条件

2.如果里面有一个素数的次方超过2比如

这里的2就算拿出一个给3也会变成4×6;这样4也是一个平方数;如果是2×12,这里这里的12里面包含一个平方数4也不行,所以超过3的数F(x)=0；

所以我们可以把一个数拆成无数个不同素数的各种方的乘积。

如果存在一个方超过2答案F(x)=0；

如果等于2说明他必须拆开,分布在两个因子中,所以贡献是1 就等于这是铁定的不能变的，

如果等于1说明他可以选和不选,所以贡献为2

所以就判断一个数的它因子的一次方是多少然后就这个数量的2次幂

最多的可能肯定是这个数的最小素数因子，然后判断答案是否有这个因子的二次方以上，如果是就为0，如果是2就忽略看其他的因子，如果是1就贡献2再看其他的因子；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1000000007;
const int maxn=2e7+50;
const int MAXN=2e7+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
ll n;
ll a[maxn];
int prime[maxn];
int minprime[maxn];
int sum[maxn];
void get(){
    for(int i=0;i<MAXN;i++)prime[i]=0;
    for(int i=2;i<=MAXN;i++){
        if(!prime[i]){
            prime[++prime[0]]=i;
            minprime[i]=i;
        }
        for(int j=1;j<=prime[0]&&prime[j]<=MAXN/i;j++){
            prime[prime[j]*i]=1;
            minprime[prime[j]*i]=prime[j];
            if(i%prime[j]==0)break;
        }
    }
}

int main()
{
   // std::ios::sync_with_stdio(false);
    //std::cin.tie(0);
    //std::cout.tie(0);
    int t;
    get();
    a[1]=1;
    for(int i=2;i<=MAXN;i++){
        int M=minprime[i];
        if(ll(M*M)<MAXN&&ll(M*M*M)<MAXN&&i%(M*M*M)==0)
            a[i]=0;
        else if((ll)M*M<maxn&&i%(M*M)==0)
            a[i]=a[((i/M)/M)];
        else a[i]=2*a[i/M];
    }
    for(int i=1;i<MAXN;i++){
        sum[i]=sum[i-1]+a[i];
    }
    scanf("%d",&t);
    while(t--){
        int n;
        scanf("%d",&n);
        printf("%d\n",sum[n]);
    }
    return 0;
}

L. Magical Girl Haze

题意

单源最短路，但是可以有最多K个免费的道路，然你求从1到N的最短距离;

思路

这题不是我写的,但是我赛后研究了一下解法,应该是把每个路都加上一层K的免费路线，这种解法叫做分层图,这类题都有一个特征就是把某些边变为0，或者是变为一个其他的数，我们只要把这个图拓展成K层。原来的一条边扩展成与下一层的一条边，这样再跑最短路算法就可以了。然后遍历每层你要到的那个终点选出最小的一个就可以了。

不过注意总的最大边数是 复杂度应该是O（K×E×logE)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
#include<bits/stdc++.h>
using namespace std;
int s,t,n,m,k;
long long d[100000+10][11];
const long long INF=0x3f3f3f3f3f3f3f3f;
typedef pair<int,int> pii;
vector<pii> G[100000+10];
bool visit[100000+10][11];
struct Node
{
    int id;
    int level;
    int dis;
    Node(int id,int level,int dis):id(id),level(level),dis(dis)
    {

    }
    bool operator <(const Node& X)const
    {
        return dis>X.dis;
    }
};

int main()
{

    int a,b,c,j;
    int T;
    scanf("%d",&T);
    while(T--){
        cin>>n>>m>>k;
        s=1,t=n;
        priority_queue<Node> pq;
        for(int i=0;i<=n+1;i++){
            for(int j=0;j<=10;j++){
                d[i][j]=INF;
            }
        }
        for(int i=0;i<n;i++)
            G[i].clear();
        for(int i=0;i<m;i++)
        {
            scanf("%d%d%d",&a,&b,&c);
            for(j=0;j<G[a].size();j++){
                if(G[a][j].first==b){
                    if(G[a][j].second>c){
                        G[a][j].second=c;
                    }
                    break;
                }
            }
            if(j==G[a].size())
                G[a].push_back(make_pair(b,c));
        }
        memset(visit,0,sizeof(visit));
        for(int i=0;i<n;i++)
            for(int j=0;j<=k;j++)
                d[i][j]=INF;
        d[s][0]=0;
        pq.push(Node(s,0,0));
        while(!pq.empty())
        {
            Node X=pq.top();
            pq.pop();
            int x=X.id;
            int lv=X.level;
            if(visit[x][lv]==true)
                continue;
            else
            {
                visit[x][lv]=true;
                vector<pii>::iterator it;
                for(it=G[x].begin();it!=G[x].end();it++)
                {
                    int y=(*it).first;
                    int u=(*it).second;
                    if(u+d[x][lv]<d[y][lv])//同一层
                    {

                        d[y][lv]=u+d[x][lv];
                        pq.push(Node(y,lv,d[y][lv]));
                    }
                    if(lv<k)
                        if(d[x][lv]<d[y][lv+1])//不同层
                        {
                            d[y][lv+1]=d[x][lv];
                            pq.push(Node(y,lv+1,d[y][lv+1]));
                        }
                }
            }
        }
        long long ans=d[t][0];
        for(int i=0;i<=k;i++)
        {
            ans=min(ans,d[t][i]);
        }
        cout<<ans<<endl;
    }
    return 0;
}

Diposting di | Edited on

传送门

A. Magic Mirror

题意

签到题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
string s;
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int t;
    cin>>t;
    while(t--){
        cin>>s;
        for(int i=0;i<s.length();i++){
            if(s[i]<='Z'&&s[i]>='A'){
                s[i]+=32;
            }
        }
        if(s=="jessie"||s=="jessie"){
            cout<<"Good guy!"<<endl;
        }
        else{
            cout<<"Dare you say that again?"<<endl;
        }
    }
    return 0;
}

B. Mathematical Curse

题意

有一个包含n个非零整数的序列和一个含有m个字符的字符串s，字符只可能是 ‘+’, ‘-‘, ‘*’, ‘/‘ 四种，有一个初始值 k

现要从序列中取出一个含有m个数的子序列{a1, a2, .. , am}，求 k 和 m 个数进行运算后的最大值

要按照原序列的顺序进行运算

如：

4 4 5

1 2 3 4

+-*/

ans = ((((5 + 1) - 2) * 3) / 4)

思路

solve by lx

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
#include <bits/stdc++.h>

using namespace std;

const int mod=1000000007;
#define inf 0x3f3f3f3f3f

long long a[1010];
char f[10];

long long zma[10],zmi[10];

int main()
{
    int t,n,m;
    long long k;
    cin>>t;
    while(t--)
    {
            for(int i=0;i<10;i++)
            {
                    zma[i]=-1e18;
                    zmi[i]=1e18;
            }
            cin>>n>>m>>k;
            for(int i=1;i<=n;i++)
            {
                    cin>>a[i];
            }
                cin>>f;
            for(int i=1;i<=m;i++)
            {
                    for(int j=i-1;j>=0;j--)
                    {
                            long long x1,x2,now1,now2;
                            if(j>0)
                            {
                                    x1=zma[j-1];
                                    x2=zmi[j-1];
                            }
                            else
                            {
                                    x1=k;
                                    x2=k;
                            }

                            if(f[j]=='+')
                            {
                                    now1=x1+a[i];
                                    now2=x2+a[i];
                            }
                            else if(f[j]=='-')
                            {
                                    now2=x2-a[i];
                                    now1=x1-a[i];
                            }
                            else if(f[j]=='*')
                            {
                                    now1=x1*a[i];
                                    now2=x2*a[i];
                            }
                            else if(f[j]=='/')
                            {
                                    now1=x1/a[i];
                                    now2=x2/a[i];
                            }
                            if(now1>zma[j])
                                zma[j]=now1;
                            if(now1<zmi[j])
                                zmi[j]=now1;
                            if(now2>zma[j])
                                zma[j]=now2;
                            if(now2<zmi[j])
                                zmi[j]=now2;
                    }
            }
            for(int i=m+1;i<=n;i++)
            {
                    for(int j=m-1;j>=0;j--)
                    {
                            long long x1,x2,now1,now2;
                            if(j>0)
                            {
                                    x1=zma[j-1];
                                    x2=zmi[j-1];
                            }
                            else
                            {
                                    x1=k;
                                    x2=k;
                            }

                            if(f[j]=='+')
                            {
                                    now1=x1+a[i];
                                    now2=x2+a[i];
                            }
                            else if(f[j]=='-')
                            {
                                    now2=x2-a[i];
                                    now1=x1-a[i];
                            }
                            else if(f[j]=='*')
                            {
                                    now1=x1*a[i];
                                    now2=x2*a[i];
                            }
                            else if(f[j]=='/')
                            {
                                    now1=x1/a[i];
                                    now2=x2/a[i];
                            }
                            if(now1>zma[j])
                                zma[j]=now1;
                            if(now1<zmi[j])
                                zmi[j]=now1;
                            if(now2>zma[j])
                                zma[j]=now2;
                            if(now2<zmi[j])
                                zmi[j]=now2;
                    }
            }
            cout<<zma[m-1]<<endl;
    }
    return 0;
}

/*
100
5 5 1000
1000 1000 1000 1000 1000
*****
*/

G. Give Candies

题意

1
给n个小孩发糖果，总共有n个糖果，小孩按顺序排好，把糖果分发，不必每个小孩都有糖果，但是如果不是每个孩子都有糖果，那么只能是在后面的小孩没有糖果。问有多少种方案。

题解

就是往n个东西中间插任意个板子，所以最多能插n - 1个，所以答案为2^(n - 1) % p。但是n最大有1e5位数，所以要用小费马定理化简。

假如p是质数，且gcd(a,p)=1，那么

a^(p-1) ≡1（mod p）

我们可以利用费马小定理来简化幂模运算：由于a^(p-1)≡a^0≡1(mod p)，所以a^x(mod p)有循环节，长度为p-1，所以a^x≡a^(x%(p-1))(mod p)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=1e9+7;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
string s;
ll poww(ll b){
    ll ans=1,base=2;
    while(b){
        if(b&1)ans=(ans*base)%mod;
        base=(base*base)%mod;
        b/=2;
    }
    return ans;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int t;
    cin>>t;
    while(t--){
        cin>>s;
        int len=s.length();
        ll num=0;
        for(int i=0;i<len;i++){
            num=((num*10)+(s[i]-'0'))%(mod-1);
        }
        num-=1;
        cout<<poww(num)<<endl;
    }
    return 0;
}

H. String and Times

题意

求子串出现次数在k1=<num<=k2;

题解

https://blog.csdn.net/calabash_boy/article/details/77959704

抄了葫芦娃的这篇博客直接1A 太强了

1
2
3
4
5
恰好k次 = 至少k次 - 至少k+1次。答案转化为求至少出现k次的子串个数统计。构造好后缀数组以及很重要的Height数组之后。用一个k-1的窗子去滑动。窗子里边放着k-1个Height值（Height[ i+1 ]，Height[ i+2 ]，……，Height[ i+k ]），这样k-1个值就联系了k个后缀（SA[ i ]，SA[ i+1 ]，……，SA[ i+k ]），显然要求出这k-1个Height值的最小值，这个最小值就是这k个后缀的极大公共前缀了，假设是x，那么长度为1..x的前缀都在这个窗子里面出现了k次，也就是说他们都是符合答案的子串了。但是要考虑前边已经重复统计过了1..x中的一部分，考虑前一个窗子（Height[ i ]，Height[ i+1 ]，……，Height[ i+k-1 ]），讨论前面这个窗子的最小值y：1、y<x，那么说明上一个窗子的最小值一定是Height[ i ] ，因此上一个窗子统计了1..Height[ i ]部分，这一次需要统计Height[ i ]..x部分。2、y>x，那么就是说明前面窗子的极大公共前缀长度 比 这一个窗子的 极大公共前缀长，而这两个窗子有（i+1,i+2,，……,i+k-1）这k-2个元素是一样的。因此考虑所有的k个值（Height[ i ]，Height[ i+1 ]，……，Height[ i+k-1 ]，Height[ i+k ]），1..x必然是他们的公共前缀，那么由于y>x，前面一个窗子已经统计完了1..y的部分，1..x的部分被计算在前一个窗子里面了，这一次不需要计算，为了和上边一个式子统一起来，我们考虑Height[ i ]，显然有Height[ i ]>=y>x，进而有Height[ i ]>x。



因此结论是：用k-1的窗子从2开始滑动，维护窗子的最小值，然后每个窗子和刚刚移出窗子的那个Height作比较，如果min>Height，就统计min-Height。相反不统计。维护最小值用单调队列复杂度最低（priority_queue是nlogn，手写数组模拟是n）。构造后缀数组用倍增方法，复杂度是nlogn，因此整体复杂度是nlogn。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MaxN=1e5+100;
const int MAXN = MaxN;
ll cntA[MaxN],cntB[MaxN],tsa[MAXN],A[MAXN],B[MAXN];
ll sa[MAXN],Rank[MAXN],h[MAXN];
char ch[MAXN];
ll k1,k2;
struct Node{
	int val,index;
	Node(int val_,int index_):val(val_),index(index_){
	}
	bool operator < (const Node b)const{
		if (val==b.val){
			return b.index<index;
		}
		return b.val<val;
	}
};
priority_queue<Node>pq;
void GetSa(char *ch,ll *sa,ll *rank,ll n){

    for(int i=0;i<MaxN;i++)  cntA[i]=0;
    for(int i=1;i<=n;i++)   cntA[ch[i]]++;
    for(int i=1;i<=MaxN;i++) cntA[i]+=cntA[i-1];
    for(int i=n;i;i--)  sa[cntA[ch[i]]--]=i;
    rank[sa[1]]=1;
    for(int i=2;i<=n;i++){
        rank[sa[i]]=rank[sa[i-1]];
        if(ch[sa[i]]!=ch[sa[i-1]])  rank[sa[i]]++;
    }
    for(int l=1;rank[sa[n]]<n;l<<=1){
        for(int i=0;i<MaxN;i++)  cntA[i]=0;
        for(int i=0;i<MaxN;i++)  cntB[i]=0;
        for(int i=1;i<=n;i++){
            cntA[A[i]=rank[i]]++;
            cntB[B[i]=(i+l<=n)?rank[i+l]:0]++;
        }
        for(int i=1;i<MaxN;i++)   cntB[i]+=cntB[i-1];
        for(int i=n;i;i--)  tsa[cntB[B[i]]--]=i;
        for(int i=1;i<MaxN;i++)  cntA[i]+=cntA[i-1];
        for(int i=n;i;i--)  sa[cntA[A[tsa[i]]]--]=tsa[i];
        rank[sa[1]]=1;
        for(int i=2;i<=n;i++){
            rank[sa[i]]=rank[sa[i-1]];
            if(A[sa[i]]!=A[sa[i-1]] || B[sa[i]]!=B[sa[i-1]])    rank[sa[i]]++;
        }
    }
}

void GetHeight(char *ch,ll *sa,ll *rank,ll *height,ll n){

    GetSa(ch,sa,rank,n);
    for(int i=1,j=0;i<=n;i++){
        if(j)   j--;
        while(ch[i+j]==ch[sa[rank[i]-1]+j]) j++;
        height[rank[i]]=j;
    }
}
ll GetK(ll k,ll n){
    ll ans=0;
    k--;
    if(k==0){
        for(int i=1;i<=n;++i)   ans=ans+(n-sa[i]+1-h[i]);
        return ans;
    }
	while (!pq.empty())pq.pop();
	for (int i=2;i<=n;i++){
		while (!pq.empty()&&pq.top().index<i-k+1)pq.pop();
		pq.push(Node(h[i],i));
		if (i>k){
			int top = pq.top().val;
			int last = h[i-k];
			ans +=max(0,top-last);
		}
	}
    return ans;
}

void Run(){
    ll n,k;
    while(~scanf("%s",ch+1)){
        scanf("%lld%lld",&k1,&k2);
        n=strlen(ch+1);
        GetHeight(ch,sa,Rank,h,n);
        printf("%lld\n",GetK(k1,n)-GetK(k2+1,n));
    }
}
int main(){
    Run();
    return 0;
}

I. Save the Room

题意

有一个abc大小的长方体，你用112大小的长方体来填充，填充过程中，不能超出abc长方体的空间。问是否可以刚好填充。

题解

因为是1×1×2大小，所以以1×1为底面填充一定可以把底面填满，那么只需要考虑高就好啦，然后发现，高是二的倍数就可以刚好填充。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
string s;
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int a,b,c;
    while(cin>>a>>b>>c){
        if(a%2==0||b%2==0||c%2==0)cout<<"Yes"<<endl;
        else cout<<"No"<<endl;
    }
    return 0;
}

J. Participate in E-sports

题意

让你分别判断n或（n-1）*n/2是否是完全平方数。

题解

大数开方，可以二分或者牛顿迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
import java.math.BigInteger;
import java.util.Scanner;

public class Main{
	static BigInteger cal(BigInteger x){
        BigInteger l = BigInteger.ONE ;
        BigInteger r = x ;
        BigInteger temp = BigInteger.ZERO ;
        while(!l.equals(r)){
            BigInteger mid = (l.add(r)).divide(BigInteger.valueOf(2)) ;
            if(temp.compareTo(BigInteger.ZERO)!=0&&temp.compareTo(mid)==0){
                break ;
            }else{
                temp = mid ;
            }
            if(temp.compareTo(BigInteger.ZERO)==0){
                temp = mid ;
            }
            if(mid.multiply(mid).compareTo(x)==1){
                r=mid ;
            }else{
                l=mid ;
            }
        }
        if(l.multiply(l).compareTo(x)==1){
            l=l.subtract(BigInteger.ONE) ;
        }
        return l;
        
    }
	public static void main(String[] args) {
		int T;
		Scanner cin=new Scanner(System.in);
		T=cin.nextInt();
		BigInteger a = BigInteger.ZERO ;	
		BigInteger b =BigInteger.ZERO ;	
		BigInteger tmp = BigInteger.ZERO  ;
		boolean flag1=false,flag2=false;
		while((T--)>0) {
			flag1=false;
			flag2=false;
			a=cin.nextBigInteger();
			tmp=cal(a);
			if(a.equals(BigInteger.ONE)){
	             System.out.println("Arena of Valor");
	               continue;
			}
			if(a.equals(BigInteger.valueOf(2))){
		          System.out.println("Clash Royale");
	               continue;
			}
			if(tmp.multiply(tmp).equals(a)){
				flag1=true;
			}
			if(a.mod(BigInteger.valueOf(2)).equals(BigInteger.ZERO)){
				BigInteger tmp1 = a.divide(BigInteger.valueOf(2));
                BigInteger tmp2 = a.subtract(BigInteger.ONE);
                BigInteger t1 = cal(tmp1);
                if (t1.multiply(t1).equals(tmp1)) {
                    BigInteger t2 = cal(tmp2);
                    if (t2.multiply(t2).equals(tmp2)) {
                        flag2 = true;
                    }
                }
			}
			else{
			     BigInteger tmp1 = a.subtract(BigInteger.ONE).divide(BigInteger.valueOf(2));
	                BigInteger t1 = cal(tmp1);
	                if (t1.multiply(t1).equals(tmp1)) {
	                    if(flag1 == true) {
	                        flag2 = true;
	                    }
	                }	
			}
			if(flag1==true&&flag2==true) {
				System.out.println("Arena of Valor");
			}
			else if(flag1==true&&flag2==false) {
				System.out.println("Hearth Stone");
			}
			else if(flag1==false&&flag2==true) {
				System.out.println("Clash Royale");
			}
			else{
				System.out.println("League of Legends");
			}
		}
	}
}

K. Transport Ship

题意

每个物品的大小为v有2^c-1个 q次询问 问你当背包容量为s的时候有多少种可行方案

题解

多重二进制背包，把每个容量变成二进制表示 比如2^3-1=8-1=7=={1,2,4};正好三次

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pp pair<int,int>
const ll mod=1e9+7;
const int maxn=1e4+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int gcd(int a,int b){while(b){int t=a%b;a=b;b=t;}return a;}
int lcm(int a,int b){return a*b/gcd(a,b);}
ll dp[10010];
int v[20],c[20];
int main()
{
   /* std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);*/
    int t;
    scanf("%d",&t);
    while(t--){
        int n,q;
        scanf("%d%d",&n,&q);
        memset(dp,0,sizeof(dp));
        dp[0]=1;
        int cc,vv;
        for(int i=0;i<n;i++){
            scanf("%d%d",&vv,&cc);
            int bit=1;
            for(int j=0;j<cc;j++){
                for(int k=10000;k>=bit*vv;k--){
                    dp[k]=(dp[k]+dp[k-bit*vv])%mod;
                }
                bit*=2;
            }
        }
        while(q--){
            int k;
            scanf("%d",&k);
            printf("%lld\n",dp[k]);
        }
    }
    return 0;
}

L. Poor God Water

题意

有肉，鱼，巧克力三种食物，有几种禁忌，对于连续的三个食物，1.这三个食物不能都相同；2.若三种食物都有的情况，巧克力不能在中间；3.如果两边是巧克力，中间不能是肉或鱼，求方案数

题解

这题类似于AC自动机的POJ-2778-病毒串问题，把不能的禁忌当成坏的子串然后用ac自动机得出矩阵后进行矩阵快速幂

不过一开始ac自动机过不去，就得出十组数据搞进BM里面了后面矩阵优化一下直接300ms过去了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
#include <bits/stdc++.h>

using namespace std;
#define rep(i,a,n) for (long long i=a;i<n;i++)
#define per(i,a,n) for (long long i=n-1;i>=a;i--)
#define pb push_back
#define mp make_pair
#define all(x) (x).begin(),(x).end()
#define fi first
#define se second
#define SZ(x) ((long long)(x).size())
typedef vector<long long> VI;
typedef long long ll;
typedef pair<long long,long long> PII;
const ll mod=1e9+7;
ll powmod(ll a,ll b){
    ll res=1;
    a%=mod;
 //   assert(b>=0);
    for(;b;b>>=1)
    {
    if(b&1)
    res=res*a%mod;
    a=a*a%mod;
    }
    return res;
}
// head

long long _,n;
namespace linear_seq
{
    const long long N=10010;
    ll res[N],base[N],_c[N],_md[N];

    vector<long long> Md;
    void mul(ll *a,ll *b,long long k)
    {
        rep(i,0,k+k) _c[i]=0;
        rep(i,0,k) if (a[i]) rep(j,0,k)
            _c[i+j]=(_c[i+j]+a[i]*b[j])%mod;
        for (long long i=k+k-1;i>=k;i--) if (_c[i])
            rep(j,0,SZ(Md)) _c[i-k+Md[j]]=(_c[i-k+Md[j]]-_c[i]*_md[Md[j]])%mod;
        rep(i,0,k) a[i]=_c[i];
    }
    long long solve(ll n,VI a,VI b)
    { // a 系数 b 初值 b[n+1]=a[0]*b[n]+...
//        printf("%d\n",SZ(b));
        ll ans=0,pnt=0;
        long long k=SZ(a);
   //     assert(SZ(a)==SZ(b));
        rep(i,0,k) _md[k-1-i]=-a[i];_md[k]=1;
        Md.clear();
        rep(i,0,k) if (_md[i]!=0) Md.push_back(i);
        rep(i,0,k) res[i]=base[i]=0;
        res[0]=1;
        while ((1ll<<pnt)<=n) pnt++;
        for (long long p=pnt;p>=0;p--)
        {
            mul(res,res,k);
            if ((n>>p)&1)
            {
                for (long long i=k-1;i>=0;i--) res[i+1]=res[i];res[0]=0;
                rep(j,0,SZ(Md)) res[Md[j]]=(res[Md[j]]-res[k]*_md[Md[j]])%mod;
            }
        }
        rep(i,0,k) ans=(ans+res[i]*b[i])%mod;
        if (ans<0) ans+=mod;
        return ans;
    }
    VI BM(VI s)
    {
        VI C(1,1),B(1,1);
        long long L=0,m=1,b=1;
        rep(n,0,SZ(s))
        {
            ll d=0;
            rep(i,0,L+1) d=(d+(ll)C[i]*s[n-i])%mod;
            if (d==0) ++m;
            else if (2*L<=n)
            {
                VI T=C;
                ll c=mod-d*powmod(b,mod-2)%mod;
                while (SZ(C)<SZ(B)+m) C.pb(0);
                rep(i,0,SZ(B)) C[i+m]=(C[i+m]+c*B[i])%mod;
                L=n+1-L; B=T; b=d; m=1;
            }
            else
            {
                ll c=mod-d*powmod(b,mod-2)%mod;
                while (SZ(C)<SZ(B)+m) C.pb(0);
                rep(i,0,SZ(B)) C[i+m]=(C[i+m]+c*B[i])%mod;
                ++m;
            }
        }
        return C;
    }
    long long gao(VI a,ll n)
    {
        VI c=BM(a);
        c.erase(c.begin());
        rep(i,0,SZ(c)) c[i]=(mod-c[i])%mod;
        return solve(n,c,VI(a.begin(),a.begin()+SZ(c)));
    }
};

int main()
{
    int t;
    scanf("%d",&t);
    while(t--){
    scanf("%lld",&n);
       printf("%lld\n",linear_seq::gao(VI{3,9,20,46,106,244,560,1286,2956,6794},n-1));
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
#include<algorithm>
#include <iostream>
#include <stdlib.h>
#include <string.h>
#include  <stdio.h>
#include   <math.h>
#include   <time.h>
#include   <vector>
#include   <bitset>
#include    <queue>
#include      <map>
#include      <set>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=10*10+5;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
struct Matrix{
    unsigned long long mat[maxn][maxn];
    int n;
    Matrix(){}
    Matrix(int _n){
        n=_n;
        for(int i=0;i<n;i++)for(int j=0;j<n;j++)mat[i][j]=0;
    }
    Matrix operator *(const Matrix &b)const{
        Matrix ret=Matrix(n);
        for(int i=0;i<n;i++){
            for(int k=0;k<n;k++){
                if(mat[i][k])
                for(int j=0;j<n;j++){
                    ret.mat[i][j]+=(mat[i][k]*b.mat[k][j])%mod;
                    ret.mat[i][j]%=mod;
                }
            }
        }
        return ret;
    }
    unsigned long long pow_m(unsigned long long a,int n){
        unsigned long long ret=1,tmp=a;
        while(n){
            if(n&1)ret*=tmp;
            tmp*=tmp;
            n>>=1;
        }return ret;
    }
    Matrix pow_M(Matrix a,ll n){
        Matrix ret=Matrix(a.n);
        for(int i=0;i<a.n;i++)ret.mat[i][i]=1;
        Matrix tmp=a;
        while(n){
            if(n&1)ret=ret*tmp;
            tmp=tmp*tmp;
            n>>=1;
        }
        return ret;
    }
};
struct Trie{
    int next[maxn][3],fail[maxn],id['z'+1];
    bool end[maxn];
    int root,L;
    int newnode(){
        for(int i=0;i<3;++i)next[L][i]=-1;
        end[L++]=false;
        return L-1;
    }
    void init(){
        L=0;
        id['a']=0;id['b']=1;id['c']=2;
        root=newnode();
    }
    void insert(char buf[]){
        int len=strlen(buf);
        int now=root;
        for(int i=0;i<len;i++){
            if(next[now][id[buf[i]]]==-1)next[now][id[buf[i]]]=newnode();
            now=next[now][id[buf[i]]];
        }
        end[now]=true;
    }
    void build(){
        queue<int>Q;
        fail[root]=root;
        for(int i=0;i<3;i++)
            if(next[root][i]==-1)next[root][i]=root;
            else{
                fail[next[root][i]]=root;
                Q.push(next[root][i]);
            }
        while(!Q.empty()){
            int now=Q.front();
            Q.pop();
            if(end[fail[now]])end[now]=true;
            for(int i=0;i<3;i++)
                if(next[now][i]==-1)
                    next[now][i]=next[fail[now]][i];
                else{
                    fail[next[now][i]]=next[fail[now]][i];
                    Q.push(next[now][i]);
                }
        }
    }
    Matrix getMatrix(){
        Matrix ret=Matrix(L);
        for(int i=0;i<L;i++){
            for(int j=0;j<3;j++){
                if(end[next[i][j]]==false&&end[i]==false)
                    ret.mat[i][next[i][j]]++;
            }
        }
        return ret;
    }

};
Trie ac;
char buf[9][4]={"aaa","bbb","ccc","acb","bca","cac","cbc"};
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);

    ac.init();
    for(int i=0;i<7;i++){
        ac.insert(buf[i]);
    }
    ac.build();
    int t;
    cin>>t;
    Matrix mat=ac.getMatrix();
    while(t--){
        ll L;
        cin>>L;

        Matrix matt=mat.pow_M(mat,L);
        ll ans=0;
        for(int i=0;i<matt.n;i++){
            ans=(ans+matt.mat[0][i])%mod;
        }
        cout<<ans<<endl;
    }
    return 0;
}

Diposting di | Edited on

传送门

A.HDU6438 Buy and Resell

题意

给你N天N个价格,每天都可以从1.买入一个,2.卖出一个,3.什么都不做,求最高获利</br>
低买高卖问题,这题与其他的差距就是要在满足获利最多的情况下,买卖次数最小;

思路

手算一下发现价格具有传递性;例如数据是1,5,9;
5的时候买入1赚了4;9的时候买入5赚了4;相当于直接把5当成跳板直接9的时候买1;然后再把中间的5当成没有买过的;</br>
建立一个小根堆(优先队列);把当前遇到的天数的价钱放入,然后对于第i天;</br>
1.如果新天数的价钱比堆顶小;说明交易亏本,直接丢入堆中;
2.如果价钱高说明有赚头;
2.1.如果堆顶的是已经跟之前的交易过的,那相当于当前天和之前的那个交易,然后堆顶的变成没有交易的;继续插入;交易次数不变
2.2否则直接交易,交易次数+2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f;
int a[maxn];
struct node{
    int id;
    int money;
    bool has;
    node(int id,int money,bool has):id(id),money(money),has(has){}
    bool friend operator <(node a,node b){
        if(a.money==b.money)return a.has<b.has;
        return a.money>b.money;
    }
};
int flag[maxn];
int used[maxn];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int t;
    cin>>t;
    while(t--){
        int n;
        cin>>n;
        ll ans=0;
        ll cnt=0;
        memset(flag,0,sizeof(flag));
        memset(used,-1,sizeof(used));
        for(int i=0;i<n;i++)cin>>a[i];
        priority_queue<node>pq;
        for(int i=0;i<n;i++){
            if(pq.empty())pq.push(node(i,a[i],0));
            else{
                node now=pq.top();
                if(now.money>=a[i])pq.push(node(i,a[i],0));
                else{
                    pq.pop();
                    if(flag[now.id]){
                        ans+=a[i]-now.money;
                        flag[i]=1;flag[now.id]=0;
                        used[i]=used[now.id];
                        used[now.id]=-1;
                        pq.push(node(i,a[i],1));
                        pq.push(node(now.id,a[now.id],0));
                    }
                    else{
                        ans+=a[i]-now.money;
                        cnt+=2;
                        flag[i]=1;flag[now.id]=1;
                        used[i]=now.id;
                        pq.push(node(i,a[i],1));
                    }
                }
            }
        }
        cout<<ans<<" "<<cnt<<endl;
    }
    return 0;
}

C.HDU6440 Dream

题意

对一个质数P，对小于P的非负数定义一种乘法和加法运算，使得其满足封闭性，且对于存在一个数q使得{qk|0< k< p}

思路

费马小定理,比赛随便迷一样的试了一下就A了,自己也不知道怎么解释…

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=1e5+50;
const ll inf=0x3f3f3f3f3f3f;
int n;
int vis[maxn];
int size[maxn];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int t;
    cin>>t;
    while(t--){
        int p;
        cin>>p;
        for(int i=0;i<p;i++){
            cout<<i;
            for(int j=1;j<p;j++){
                cout<<" "<<(i+j)%p;
            }
            cout<<endl;
        }

        for(int i=0;i<p;i++){
            cout<<0;
            for(int j=1;j<p;j++){
                cout<<" "<<(i*j)%p;
            }
            cout<<endl;
        }

    }
    return 0;
}

D.HDU6441 Find Integer

题意

题意：已知a^n+b^n=c^n，给出n和a，求b，c，如果无解输出−1。

思路

费马大定理

  1. a^n+b^n=c^n，n>2时无解。
  2. 当a为奇数时，
    a=2⋅k+1
    c=k^2+(k+1)^2
    b=c−1
    3.当 a 为偶数
    a=2∗k+2
    c=1+(k+1)^2
    b=c−2
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    #include<bits/stdc++.h>
    using namespace std;
    typedef long long ll;
    const ll mod=998244353;
    const int maxn=3e6+50;
    const ll inf=0x3f3f3f3f3f3f;

    int main()
    {
        //std::ios::sync_with_stdio(false);
       // std::cin.tie(0);
        //std::cout.tie(0);
        int t;
        scanf("%d",&t);
        while(t--){
            ll n,a;
            scanf("%lld%lld",&n,&a);
            if(n==0){
                printf("-1 -1\n");
            }
            else if(n==1){
                printf("1 %lld\n",a+1);
            }
            else if(n==2)
                {
                    if(a&1){
                        printf("%lld %lld\n",a*a/2,a*a/2+1);
                    }
                    else{
                        printf("%lld %lld\n",(a/2)*(a/2)-1,(a/2)*(a/2)+1);
                    }
                }
            else{
                printf("-1 -1\n");
            }
        }
        return 0;
    }

I.HDU6446 Tree and Permutation

题意

题意：给你一颗树，然后让你求n！种序列中，所以得序列和，序列和定义为：A1,A2,A3……AN=A1A2+A2A3+…….An-1An

思路

首先，对于题目给出的n-1条边，我们可以这样考虑，去掉这条边后，将树分成了两部分，一部分有M个节点，另一部分有（N-M）个节点，所以我们必须在这两块中任意选择一个节点才会进过这条边，所以，有N × M× 2 中选择，然后又N！个序列所以对于E这条边，一共又2×N×M×（N-1）！×L的贡献。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=1e5+50;
const ll inf=0x3f3f3f3f3f3f;
int n;
int vis[maxn];
int size[maxn];
struct Edge{
    int to;
    int s;
    int t;
    int l;
    Edge(int to,int s,int t,int l):to(to),s(s),t(t),l(l){}
};
ll f[maxn];
int init(){
    f[0]=1;f[1]=1;
    for(int i=2;i<=100000;i++)f[i]=(f[i-1]*i)%mod;
}
ll ans;
vector<Edge>G[maxn];
void dfs(int u){
    vis[u]=1;
    int cnt=1;
    for(int i=0;i<G[u].size();i++){
        Edge &e=G[u][i];
        if(vis[e.to]==0){
            dfs(e.to);
            ll tmp=size[e.to];
            tmp=tmp*(n-tmp)%mod;
            tmp=tmp*2%mod;
            tmp=tmp*e.l%mod;
            tmp=tmp*f[n-1]%mod;
            ans+=tmp;
            ans%=mod;
            cnt+=size[e.to];
        }
    }
    size[u]=cnt;
}

int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int t;
    init();
    while(cin>>n){
        for(int i=0;i<=n;i++)G[i].clear();
        for(int i=0;i<=n;i++)size[i]=0,vis[i]=0;
        ans=0;
        for(int i=0;i<n-1;i++){
            ll x,y,l;
            cin>>x>>y>>l;
            G[x].push_back(Edge(y,x,y,l));
            G[y].push_back(Edge(x,x,y,l));
        }
        dfs(1);
        cout<<ans<<endl;
    }
    return 0;
}

J.HDU6447 YJJ’s Salesman

题意

题意：一个地图,里面有最多1e5个村庄,YJJ从0,0开始走,只能向左,下,左下走,如果向左下走进一个村庄那就能获得这个村庄的价值;求最大价值;从(0,0)到(n,n);
数据范围1e9！数组装不下

思路

首先题意是求最大值,最基本的DP模型是三个方向的最大值;但是复杂度会爆炸而且也开不了那么大的数组;
1.离散化坐标;因为1e9的坐标范围太大数组装不下,但是只有1e5的村庄,所以可以把1e9离散化到1e5里面;</br>
2.每次搜索前面的最大值;利用树状数组搜索到当前位置的J坐标之前的最大值然后加上当前值再添加进树状数组</br>
比赛的时候离散完,想吧坐标压缩成一维的可是没想到办法所以凉凉了,其实这题不用压缩直接按照x的坐标从小到大排序,然后按照同一行从大到小排序就行了;

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e5+50;
const int maxm=1e5+50;
const ll inf=0x3f3f3f3f3f3f;
int N;
struct node{
    int x,y,value;
};
int cmp(node a,node b){
    if(a.x==b.x)return a.y>b.y;
    return a.x<b.x;
}
int c[maxm];
inline int lowbit(int x){return x&(-x);}
void update(int x,int p){
    for(int i=x;i<maxn;i+=lowbit(i)){
        c[i]=max(c[i],p);
    }
}
int query(int x){
    int ma=0;
    for(int i=x;i>0;i-=lowbit(i)){ma=max(ma,c[i]);}
    return ma;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int t;
    cin>>t;
    while(t--){
        int n;
        cin>>n;
        vector<node>ve;
        vector<int>k;
        k.push_back(-1);
        memset(c,0,sizeof(c));
        for(int i=0;i<n;i++){
            node a;
            cin>>a.x>>a.y>>a.value;
            ve.push_back(a);
            k.push_back(a.y);
        }
        sort(k.begin(),k.end());
        sort(ve.begin(),ve.end(),cmp);
        k.erase(unique(k.begin(),k.end()),k.end());
        N=k.size();
        int anw=0;
        for(int i=0;i<n;i++){
            int ans=lower_bound(k.begin(),k.end(),ve[i].y)-k.begin();
            int cnt=query(ans-1);
            cnt+=ve[i].value;
            update(ans,cnt);
            anw=max(anw,cnt);
        }
        cout<<anw<<endl;
    }
    return 0;
}

Diposting di | Edited on

传送门

付队！

B.Baby Bites (签到模拟)

按照题意模拟就行了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
int a[maxn];
string s;
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n;
    cin>>n;
    int st=-1;
    int ed=-1;
    int isok=0;
    for(int i=1;i<=n;i++){
        cin>>s;
        if(s[0]=='m')a[i]=i;
        else{
            if(st==-1)st=i;
            int len=s.size();
            int num=0;
            for(int j=0;j<len;j++)num=num*10+s[j]-'0';
            a[i]=num;
            if(a[i]==0){
                ed=1;
            }
        }
    }
    for(int i=1;i<=n;i++){
        if(a[i]!=i){cout<<"something is fishy"<<endl;return 0;}

    }
    cout<<"makes sense"<<endl;
    return 0;
}

C.Code Cleanups (贪心)

题意

A[i]天会出现一个垃圾，如果不清扫每天都会+1个垃圾.不能超过20个垃圾不清扫，问你最少清扫几次

题解

直接贪心取就完事了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int a[maxn];
int vis[maxn];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)cin>>a[i],vis[a[i]]=1;
    int ans=0,now=0,cnt=0;
    for(int i=1;i<=365;i++){
        now+=cnt;
        if(now>=20)ans++,now=cnt=0;
        if(vis[i])cnt++;
    }
    if(now||cnt)ans++;
    cout<<ans<<endl;
    return 0;
}

E.Explosion Exploit (记忆化搜索)

题意

给定N个自己人，M个敌人。以及每个人的血量ai。系统一共发起K次攻击，每次随机选择一个人物进行攻击，被攻击后血量少1，血量为0的不再考虑。问最后敌人都被杀死的概率。 （N,M<=5 ,ai<=6,K<=100）

题解

用位数模拟血量的人数,最多12位,所以数组开不下，只能用map储存,保存每个血量/国营的人数，概率就是，射中这个人的射中这个人的概率*射中这个人能全部杀掉的概率；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e5+50;
const int logmaxn=20;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
map<ll,double>mp;
ll a[2][8];

int n,m,d;
ll get(){
    ll ans=0;
    for(int i=1;i<=6;i++)ans=ans*10+a[1][i];
    for(int i=1;i<=6;i++)ans=ans*10+a[0][i];
    return ans;
}
double dfs(ll sta,int num){
    if(mp.count(sta))return mp[sta];
    if(sta<1000000)return 1;
    if(num==0)return 0;
    int sum=0;
    for(int i=0;i<2;i++)for(int j=1;j<=6;j++)sum+=a[i][j];
    double ans=0;
    for(int i=0;i<2;i++)
    for(int j=1;j<=6;j++){
        if(!a[i][j])continue;
        a[i][j]--;a[i][j-1]++;
        ll nex=get();
        double res=dfs(nex,num-1);
        a[i][j]++;a[i][j-1]--;
        ans+=(double)(a[i][j]*1.0/sum*1.0)*res*1.0;
    }
    mp[sta]=ans;
    return ans;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    cin>>n>>m>>d;
    for(int i=0;i<2;i++){
        int k=(i==0?n:m);
        for(int j=0;j<k;j++){
            int p;cin>>p;a[i][p]++;
        }
    }
    cout<<fixed<<setprecision(8)<<dfs(get(),d)<<endl;
    return 0;
}

H.House Lawn ()

solve by 许老师

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#include<bits/stdc++.h>
#define db double
#define ll long long
using namespace std;
const int maxn=1e6+6,inf=1e9;
char str[1005];
struct node
{
	char s[65];
	int id,p;
	bool operator<(const node&t)const
	{
		if(p==t.p)return id<t.id;
		return p<t.p;
	}
}a[105];
void gao(int cur,int &pri,int &c,int &t,int &r)
{
	int n=strlen(str),i=0;
	pri=c=t=r=0;
	while(str[i]!=',')i++;
	i++;
	while(str[i]!=',')
	pri=pri*10+str[i++]-'0';i++;
	while(str[i]!=',')
	c=c*10+str[i++]-'0';i++;
	while(str[i]!=',')
	t=t*10+str[i++]-'0';i++;
	while(i<n)
	r=r*10+str[i++]-'0'; 
}
int main()
{
	int e,m,pri,c,t,r,v,n=10080,cnt=0;
	cin>>e>>m;
	getchar();
	for(int i=1;i<=m;i++)
	{
		gets(str);
		gao(i,pri,c,t,r);
		v=n/(t+r)*t*c;
		if(v<e)
		{
			int tmp=n%(t+r);
			db v1=(db(e)-v)/c,v2=tmp-v1;
			if(v1<=(db)t)
			if(v1*r<=v2*t)v=e;
		}
		if(v>=e)
		{
			a[++cnt].p=pri; a[cnt].id=i;
			int len=strlen(str),j=0;
			while(str[j]!=',')
			a[cnt].s[j]=str[j],j++;
			a[cnt].s[j]='\0';
		}
	}
	sort(a+1,a+1+cnt);
	if(cnt==0)puts("no such mower");
	else
	{
		int i=1;
		while(1)
		{
			printf("%s\n",a[i++].s);
			if(i>cnt||a[i].p>a[i-1].p)break;	
		}
	}
}

I.Intergalactic Bidding (高精度)

题意

给出N个高精度数，表示N个人对应的数字，满足每个人的数字大于等于前面一个人的两倍，以及S。 输出winners，一个人是winner，当且仅当他存在一个集合里，这个集合是和是S。

题解

首先第一眼是背包问题，但是发现这个数字太大没办法开数组背包；于是注意到两倍这个关系

模拟一下二进制,从后往前，一个数字从后往前，寻找她的二进制位的过程你就会知道怎么做了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
string s;
int cmp(string a,string b){
    if(a.length()>b.length())return true;
    else if(a.length()<b.length())return false;
    else return a>=b;
}
bool vis[1100];
struct node{
    string name;
    string money;
}my[1100];
bool cmpp(node a,node b){
    if(a.money.size()>b.money.size())return true;
    else if(a.money.size()<b.money.size())return false;
    else return a.money>b.money;
}
string sub(string a,string b){
    string ans="";
    reverse(a.begin(),a.end());
    reverse(b.begin(),b.end());
    int len1=a.length(),len2=b.length();
    int pre=0;
    for(int i=0;i<len2;i++){
        int now=a[i]-b[i];
        if(now<0)a[i+1]--,now=10+now;
        ans+=(char)(now+'0');
    }
    for(int i=len2;i<len1;i++){
        int num=a[i]-'0';
        if(num<0){
            num+=10;
            a[i+1]--;
        }
        ans+=(char)(num+'0');
    }
    while(ans.size()>1&&ans.back()=='0')ans.pop_back();
    reverse(ans.begin(),ans.end());
    return ans;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n;
    cin>>n;
    cin>>s;
    for(int i=1;i<=n;i++){
        cin>>my[i].name>>my[i].money;
    }
    int num=0;
    sort(my+1,my+1+n,cmpp);
    for(int i=1;i<=n;i++){
        if(cmp(s,my[i].money)){
            s=sub(s,my[i].money);
            vis[i]=1;
            num++;
        }
    }
    if(s=="0"){
        cout<<num<<endl;
        for(int i=1;i<=n;i++){
            if(vis[i])cout<<my[i].name<<endl;
        }
    }
    else{
        cout<<"0"<<endl;
    }
    return 0;
}

J.Jumbled String (构造题)

题意

solve by 付队

给你00，01，10，11子序列的数量a，b，c，d。 让你根据信息还原一个字符串

题意

由00和11的数量，我们可以得到字符串中0和1的数量x和y，然后取凑即可， 注意00数量为0时，x可能为0，也可能为1，其它情况下，x唯一； y同理。

假设得到了x，y。 我们可以试着构造一个形如11111…0001000….1111的串，即中间可以夹杂一个1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include<bits/stdc++.h>
#define ll long long
#define rep(i,a,b) for(int i=a;i<=b;i++)
using namespace std;
const int maxn=3010;
const int Mod=1e9+7;
map<int,int>mp;
bool check(int A,int D,int B,int C)// 0,1
{
    if(1LL*A*D!=1LL*B+C) return false;
    if(A==0&&B==0&&C==0){
        rep(i,1,D) putchar('1'); return true;
    }
    if(D==0&&B==0&&C==0){
        rep(i,1,A) putchar('0'); return true;
    }
    int num=B/A,rem=B%A;
    rep(i,1,D-num-(rem!=0)) putchar('1');
    rep(i,1,A) {
        putchar('0');
        if(rem==i) putchar('1');
    }
    rep(i,1,num) putchar('1');
    return true;
}
int main()
{
    int A,B,C,D;
    rep(i,1,44721){
       int tmp;
       if(i&1) tmp=(i-1)/2*i;
       else tmp=i/2*(i-1);
       mp[tmp]=i;
    }
    scanf("%d%d%d%d",&A,&B,&C,&D);
    if(mp[A]==0) return puts("impossible"),0;
    if(mp[D]==0) return puts("impossible"),0;
    if(check(mp[A],mp[D],B,C)) return 0;
    if(A==0&&check(0,mp[D],B,C)) return 0;
    if(D==0&&check(mp[A],0,B,C)) return 0;
    if(A==0&&D==0&&check(0,0,B,C)) return 0;
    puts("impossible");
    return 0;
}

K.King’s Colors (容斥)

题意

给你N，K，一棵大小为N的树，求刚好染K种色，而且相邻边颜色不同的方案数。

题解

solve by 付队

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include<bits/stdc++.h>
#define ll long long
#define rep(i,a,b) for(int i=a;i<=b;i++)
using namespace std;
const int maxn=3010;
const int Mod=1e9+7;
int C[maxn][maxn],N,K,ans;
int qpow(int a,int x)
{
    int res=1; while(x){
        if(x&1) res=(ll)res*a%Mod;
        a=(ll)a*a%Mod; x>>=1;
    } return res;
}
int main()
{
    rep(i,0,2500) C[i][0]=C[i][i]=1;
    rep(i,1,2500)
      rep(j,1,i) C[i][j]=(C[i-1][j-1]+C[i-1][j])%Mod;
     scanf("%d%d",&N,&K);
    rep(i,2,N){
        int u; scanf("%d",&u);
    }
    for(int i=K;i>=2;i--){
        if((K-i)%2==0){
            (ans+=(ll)i*qpow(i-1,N-1)%Mod*C[K][i]%Mod)%=Mod;
        }
        else {
            ans=((ans-(ll)i*qpow(i-1,N-1)%Mod*C[K][i]%Mod)%Mod+Mod)%Mod;
        }
    }
    printf("%d\n",ans);
    return 0;
}

Diposting di | Edited on

传送门

付队！

许老师！

B.Marbles （nim博弈）

题意

一个棋盘n个点,每次可以把一个棋子移动到(x-d,y) or (x,y-d) or (x-d,y-d) 把其中一个棋子移动到(0,0)的人就胜利

问先手能否必胜

思路

我非常喜欢的一题，一开始看到题面第一反应我操nim博弈煞笔题,然后傻逼一样得写了 判断到全部到（0，0)就赢的博弈，后面发现我想错了，我写的是相当于把全部石子取完的博弈，而这题只要把其中一堆石子取完就赢了，所以不正确，还是许老师厉害，把题意转换一下，题目开始是到(0,0)就赢，那什么情况下肯定输呢，那就是到(1,2) (2,1)这种死局的情况，每个人肯定都不想发生这种情况，于是我们就把题目转化成 把石子取到(1,2) （2,1）这种奇异态，而如果一个人面临这种局面那就是稳输的，于是我们把(1,2)这种状态构造成取完，而后面一个人面临一个取完（只有必败态的）时候那他就必输，所以这题就变成把N堆石子取成必输态的NIM博弈了，注意要特判先手直接赢的情况

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e6+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int sg[110][110];
int flag[500];
void init(){
    for(int i=1;i<=100;i++)sg[i][0]=sg[0][i]=sg[i][i]=0;
    for(int i=1;i<=100;i++){
        for(int j=1;j<=100;j++){
            if(i==j)continue;
            memset(flag,0,sizeof(flag));
            for(int k=1;k<i;k++)if(k!=j)flag[sg[k][j]]=1;
            for(int k=1;k<j;k++)if(k!=i)flag[sg[i][k]]=1;
            for(int k=1;k<min(i,j);k++)
                if(i-k!=j-k)flag[sg[i-k][j-k]]=1;
            for(int k=0;k<500;k++){
                if(flag[k]==0){sg[i][j]=k;break;}
            }
        }
    }
}

int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n;
    cin>>n;
    init();
    int f=0;
    int ans=0;
    while(n--){
        int a,b;
        cin>>a>>b;
        ans^=sg[a][b];
        if(a==b)f=1;
    }
    if(f||ans)cout<<"Y"<<endl;
    else cout<<"N"<<endl;
    return 0;
}

D.Unraveling Monty Hall（水题）

判断不是1的个数就行，大早上读题读得我怀疑人生

1
2
3
4
5
6
7
8
9
    int n;
    cin>>n;
    int ans=0;
    while(n--){
        int a;cin>>a;ans+=(a==1)?0:1;
    }
    cout<<ans<<endl;
    return 0;
}

E.Enigma (模拟)

题意

给你两个字符串s,t让判断前strlen(t)中的s有多少个是T中没有的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e2+50;
const ll inf=1e10;
const double eps=1e-5;

int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    string s;
    string t;
    cin>>s>>t;int ans=0;
    int len=s.size();int len1=t.size();
    for(int i=0;i<len-len1+1;i++){
        bool flag=1;
        for(int j=0;j<len1;j++)if(t[j]==s[i+j])flag=0;
        ans+=flag;
    }
    cout<<ans<<endl;
    return 0;
}

F.Music Festival (线段树/线段数组) （待补）

题意

有N个舞台(N<10)，第i个舞台有Mi首歌(M总和<1000)，给出每首歌的起始时间s，和终止时间t，以及价值val； 我们听完一首歌可以任意瞬移到另外的舞台，即不考虑时间边界。现在让你选择一种方案，使得每个舞台都至少听了一首歌，求最大价值。

题解

G.Gasoline (二分网络流)

题意

有p个加油站，r个油田，给出每个加油站需要的油以及每个油田库存的油，有C条加油站到油田的带权路，求每个加油站都能加满油时的最长的运输时间的最小值。

题解

二分最小值，建图，套网络流模板完事

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e5+50;
const ll inf=1e10;
const ll INF = 1000000000;
const double eps=1e-5;
struct Edge {
  int from, to;
  ll cap, flow;
};

struct Dinic {
  int n, m, s, t;
  vector<Edge> edges;    // 边数的两倍
  vector<int> G[maxn];   // 邻接表，G[i][j]表示结点i的第j条边在e数组中的序号
  bool vis[maxn];         // BFS使用
  int d[maxn];           // 从起点到i的距离
  int cur[maxn];        // 当前弧指针

  void ClearAll(int n) {
    for(int i = 0; i < n; i++) G[i].clear();
    edges.clear();
  }

  void ClearFlow() {
    for(int i = 0; i < edges.size(); i++) edges[i].flow = 0;
  }

  void AddEdge(int from, int to, ll cap) {
    edges.push_back((Edge){from, to, cap, 0});
    edges.push_back((Edge){to, from, 0, 0});
    m = edges.size();
    G[from].push_back(m-2);
    G[to].push_back(m-1);
  }

  bool BFS() {
    memset(vis, 0, sizeof(vis));
    queue<int> Q;
    Q.push(s);
    vis[s] = 1;
    d[s] = 0;
    while(!Q.empty()) {
      int x = Q.front(); Q.pop();
      for(int i = 0; i < G[x].size(); i++) {
        Edge& e = edges[G[x][i]];
        if(!vis[e.to] && e.cap > e.flow) {
          vis[e.to] = 1;
          d[e.to] = d[x] + 1;
          Q.push(e.to);
        }
      }
    }
    return vis[t];
  }

  int DFS(int x, ll a) {
    if(x == t || a == 0) return a;
    int flow = 0, f;
    for(int& i = cur[x]; i < G[x].size(); i++) {
      Edge& e = edges[G[x][i]];
      if(d[x] + 1 == d[e.to] && (f = DFS(e.to, min(a, e.cap-e.flow))) > 0) {
        e.flow += f;
        edges[G[x][i]^1].flow -= f;
        flow += f;
        a -= f;
        if(a == 0) break;
      }
    }
    return flow;
  }

  ll Maxflow(int s, int t) {
    this->s = s; this->t = t;
    int flow = 0;
    while(BFS()) {
      memset(cur, 0, sizeof(cur));
      flow += DFS(s, INF);
    }
    return flow;
  }

  vector<int> Mincut() { // call this after maxflow
    vector<int> ans;
    for(int i = 0; i < edges.size(); i++) {
      Edge& e = edges[i];
      if(vis[e.from] && !vis[e.to] && e.cap > 0) ans.push_back(i);
    }
    return ans;
  }

  void Reduce() {
    for(int i = 0; i < edges.size(); i++) edges[i].cap -= edges[i].flow;
  }
};

Dinic g;

int a[maxn],b[maxn],u[maxn],v[maxn],w[maxn];
int p,r,c,sum=0;
int S,T;
bool isok(int x){
    g.ClearAll(T+1);
    for(int i=1;i<=p;i++)g.AddEdge(S,i,a[i]);
    for(int i=1;i<=r;i++)g.AddEdge(p+i,T,b[i]);
    for(int i=1;i<=c;i++)if(w[i]<=x)g.AddEdge(u[i],p+v[i],inf);
    ll res=g.Maxflow(S,T);
    if(res==sum)return true;
    else return false;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);

    cin>>p>>r>>c;
    S=0,T=p+r+1;
    for(int i=1;i<=p;i++)cin>>a[i],sum+=a[i];
    for(int i=1;i<=r;i++)cin>>b[i];
    for(int i=1;i<=c;i++)cin>>u[i]>>v[i]>>w[i];
    int L=0,R=1e7,ans=-1;
    while(L<=R){
        int mid=(L+R)/2;
        if(isok(mid))R=mid-1,ans=mid;
        else L=mid+1;
    }
    if(ans==-1)cout<<-1<<endl;
    else cout<<ans<<endl;
    return 0;
}

I.Switches (模拟)

题意

给定N个灯，以及开始状态。M个开关集合，每次使用一个开关，这个集合的状态会改变。 现在一次按1到M个开关，即1，2，3，…M ,1, 2,… 问第几次会全部关掉。

思路

直接模拟咯，用bitset表示灯的状态

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e5+50;
const ll inf=1e10;
const ll INF = 1000000000;
const double eps=1e-5;
bitset<1010>b[1100],c;

int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n,m,k,x;
    cin>>n>>m>>k;
    for(int i=0;i<k;i++)cin>>x,c.set(x);
    for(int i=1;i<=n;i++){
        cin>>k;while(k--)cin>>x,b[i].set(x);
    }
    for(int i=1;i<=n;i++){
        c^=b[i];
        if(c.count()==0){
            cout<<i<<endl;return 0;
        }
    }
    for(int i=1;i<=n;i++){
        c^=b[i];
        if(c.count()==0){
            cout<<i+n<<endl;
            return 0;
        }
    }
    cout<<-1<<endl;
    return 0;
}

L.Subway Lines (树剖) （待补）

题意

给一棵树，询问两条路径上公共点的个数。