个人模板整理

Diposting di | Edited on

数据结构

字符串处理

KMP

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
/*
* next[] 的含义：x[i-next[i]...i-1]=x[0...next[i]-1] 
* next[i] 为满足 x[i-z...i-1]=x[0...z-1] 的最大 z 值（就是 x 的自身匹配）
*/ 
void kmp_pre(char x[],int m,int next[]){
    int i,j;
    j=next[0]=-1;
    i=0;
    while(i<m){
        while(-1!=j&&x[i]!=x[j])j=next[j];
        next[++i]=++j;
    }
}
/* 
 * kmpNext[i] 的意思:next'[i]=next[next[...[next[i]]]](直到 next'[i]<0 或者 x[next'[i]]!=x[i])
 * 这样的预处理可以快一些 
 */ 
void preKmp(char x[],int m,int kmpNext[]){
    int i,j;
    j=kmpNext[0]=-1;
    i=0;
    while(i<m){
        while(-1!=j && x[i]!=x[j])j=kmpNext[j];
        if(x[++i]==x[++j])kmpNext[i]=kmpNext[j];
        else kmpNext[i]=j;
    }
}
/*
返回x 在 y 中出现的次数，可以重叠
*/
int mynext[maxn];
int kmp(char x[],int m,char y[],int n){ // x是模式串 ，y是主串
    int i,j;
    int ans=0;
    kmp_pre(x,m,mynext);
    i=j=0;
    while(i<n){
        while(-1!=j&&y[i]!=y[j])j=mynext[j];
        i++;j++;
        if(j>=m){
            ans++;
            j=mynext[j];
        }
    }
    return ans;
}

e-KMP

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/*
 * 扩展KMP算法
 */
// next[i]:x[i...m-1] 与x[0...m-1]的最长公共前缀
void pre_EKMP(char x[],int m,int next[]){
    next[0]=m;
    int j=0;
    while(j+1<m && x[j] == x[j+1])j++;
    next[1]=j;
    int k=1;
    for(int i=2;i<m;i++){
        int p=next[k]+k-1;
        int L=next[i-k];
        if(i+L < p+1)next[i]=L;
        else{
            j=max(0,p-i+1);
            while( i+j < m && x[i+j] == x[j])j++;
            next[i]=j;
            k=i;
        }
    }
}
void EKMP(char x[],int m,int y[],int n,int next[],int extend[]){
    pre_EKMP(x,m,next);
    int j=0;
    while(j < n && j < m && x[j] == y[j])j++;
    extend[0]=j;
    int k=0;
    for(int i = 1;i < n;i++){
        int p = extend[k]+k-1;
        int L=next[i-k];
        if(i+L < p+1)extend[i]=L;
        else{
            j=max(0,p-i+1);
            while(i+j < n && j < m && y[i+j] == x[j])j++;
            extend[i]=j;
            k=i;
        }
    }
}

Z-算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
//求每个位置匹配前缀的长度的最大值  s[0…z[i]-1]=s[i…i+z[i]-1]
vector<int> ZF(const string &s){
    vector<int>z(s.size());
    int l=0,r=1;
    for(int i=1;i<(int)s.size();i++){
        if(r>i)z[i]=min(z[i-l],r-i);
        if(z[i]+i>=r){
            l=i,r=z[i]+i;
            while(r<(int)s.size()&&s[r]==s[r-l])r++;
            z[i]=r-l;
        }
    }
    return z;
}

最大最小表达式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
int getminmax(bool flag,string s){
    int i=0,j=1,k=0;
    int len=s.length();
    while(i<len&&j<len&&k<len){
        int t=s[(i+k)%len]-s[(j+k)%len];
        if(t==0)k++;
        else{
            if(!flag){
                if(t>0)i=i+k+1;
                else   j=j+k+1;
            }
            else{
                if(t>0)j=j+k+1;
                else   i=i+k+1;
            }
            if(i==j)j++;
            k=0;
        }
    }
    return i<j?i:j;
}

Manacher

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
char Ma[maxn*2];
int Mp[maxn*2]; ///需要-1才是最长回文的长度
int Manacher(char s[],int len){
    int l=0,ans=0;
    Ma[l++]='$';
    Ma[l++]='#';
    for(int i=0;i<len;i++){
        Ma[l++]=s[i];
        Ma[l++]='#';
    }
    Ma[l]=0;
    int mx=0,id=0;
    for(int i=0;i<l;i++){
        Mp[i]=mx>i?min(Mp[2*id-i],mx-i):1;
        while(Ma[i+Mp[i]]==Ma[i-Mp[i]])Mp[i]++;
        if(i+Mp[i]>mx){
            mx=i+Mp[i];
            id=i;
        }
        ans+=Mp[i]/2;
    }
    return ans;///计算共有多少回文串
}
/* 
 * abaaba
 * i: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 
 * Ma[i]: $ # a # b # a # a # b # a # 
 * Mp[i]: 1 1 2 1 4 1 2 7 2 1 4 1 2 1 
 */

Manacher返回最长回文串

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
string Manacher(string s) {
    // Insert '#'
    string t = "$#";
    for (int i = 0; i < s.size(); ++i) {
        t += s[i];
        t += "#";
    }
    int mx=0;
    // Process t
    vector<int> p(t.size(), 0);
    int mx = 0, id = 0, resLen = 0, resCenter = 0;
    for (int i = 1; i < t.size(); ++i) {
        p[i] = mx > i ? min(p[2 * id - i], mx - i) : 1;
        while (t[i + p[i]] == t[i - p[i]]) ++p[i];
        if (mx < i + p[i]) {
            mx = i + p[i];
            id = i;
        }
        if (resLen < p[i]) {
            resLen = p[i];
            resCenter = i;
        }
        mx=max(mx,p[i]);
    }
    cout<<mx-1<<endl;
    return s.substr((resCenter - resLen) / 2, resLen - 1);
}

字符串哈希

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
typedef unsigned long long ull;
const ull Seed_Pool[] = {146527, 19260817};
const ull Mod_Pool[] = {1000000009, 998244353};
struct Hash
{
    ull SEED, MOD;
    vector<ull> p, h;
    Hash() {}
    Hash(const string& s, const int& seed_index, const int& mod_index)
    {
        SEED = Seed_Pool[seed_index];
        MOD = Mod_Pool[mod_index]; 
        int n = s.length();
        p.resize(n + 1), h.resize(n + 1);
        p[0] = 1;
        for (int i = 1; i <= n; i++) p[i] = p[i - 1] * SEED % MOD;
        for (int i = 1; i <= n; i++) h[i] = (h[i - 1] * SEED % MOD + s[i - 1]) % MOD;
    }
    ull get(int l, int r) { return (h[r] - h[l] * p[r - l] % MOD + MOD) % MOD; }
    ull substr(int l, int m) { return get(l, l + m); }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
    p[0]=1;
    for(int i=1;i<=3e5+10;i++)p[i]=p[i-1]*233;
        for(int i=1;i<=len;i++){
            h[i]=(h[i-1]*233+s[i]);
        }
ull get(int l,int r){
    return h[r]-h[l-1]*p[r-l+1];
}
bool check(int l,int r){
    int len=(r-l+1);
    int mid=(l+r)/2;
    if(len&1)return get(l,mid)==get(mid,r);
    else return get(l,mid)==get(mid+1,r);
}

回文树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
const int MAXN = 100005 ;  
const int N = 26 ;  

struct Palindromic_Tree {  
    //cnt最后count一下之后是那个节点代表的回文串出现的次数
    int next[MAXN][N] ;//next指针，next指针和字典树类似，指向的串为当前串两端加上同一个字符构成  
    int fail[MAXN] ;//fail指针，失配后跳转到fail指针指向的节点  
    int cnt[MAXN] ; //表示节点i表示的本质不同的串的个数（建树时求出的不是完全的，最后count()函数跑一遍以后才是正确的） 
    int num[MAXN] ; //表示以节点i表示的最长回文串的最右端点为回文串结尾的回文串个数
    int len[MAXN] ;//len[i]表示节点i表示的回文串的长度（一个节点表示一个回文串）
    int S[MAXN] ;//存放添加的字符  
    int last ;//指向新添加一个字母后所形成的最长回文串表示的节点。
    int n ;//表示添加的字符个数。
    int p ;//表示添加的节点个数。

    int newnode ( int l ) {//新建节点  
        for ( int i = 0 ; i < N ; ++ i ) next[p][i] = 0 ;  
        cnt[p] = 0 ;  
        num[p] = 0 ;  
        len[p] = l ;  
        return p ++ ;  
    }  

    void init () {//初始化  
        p = 0 ;  
        newnode (  0 ) ;  
        newnode ( -1 ) ;  
        last = 0 ;  
        n = 0 ;  
        S[n] = -1 ;//开头放一个字符集中没有的字符，减少特判  
        fail[0] = 1 ;  
    }  

    int get_fail ( int x ) {//和KMP一样，失配后找一个尽量最长的  
        while ( S[n - len[x] - 1] != S[n] ) x = fail[x] ;  
        return x ;  
    }  

    void add ( int c ) {  
        c -= 'a' ;  
        S[++ n] = c ;  
        int cur = get_fail ( last ) ;//通过上一个回文串找这个回文串的匹配位置  
        if ( !next[cur][c] ) {//如果这个回文串没有出现过，说明出现了一个新的本质不同的回文串  
            int now = newnode ( len[cur] + 2 ) ;//新建节点  
            fail[now] = next[get_fail ( fail[cur] )][c] ;//和AC自动机一样建立fail指针，以便失配后跳转  
            next[cur][c] = now ;  
            num[now] = num[fail[now]] + 1 ;  
        }  
        last = next[cur][c] ;  
        cnt[last] ++ ;  
    }  

    void count () {  
        for ( int i = p - 1 ; i >= 0 ; -- i ) cnt[fail[i]] += cnt[i] ;  
        //父亲累加儿子的cnt，因为如果fail[v]=u，则u一定是v的子回文串！  
    }  
} ;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
struct PAT{
    struct node{
        int len,num,fail,son[26];
    }t[maxn];
    int last,n,tot,s[maxn],x[maxn],y[maxn];ll sum[maxn];
    void init(int len){
        for(int i=0;i<=len+10;i++){
            t[i].fail=t[i].num=t[i].len=0;
            for(int j=0;j<26;j++)t[i].son[j]=0;
            x[i]=y[i]=0;sum[i]=0;
        }
        tot=last=1;n=0;
        t[0].len=0;t[1].len=-1;
        t[0].fail=t[1].fail=1;
        s[0]=-1;
    }
    void add(int c){
        int p=last;s[++n]=c;
        while(s[n]!=s[n-1-t[p].len])p=t[p].fail;
        if(!t[p].son[c]){
            int v=++tot,k=t[p].fail;
            while(s[n]!=s[n-1-t[k].len])k=t[k].fail;
            t[v].fail=t[k].son[c];
            t[v].len=t[p].len+2;
            t[v].num=t[t[v].fail].num+1;///可以通过深度来求所有回文个数
            t[p].son[c]=v;
        }
        last=t[p].son[c];
        sum[last]++;
    }
    void solve(){
        for(int i=tot;i>=2;i--){
            if(x[i]==0)x[i]=i;
            while(x[i]>=2&&t[x[i]].len>(t[i].len+1)/2)x[i]=t[x[i]].fail;
            if(x[i]>=2&&t[x[i]].len==(t[i].len+1)/2)y[i]=1;
            x[t[i].fail]=x[i];
        }

        for(int i=tot;i>=2;i--){
            sum[t[i].fail]+=sum[i]; 
            if(y[i])ans[t[i].len]+=sum[i];
        }
    }
}T;

支持前后端插入回文树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
struct PAT
{
    struct node{
        int len,num,fail,son[26];
    }t[maxn];
    int n,tot,s[maxn<<1],L,R,suf,pre; ll ans;
    void init()
    {
        memset(t,0,sizeof(t));
        memset(s,-1,sizeof(s));
        tot=1; L=100000; R=L-1;
        suf=pre=0; ans=0;
        t[1].len=-1; t[0].fail=t[1].fail=1;
    }
    void add(int c,int n,int &last,int op){
        int p=last; s[n]=c;
        while(s[n]!=s[n-op-op*t[p].len]) p=t[p].fail;
        if(!t[p].son[c]){
            int v=++tot,k=t[p].fail;
            while(s[n]!=s[n-op*t[k].len-op]) k=t[k].fail;
            t[v].fail=t[k].son[c];
            t[v].len=t[p].len+2;
            t[v].num=t[t[v].fail].num+1;
            t[p].son[c]=v;
        }
        last=t[p].son[c]; ans+=t[last].num;
        if(t[last].len==R-L+1) suf=pre=last;
    }
}T;
 T.add(s[0]-'a',--T.L,T.pre,-1);
 T.add(s[0]-'a',++T.R,T.suf,1);

AC自动机

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
struct Trie{
    int next[maxm][26],fail[maxm],end[maxm];
    int root,L;
    int newnode(){
    for(int i=0;i<26;i++)
        next[L][i]=-1;
    end[L++]=0;
    return L-1;
    }
    void init(){
        L=0;
        root=newnode();
    }
    void insert(char buf[]){
        int len=strlen(buf);
        int now=root;
        for(int i=0;i<len;i++){
            if(next[now][buf[i]-'a']==-1)
                next[now][buf[i]-'a']=newnode();
            now=next[now][buf[i]-'a'];
        }
        end[now]++;
    }
    void build(){
        queue<int>Q;
        fail[root]=root;
        for(int i=0;i<26;i++)
            if(next[root][i]==-1)
                next[root][i]=root;
            else{
                fail[next[root][i]]=root;
                Q.push(next[root][i]);
            }
        while(!Q.empty()){
            int now=Q.front();
            Q.pop();
            for(int i=0;i<26;i++)
                if(next[now][i]==-1)
                    next[now][i]=next[fail[now]][i];
                else{
                    fail[next[now][i]]=next[fail[now]][i];
                    Q.push(next[now][i]);
                }
        }
    }
    int query(char buf[]){
        int len=strlen(buf);
        int now=root;
        int res=0;
        for(int i=0;i<len;i++){
            now=next[now][buf[i]-'a'];
            int temp=now;
            while(temp!=root){
                res+=end[temp];
                end[temp]=0;
                temp=fail[temp];
            }
        }
        return res;
    }
    void debug(){
        for(int i=0;i<L;i++){
            printf("id =%3d,fail = %3d,end = %3d ,chi = [",i,fail[i],end[i]);
            for(int j=0;j<26;j++)
                printf("%2d",next[i][j]);
            printf("]\n");
        }
    }
};

后缀数组

倍增法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
struct DA{
//sa[i]就表示排名为i的后缀的起始位置的下标
//映射数组rk[i]就表示起始位置的下标为i的后缀的排名
/*height 数组的定义：h[i]表示rk为i的后缀与rk为i−1的后缀的最长公共前缀，可以用sa数组和rk数组来O(n)求得，这要用到一个性质：h[rk[i]]>=h[rk[i−1]]−1。也就是说如果根据rk从前往后求，每次暴力匹配来增加长度，结果是近似递增的，可以证明时间复杂度的正确性。性质的证明详见论文
*/
    bool cmp(int *r,int a,int b,int l){
        return r[a]==r[b]&&r[a+l]==r[b+l];
    }
    int t1[maxn],t2[maxn],c[maxn];
    int rank[maxn],height[maxn],RMQ[maxn],mm[maxn];
    int best[20][maxn];
    int r[maxn];
    int sa[maxn];
    int str[maxn];
    void da(int n,int m){
        n++;
        int i,j,p,*x=t1,*y=t2;
        for(i=0;i<m;i++)c[i]=0;
        for(i=0;i<n;i++)c[x[i]=str[i]]++;
        for(i=1;i<m;i++)c[i]+=c[i-1];
        for(i=n-1;i>=0;i--)sa[--c[x[i]]]=i;
        for(j=1;j<=n;j<<=1){
            p=0;
            for(i=n-j;i<n;i++)y[p++]=i;
            for(i=0;i<n;i++)if(sa[i]>=j)y[p++]=sa[i]-j;
            for(i=0;i<m;i++)c[i]=0;
            for(i=0;i<n;i++)c[x[y[i]]]++;
            for(i=1;i<m;i++)c[i]+=c[i-1];
            for(i=n-1;i>=0;i--)sa[--c[x[y[i]]]]=y[i];
            swap(x,y);
            p=1;x[sa[0]]=0;
            for(i=1;i<n;i++)
                x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++;
            if(p>=n)break;
            m=p;
        }
        int k=0;
        n--;
        for(i=0;i<=n;i++)rank[sa[i]]=i;
        for(i=0;i<n;i++){
            if(k)k--;
            j=sa[rank[i]-1];
            while(str[i+k]==str[j+k])k++;
            height[rank[i]]=k;
        }
    }
    void initRMQ(int n){
        for(int i=1;i<=n;i++)RMQ[i]=height[i];
        mm[0]=-1;
        for(int i=1;i<=n;i++)
            mm[i]=((i&(i-1))==0)?mm[i-1]+1:mm[i-1];
        for(int i=1;i<=n;i++)best[0][i]=i;
        for(int i=1;i<=mm[n];i++)
        for(int j=1;j+(1<<i)-1<=n;j++){
            int a=best[i-1][j];
            int b=best[i-1][j+(1<<(i-1))];
            if(RMQ[a]<RMQ[b])best[i][j]=a;
            else best[i][j]=b;
        }
    }
    int askRMQ(int a,int b){
        int t;
        t=mm[b-a+1];
        b-=(1<<t)-1;
        a=best[t][a];b=best[t][b];
        return RMQ[a]<RMQ[b]?a:b;
    }
    int lcp(int a,int b){
        a=rank[a];b=rank[b];
        if(a>b)swap(a,b);
        return height[askRMQ(a+1,b)];
    }
    void print(int n){
        cout<<"sa[] ";
        for(int i=0;i<=n;i++)cout<<sa[i]<<" ";cout<<endl;
        cout<<"rank[] ";
        for(int i=0;i<=n;i++)cout<<rank[i]<<" ";cout<<endl;
        cout<<"height[] ";
        for(int i=0;i<=n;i++)cout<<height[i]<<" ";cout<<endl;
    }
}AA,BB;
//n=8;
//* num[] = { 1, 1, 2, 1, 1, 1, 1, 2, $ }; 注意 num 最后一位为 0，其他 大于 0
//*rank[] = 4, 6, 8, 1, 2, 3, 5, 7, 0 ;rank[0 n-1] 为有效值，rank[n] 必定为 0 无效值
// *sa[] =  8, 3, 4, 5, 0, 6, 1, 7, 2 ;sa[1 n] 为有效值，sa[0] 必定为 n 是 无效值 
//*height[]= 0, 0, 3, 2, 3, 1, 2, 0, 1 ;height[2 n] 为有效值

DC3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
struct DA{
    #define F(x) ((x)/3+((x)%3==1?0:tb))
    #define G(x) ((x)<tb?(x)*3+1:((x)-tb)*3+2)
    int sa[maxn*20],rank[maxn*20],height[maxn*20],str[maxn*20];
    int wa[maxn*20],wb[maxn*20],wv[maxn*20],wss[maxn*20];
    int c0(int *r,int a,int b){
        return r[a]==r[b]&&r[a+1]==r[b+1]&&r[a+2]==r[b+2];
    }
    int c12(int k,int *r,int a,int b){
        if(k==2)
            return r[a]<r[b]||(r[a]==r[b]&&c12(1,r,a+1,b+1));
        else return r[a]<r[b]||(r[a]==r[b]&&wv[a+1]<wv[b+1]);
    }
    void sort(int *r,int *a,int *b,int n,int m){
        int i;
        for(i=0;i<n;i++)wv[i]=r[a[i]];
        for(i=0;i<m;i++)wss[i]=0;
        for(i=0;i<n;i++)wss[wv[i]]++;
        for(i=1;i<m;i++)wss[i]+=wss[i-1];
        for(i=n-1;i>=0;i--)
            b[--wss[wv[i]]]=a[i];
    }
    void dc3(int *r,int *sa,int n,int m){
        int i,j,*rn=r+n;
        int *san=sa+n,ta=0,tb=(n+1)/3,tbc=0,p;
        r[n]=r[n+1]=0;
        for(i=0;i<n;i++)if(i%3!=0)wa[tbc++]=i;
        sort(r+2,wa,wb,tbc,m);
        sort(r+1,wb,wa,tbc,m);
        sort(r,wa,wb,tbc,m);
        for(p=1,rn[F(wb[0])]=0,i=1;i<tbc;i++)
            rn[F(wb[i])]=c0(r,wb[i-1],wb[i])?p-1:p++;
        if(p<tbc)dc3(rn,san,tbc,p);
        else for(i=0;i<tbc;i++)san[rn[i]]=i;
        for(i=0;i<tbc;i++)if(san[i]<tb)wb[ta++]=san[i]*3;
        if(n%3==1)wb[ta++]=n-1;
        sort(r,wb,wa,ta,m);
        for(i=0;i<tbc;i++)wv[wb[i]=G(san[i])]=i;
        for(i=0,j=0,p=0;i<ta&&j<tbc;p++)
            sa[p]=c12(wb[j]%3,r,wa[i],wb[j])?wa[i++]:wb[j++];
        for(;i<ta;p++)sa[p]=wa[i++];
        for(;j<tbc;p++)sa[p]=wb[j++];
    }
    void da(int n,int m){
        for(int i=n;i<n*3;i++)str[i]=0;
        dc3(str,sa,n+1,m);
        int i,j,k=0;
        for(i=0;i<=n;i++)rank[sa[i]]=i;
        for(i=0;i<n;i++){
            if(k)k--;
            j=sa[rank[i]-1];
            while(str[i+k]==str[j+k])k++;
            height[rank[i]]=k;
        }
    }
    void print(int n){
        cout<<"sa[] ";
        for(int i=0;i<=n;i++)cout<<sa[i]<<" ";cout<<endl;
        cout<<"rank[] ";
        for(int i=0;i<=n;i++)cout<<rank[i]<<" ";cout<<endl;
        cout<<"height[] ";
        for(int i=0;i<=n;i++)cout<<height[i]<<" ";cout<<endl;
    }
}DA;

后缀自动机

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
struct SAM{
    int fa[maxn],ch[maxn][26],maxlen[maxn],tot,last;
    int sz[maxn],a[maxn],b[maxn];
    void init(){
        tot=last=1;maxlen[1]=fa[1]=0;
        memset(ch[1],0,sizeof(ch[1]));
    }
    void add(int x){
        int np=++tot,p=last;last=np;
        maxlen[np]=maxlen[p]+1;sz[np]=1;
        memset(ch[np],0,sizeof(ch[np]));
        while(p&&!ch[p][x])ch[p][x]=np,p=fa[p];
        if(!p)fa[np]=1;
        else{
            int q=ch[p][x];
            if(maxlen[q]==maxlen[p]+1)fa[np]=q;
            else{
                int nq=++tot;
                memcpy(ch[nq],ch[q],sizeof(ch[q]));
                fa[nq]=fa[q],fa[np]=fa[q]=nq;
                maxlen[nq]=maxlen[p]+1;
                while(p&&ch[p][x]==q)ch[p][x]=nq,p=fa[p];
            }
        }
    }
    void sort(){///拓扑排序 得到每个集合里的串出现次数
        for(int i=1;i<=tot;i++)a[i]=0;
        for(int i=1;i<=tot;i++)a[maxlen[i]]++;
        for(int i=1;i<=tot;i++)a[i]+=a[i-1];
        for(int i=1;i<=tot;i++)b[a[maxlen[i]]--]=i;
        for(int i=tot;i;i--)sz[fa[b[i]]]+=sz[b[i]];
    }
    int At[maxn],Len[maxn];
    void go(char s[]){
        int len=strlen(s);
        int now=1,nowl=0;
        for(int i=0;i<len;i++){
            int c=s[i]-'a';
            if(ch[now][c])now=ch[now][c],nowl++;
            else{
                while(now&&!ch[now][c])now=fa[now];
                if(!now)now=1,nowl=0;
                else nowl=maxlen[now]+1,now=ch[now][c];
            }
            At[i+1]=now;Len[i+1]=nowl;
        }
    }
}S;

树链剖分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
int n,q,a[maxn];
vector<int>G[maxn];
int size[maxn],son[maxn],fa[maxn],dep[maxn],top[maxn];
int id[maxn],pre[maxn],cnt=0;
void dfs1(int u,int f,int deep){
    size[u]=1;
    fa[u]=f;son[u]=0;dep[u]=deep;
    for(int i=0;i<G[u].size();i++){
        int v=G[u][i];
        if(v==f)continue;
        dfs1(v,u,deep+1);
        size[u]+=size[v];
        if(size[v]>size[son[u]])son[u]=v;
    }
}
void dfs2(int u,int root){
    id[u]=++cnt;top[u]=root;pre[cnt]=u;
    if(son[u])dfs2(son[u],root);
    for(int i=0;i<G[u].size();i++){
        int v=G[u][i];
        if(v==fa[u]||v==son[u])continue;
        dfs2(v,v);
    }
}
int sumv[maxn<<2],maxv[maxn<<2];
inline void pushup(int o){
    sumv[o]=sumv[o<<1]+sumv[o<<1|1];
    maxv[o]=max(maxv[o<<1],maxv[o<<1|1]);
}
void build(int o,int l,int r){
    int mid=(l+r)/2;
    if(l==r){
        sumv[o]=maxv[o]=a[pre[l]];return;
    }
    build(o<<1,l,mid);build(o<<1|1,mid+1,r);
    pushup(o);
}
void update(int o,int l,int r,int q,int v){
    int mid=(l+r)/2;
    if(l==r){
        sumv[o]=maxv[o]=v;return;
    }
    if(q<=mid)update(o<<1,l,mid,q,v);
    else update(o<<1|1,mid+1,r,q,v);
    pushup(o);
}
int querysum(int o,int l,int r,int ql,int qr){
    int mid=(l+r)/2,ans=0;
    if(ql<=l&&r<=qr)return sumv[o];
    if(ql<=mid)ans+=querysum(o<<1,l,mid,ql,qr);
    if(qr>mid)ans+=querysum(o<<1|1,mid+1,r,ql,qr);
    return ans;
}
int querymax(int o,int l,int r,int ql,int qr){
    int mid=(l+r)/2,ans=-inf;
    if(ql<=l&&r<=qr)return maxv[o];
    if(ql<=mid)ans=max(ans,querymax(o<<1,l,mid,ql,qr));
    if(qr>mid)ans=max(ans,querymax(o<<1|1,mid+1,r,ql,qr));
    return ans;
}
int qsum(int u,int v){
    int ans=0;
    while(top[u]!=top[v]){
        if(dep[top[u]]<dep[top[v]])swap(u,v);
        ans+=querysum(1,1,n,id[top[u]],id[u]);
        u=fa[top[u]];
    }
    if(dep[u]<dep[v])swap(u,v);
    ans+=querysum(1,1,n,id[v],id[u]);
    return ans;
}
int qmax(int u,int v){
    int ans=-inf;
    while(top[u]!=top[v]){
        if(dep[top[u]]<dep[top[v]])swap(u,v);
        ans=max(ans,querymax(1,1,n,id[top[u]],id[u]));
        u=fa[top[u]];
    }
    if(dep[u]<dep[v])swap(u,v);
    ans=max(ans,querymax(1,1,n,id[v],id[u]));
    return ans;
}

虚树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
考虑得到了询问点，如何构造出一棵虚树。
首先我们要先对整棵树dfs一遍，求出他们的dfs序，然后对每个节点以dfs序为关键字从小到大排序
同时维护一个栈，表示从根到栈顶元素这条链
假设当前要加入的节点为p，栈顶元素为x=s[top]，lca为他们的最近公共祖先
因为我们是按照dfs序遍历，因此lca不可能是p
那么现在会有两种情况

1.lca是x，直接将p入栈。
2.x,p分别位于lca的两棵子树中，此时x这棵子树已经遍历完毕，（如果没有，即x的子树中还有一个未加入的点y，但是dfn[y]<dfn[p]，即应先访问y）， 我们需要对其进行构建

设栈顶元素为x，第二个元素为y
若dfn[y]>dfn[lca]，可以连边y−>x，将x出栈；
若dfn[y]=dfn[lca]，即y=lca，连边lca−>x，此时子树构建完毕(break)；
若dfn[y]<dfn[lca]，即lca在y,x之间，连边lca−>x，x出栈，再将lca入栈。此时子树构建完毕(break)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
vector<int>G[maxn];
int dep[maxn],id[maxn],cnt,cnt2;
int a[maxn],vis[maxn];
int fa[maxn][22];
int op[maxn],u[maxn],v[maxn],k[maxn];

void dfs(int u,int f){
    dep[u]=dep[f]+1;
    fa[u][0]=f;
    id[u]=++cnt;
    if(vis[u])a[++cnt2]=u;
    for(auto v:G[u]){
        if(v==f)continue;
        dfs(v,u);
    }
}
void init(){
    for(int i=1;i<=20;i++){
        for(int j=1;j<=n;j++){
            int v=fa[j][i-1];
            fa[j][i]=fa[v][i-1];
        }
    }
}
int lca(int p,int q){
    if(dep[p]<dep[q])swap(p,q);
    for(int i=20;i>=0;i--){
        if(dep[fa[p][i]]>=dep[q])p=fa[p][i];
    }
    if(p==q)return q;
    for(int i=20;i>=0;i--){
        if(fa[p][i]!=fa[q][i])p=fa[p][i],q=fa[q][i];
    }
    return fa[p][0];
}
int S[maxn],top;
int f[maxn];
int sz[maxn];
ll va[maxn],val[maxn]; 
void add(int u,int v){
    if(dep[u]<dep[v])swap(u,v);
    f[u]=v;
    val[u]=0;
    sz[u]=dep[u]-dep[v]-1,va[u]=0; ///链上的个数 和值。
}

void insert(int x){
    if(top==1){
        S[++top]=x;
        return;
    }
    int lc=lca(x,S[top]);
    if(lc==S[top]){
        S[++top]=x;return;
    }
    while(top>1&&id[S[top-1]]>=id[lc])
        add(S[top-1],S[top]),top--;
    if(lc!=S[top])add(lc,S[top]),S[top]=lc;
    S[++top]=x;
}

void build(){
    S[top=1]=0;
    for(int i=1;i<=cnt2;i++)
        insert(a[i]);
    while(top>1)
        add(S[top-1],S[top]),top--;
}
//main
        for(int i=1;i<n;i++){
            int u,v;cin>>u>>v;
            G[u].push_back(v);
            G[v].push_back(u);
        }
        for(int i=1;i<=m;i++){
            cin>>op[i]>>u[i]>>v[i];
            if(op[i]<=3||op[i]==7)cin>>k[i];
            vis[u[i]]=1;vis[v[i]]=1;
        }
        vis[1]=1;
        dfs(1,0);init();
        build();
        for(int i=1;i<=m;i++){
            get(op[i],u[i],v[i],k[i]);
        }

树分治

点分治

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
int Laxt[maxn<<1],Next[maxn<<1],To[maxn<<1],Len[maxn<<1],ppp;

void add(int u,int v,int w){
    Next[++ppp]=Laxt[u];Laxt[u]=ppp;To[ppp]=v;Len[ppp]=w;
    Next[++ppp]=Laxt[v];Laxt[v]=ppp;To[ppp]=u;Len[ppp]=w;
}
int sz[maxn],d[maxn],vis[maxn],root,sum;
void findroot(int u,int fa){//找重心
    sz[u]=1;d[u]=0;
    for(int i=Laxt[u];i;i=Next[i]){
        int v=To[i];
        if(vis[v]||v==fa)continue;
        findroot(v,u);
        sz[u]+=sz[v];
        d[u]=max(d[u],sz[v]);
    }
    d[u]=max(d[u],sum-sz[u]);
    if(d[u]<d[root])root=u;
}
int dep[maxn],a[maxn];
void dfsdeep(int u,int fa){//计算长度
    a[++a[0]]=dep[u];
    for(int i=Laxt[u];i;i=Next[i]){
        int v=To[i];
        if(vis[v]||v==fa)continue;
        dep[v]=dep[u]+Len[i];
        dfsdeep(v,u);
    }
}
int L;
int cal(int u,int now){//计算答案
    dep[u]=now;a[0]=0;
    dfsdeep(u,0);
    sort(a+1,a+1+a[0]);
    int l=1,r=a[0],ans=0;
    while(l<r){
        if(a[l]+a[r]<=L)ans+=r-l,l++;
        else r--;
    }
    return ans;
}
int ans;
void solve(int u){//解决者
    vis[u]=1;
    ans+=cal(u,0);
    for(int i=Laxt[u];i;i=Next[i]){
        int v=To[i];
        if(vis[v])continue;
        ans-=cal(v,Len[i]);
        sum=sz[v];
        root=0;findroot(v,0);
        solve(root);
    }
}

不需要容斥的点分治

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
int a[N], dis[10000003];
int md[N], MK, cnt;
void getdis(int now, int pre, int di) {
    if (di > MK)return ;
    md[++cnt] = di;
    for (auto k : v[now]) {
        if (vis[k.fi] || k.fi == pre)continue;
        getdis(k.fi, now, di + k.se);
    }
}
int qa[N], tmp;
void get(int now, int pre) {
    dis[0] = 1;
    for (auto k : v[now]) {
        if (k.fi == pre || vis[k.fi])continue;
        cnt = 0;
        getdis(k.fi, now, k.se);
        for (int i = 1; i <= cnt; ++i) {
            for (int j = 1; j <= m; j++) {
                if (q[j] >= md[i])a[j] |= dis[q[j] - md[i]];
            }
        }
        for (int i = 1; i <= cnt; i++)dis[md[i]] = 1, qa[++tmp] = md[i];
    }
}
void dfs(int now) {
    vis[now] = 1;
    tmp = 0;
    get(now, 0);
    for (int i = 1; i <= tmp; i++)dis[qa[i]] = 0;
    for (auto k : v[now]) {
        if (vis[k.fi])continue;
        rt = 0;
        n = sz[k.fi];
        root(k.fi, 0);
        dfs(rt);
    }
    return ;
}
————————————————
版权声明：本文为CSDN博主「pubgoso」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_40655981/article/details/100886381

动态点分治

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
/*
给你一颗有点权边权均为1的树
每次操作要么修改某点点权，
要么查询距离u点不超过d距离的所有点权的和
*/
#include<bits/stdc++.h>
using namespace std;
const int maxn=3e5+50;
typedef long long ll;
const int inf=1e9;
int d[maxn*2][20],dep[maxn],id[maxn],w[maxn],cnt;
vector<int>G[maxn];
#define bug cout<<"bug"<<endl;
struct bit{
    int n;
    vector<int>c;
    #define lowbit(x) ((x&-x))
    void init(int m){
        this->n=m;
        c.clear();
        for(int i=0;i<=n;i++)
            c.push_back(0);
    }
    void up(int x,int v){
        if(!x)c[x]+=v;
        for(;x<=n&&x;x+=lowbit(x))
            c[x]+=v;
    }
    int qu(int x){
        if(x>n)x=n;
        int res=c[0];
        for(;x;x-=lowbit(x))
            res+=c[x];
        return res;
    }
    #undef lowbit
}T[maxn*2];
int n,sum,rt,f[maxn],vis[maxn],luo,sz[maxn];
void init(){
    for(int i=1;i<=n;i++)
        G[i].clear(),vis[i]=f[i]=0;
    cnt=0;
}
void dfs(int u,int fa){
    dep[u]=dep[fa]+1;
    d[++cnt][0] = dep[u];
    id[u] = cnt;
    for(auto v:G[u]){
        if(v==fa)continue;
        dfs(v, u);
        d[++cnt][0]=dep[u];
    }
}
void rmq_init(){
    for(int i=1;i<=18;i++)
        for(int j=1;j+(1<<i)-1<=cnt;j++)
            d[j][i]=min(d[j][i-1],d[j+(1<<i-1)][i-1]);
}
int LCA(int x,int y){
    int l=id[x],r=id[y];
    if(l>r)swap(l,r);
    int k=log2(r-l+1);
    return min(d[l][k],d[r+1-(1<<k)][k]);
}
int dis(int x,int y){
    return dep[x]+dep[y]-2*LCA(x,y);
}
void findrt(int u,int fa){
    sz[u]=1;
    int mx=0;
    for(auto v:G[u]){
        if(v==fa||vis[v])continue;
        findrt(v,u);
        sz[u]+=sz[v];
        mx=max(mx,sz[v]);
    }
    mx=max(mx,sum-sz[u]);
    if(mx<luo)luo=mx,rt=u;
}
void divide(int u,int fa){
    f[u]=fa;
    vis[u]=1;
    T[u].init(sum);
    T[u+n].init(sum);
    int tmp=sum;
    for(auto v:G[u]){
        if(v==fa||vis[v])continue;
        sum=(sz[v]>sz[u])?tmp-sz[u]:sz[v];
        luo=inf;
        findrt(v,0);
        divide(rt,u);
    }
}
void up(int u,int v,int val){
    if(!u)return;
    int dist=dis(u,v);
    T[u].up(dist,val);
    if(f[u]){
        int dist2=dis(f[u],v);
        T[u+n].up(dist2,val);
    }
    up(f[u],v,val);
}
int gao(int u,int v,int d){
    int luo=0,dist=dis(u,v);
    if(dist<=d)
        luo+=T[u].qu(d-dist);
    if(f[u]){
        dist=dis(f[u],v);
        if(dist<=d)
            luo-=T[u+n].qu(d-dist);
        luo+=gao(f[u],v,d);
    }
    return luo;
}
int main(){
    int q,u,v;
    char ch;
    while(cin>>n>>q){
        init();
        for(int i=1;i<=n;i++)cin>>w[i];
        for(int i=1;i<n;i++){
            cin>>u>>v;
            G[u].push_back(v);G[v].push_back(u);
        }
        dfs(1,0);
        rmq_init();
        sum=n;
        luo=inf;
        findrt(1,0);
        divide(rt,0);
        for(int i=1;i<=n;i++)up(i,i,w[i]);
        while(q--){
            cin>>ch>>u>>v;
            if(ch=='?')cout<<gao(u,u,v)<<endl;
            else{
                up(u,u,v-w[u]);
                w[u]=v;
            }
        }
    }
    return 0;
}

可以任意删除元素的优先队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

struct node//手搓一个可以删除任意元素的优先队列。
{
    priority_queue<int>q,del;
    void Push(int x){q.push(x);}
    void Erase(int x){del.push(x);}
    int Top()
    {
        while(del.size()&&del.top()==q.top()) del.pop(),q.pop();
        return q.top();
    }
    void Pop()
    {
        while(del.size()&&del.top()==q.top()) del.pop(),q.pop();
        q.pop();
    }
    int Sectop() ///第二大
    {
        int tmp1=Top();Pop();int tmp2=Top();
        Push(tmp1); return tmp2;
    }
    int Size() {return q.size()-del.size();}
}c[maxn],d[maxn],ans;

可持续化字典树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
int sum[maxn * 35], son[maxn * 35][2],root[maxn];

void insert(int pos,int pre,int &now,int v){

	now = ++num;
	son[now][0] = son[pre][0];
	son[now][1] = son[pre][1];
	sum[now] = sum[pre] + 1;
	if(pos==-1)
		return;
	bool k = v & (1 << pos);
	insert(pos - 1, son[pre][k], son[now][k], v);
}
int query(int pos,int st,int en,int v){
	//cout << "pos=" << pos << " v=" << v << endl;
	if(pos<0)
		return 0;
	int k = !(v & (1 << pos));
	int tmp = sum[son[en][k]] - sum[son[st][k]];

	if(tmp>0)
		return query(pos - 1, son[st][k], son[en][k], v) + (1 << pos);
	else
		return query(pos - 1, son[st][k ^ 1], son[en][k ^ 1], v);
}
int cnt;

int val[maxn],in[maxn],out[maxn],id[maxn];

void dfs(int u){
	in[u]=++cnt;
	id[cnt]=u;
	insert(30, root[in[u] - 1], root[cnt], val[u]);
	for (int i = Laxt[u]; i;i=Next[i]){
		dfs(To[i]);
	}
	out[u] = cnt;
}

线段树合并

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
int ls[maxn*40],rs[maxn*40],rt[maxn*40],num[maxn*40],p;
void push_up(int o){
    if(num[ls[o]]>num[rs[o]])num[o]=num[ls[o]],sum[o]=sum[ls[o]];
    else if(num[rs[o]]>num[ls[o]])num[o]=num[rs[o]],sum[o]=sum[rs[o]];
    else num[o]=num[ls[o]],sum[o]=sum[ls[o]]+sum[rs[o]];
}
void update(int &o,int l,int r,int pos){
    if(!o)o=++p;
    if(l==r){
        sum[o]=l;
        num[o]++;
        return;
    }
    int mid=(l+r)/2;
    if(pos<=mid)update(ls[o],l,mid,pos);
    else update(rs[o],mid+1,r,pos);
    push_up(o);
}

int ins(int o,int pre,int l,int r){
    if(!o)return pre;
    if(!pre)return o;
    if(l==r){
        num[o]+=num[pre];
        sum[o]=l;
        return o;
    }
    int mid=(l+r)/2;
    ls[o]=ins(ls[o],ls[pre],l,mid);
    rs[o]=ins(rs[o],rs[pre],mid+1,r);
    push_up(o);
    return o;
}

void dfs(int u,int pre){
    for(int i=Laxt[u];i;i=Next[i]){
        int v=To[i];if(v==pre)continue;
        dfs(v,u);
        rt[u]=ins(rt[u],rt[v],1,1e5);
    }
    update(rt[u],1,1e5,a[u]);
    ans[u]=sum[rt[u]];
}

主席树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int sum[maxn*40],rt[maxn*40];
int lss[maxn*40],rss[maxn*40];
int cnt;
void update(int &o,int pre,int l,int r,int val){
    o=++cnt;
    lss[o]=lss[pre];rss[o]=rss[pre];
    sum[o]=sum[pre];
    if(l==r){sum[o]++;return;}
    int mid=(l+r)/2;
    if(val<=mid)update(lss[o],lss[pre],l,mid,val);
    else update(rss[o],rss[pre],mid+1,r,val);
}
int query(int o,int l,int r,int val){
    if(l==r){
        return sum[o];
    }
    int mid=(l+r)/2;
    if(val<=mid)return query(lss[o],l,mid,val);
    else return query(rss[o],mid+1,r,val);
}
 update(rt[i],rt[i-1],1,1e9,a[i]);
query(rt[r],1,1e9,gc)
    //查询区间这个数的个数

权值线段树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
ll sum[maxn*40],val[maxn*40];
int ls[maxn*40],rs[maxn*40];
int cnt;
void update(int &o,int l,int r,int k,int num){
    if(!o)o=++cnt;
    sum[o]+=k;
    val[o]+=1LL*k*num;
    val[o]%=mod;
    if(l==r)return;
    int mid=(l+r)/2;
    if(num<=mid)update(ls[o],l,mid,k,num);
    else update(rs[o],mid+1,r,k,num);
}
ll query(int o,int l,int r,ll k){
    if(l==r)return 1LL*k*l%mod;
    int mid=(l+r)/2;
    ll res=0;
    if(k>sum[ls[o]])res=(val[ls[o]]+query(rs[o],mid+1,r,k-sum[ls[o]]));
    else res=query(ls[o],l,mid,k);
    return res%mod;
}

主席树套树状数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
///动态第K大
int sum[maxn*40],ls[maxn*40],rs[maxn*40],rt[maxn*40];
int op[maxn],ql[maxn],qr[maxn];int cnt;int a[maxn];
int lowbit(int x){return x&(-x);}
void update(int &o,int l,int r,int k,int value){
    if(!o)o=++cnt;sum[o]+=value;
    if(l==r)return;int mid=(l+r)/2;
    if(k<=mid)update(ls[o],l,mid,k,value);
    else update(rs[o],mid+1,r,k,value);
}
int c1,c2;
int q1[maxn],q2[maxn];
int query(int l,int r,int k){
    if(l==r)return l;
    int mid=(l+r)/2;int res=0;
    for(int i=1;i<=c2;i++)res+=sum[ls[q2[i]]];
    for(int i=1;i<=c1;i++)res-=sum[ls[q1[i]]];
    if(k<=res){
        for(int i=1;i<=c2;i++)q2[i]=ls[q2[i]];
        for(int i=1;i<=c1;i++)q1[i]=ls[q1[i]];
        return query(l,mid,k);
    }
    else{
        for(int i=1;i<=c2;i++)q2[i]=rs[q2[i]];
        for(int i=1;i<=c1;i++)q1[i]=rs[q1[i]];
        return query(mid+1,r,k-res);
    }
}
int main(){
    std::ios::sync_with_stdio(false);
    int n,m; cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>a[i];
        for(int j=i;j<=n;j+=lowbit(j))update(rt[j],0,1e9,a[i],1);
    }
    while(m--){
        char ch;
        cin>>ch;
        if(ch=='C'){
            int i,t;cin>>i>>t;
            for(int j=i;j<=n;j+=lowbit(j))update(rt[j],0,1e9,a[i],-1);
            a[i]=t;
            for(int j=i;j<=n;j+=lowbit(j))update(rt[j],0,1e9,a[i],1);
        }
        else{
            int l,r,k;
            cin>>l>>r>>k;c1=c2=0;
            for(int i=l-1;i;i-=lowbit(i))q1[++c1]=rt[i];
            for(int i=r;i;i-=lowbit(i))q2[++c2]=rt[i];
            cout<<query(0,1e9,k)<<endl;
        }
    }
    return 0;
}

树状数组套主席树 （二维数点）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
int n,m;
int sum[maxn*170],ls[maxn*170],rs[maxn*170],rt[maxn];
int cnt;
int lowbit(int x){return x&(-x);}
int sta[maxn],top;
int newnode(){ ///回收空间
    int p=top?sta[--top]:++cnt;
    ls[p]=rs[p]=sum[p]=0;
    return p;
}
void update(int &o,int l,int r,int k,int v){
    if(!o)o=newnode();
    sum[o]+=v;
    if(l==r)return ;int mid=(l+r)/2;
    if(k<=mid)update(ls[o],l,mid,k,v);
    else update(rs[o],mid+1,r,k,v);
    if(!sum[o])sta[top++]=o,o=0;
}
int query(int o,int l,int r,int ql,int qr){
    if(ql<=l&&qr>=r)return sum[o];
    int mid=(l+r)/2;
    int ans=0;
    if(ql<=mid)ans+=query(ls[o],l,mid,ql,qr);
    if(qr>mid)ans+=query(rs[o],mid+1,r,ql,qr);
    return ans;
}
int pa[maxn],pb[maxn],a[maxn],b[maxn];
int main(){
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);std::cout.tie(0);
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>a[i],pa[a[i]]=i;
    for(int i=1;i<=n;i++)cin>>b[i],pb[b[i]]=i;
    for(int i=1;i<=n;i++){
        for(int j=pa[i];j<=n;j+=lowbit(j))
            update(rt[j],1,n,pb[i],1);
    }
    while(m--){
        int op;cin>>op;
        if(op==1){
            int la,ra,lb,rb;cin>>la>>ra>>lb>>rb;
            int ans=0;
            for(int i=ra;i;i-=lowbit(i)){
                ans+=query(rt[i],1,n,lb,rb);
            }
            for(int i=la-1;i;i-=lowbit(i)){
                ans-=query(rt[i],1,n,lb,rb);
            }
            cout<<ans<<endl;
        }
        else{
            int x,y;
            cin>>x>>y;
            int aa=b[x];
            int bb=b[y];
            for(int i=pa[aa];i<=n;i+=lowbit(i)){
                update(rt[i],1,n,pb[aa],-1);
            }
            for(int i=pa[bb];i<=n;i+=lowbit(i)){
                update(rt[i],1,n,pb[bb],-1);
            }
            swap(b[x],b[y]);pb[b[x]]=x;pb[b[y]]=y;
            for(int i=pa[aa];i<=n;i+=lowbit(i)){
                update(rt[i],1,n,pb[aa],1);
            }
            for(int i=pa[bb];i<=n;i+=lowbit(i)){
                update(rt[i],1,n,pb[bb],1);
            }
        }
    }
    return 0;
}

可持久化并查集

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#include<bits/stdc++.h>
using namespace std;
const int maxn=2e5+50;
int n,m;
int fa[maxn*40],cnt;
int rt[maxn*40],ls[maxn*40],rs[maxn*40];
int dep[maxn*40];
void build(int &o,int l,int r){
    o=++cnt;
    if(l==r){fa[o]=l;return;}
    int mid=(l+r)/2;
    build(ls[o],l,mid);build(rs[o],mid+1,r);
}
void merge(int &o,int pre,int l,int r,int pos,int Fa){
    o=++cnt;ls[o]=ls[pre];rs[o]=rs[pre];
    if(l==r){
        fa[o]=Fa;
        dep[o]=dep[pre];
        return;
    }
    int mid=(l+r)/2;
    if(pos<=mid)merge(ls[o],ls[pre],l,mid,pos,Fa);
    else merge(rs[o],rs[pre],mid+1,r,pos,Fa);
}
void update(int o,int l,int r,int pos){
    if(l==r){dep[o]++;return;}
    int mid=(l+r)/2;
    if(pos<=mid)update(ls[o],l,mid,pos);
    else update(rs[o],mid+1,r,pos);
}
int query(int o,int l,int r,int pos){
    if(l==r)return o;
    int mid=(l+r)/2;
    if(pos<=mid)return query(ls[o],l,mid,pos);
    else return query(rs[o],mid+1,r,pos);
}
int find(int o,int pos){
    int now=query(o,1,n,pos);
    if(fa[now]==pos)return now;
    else return find(o,fa[now]);
}
int main(){
    cin>>n>>m;
    build(rt[0],1,n);
    int ans=0;
    for(int i=1;i<=m;i++){
        int op,x,y;
        cin>>op>>x;
        if(op==1){
            cin>>y;
            rt[i]=rt[i-1];
            int posx=find(rt[i],x),posy=find(rt[i],y);
            if(posx!=posy){
                if(dep[posx]>dep[posy])swap(posx,posy);
                merge(rt[i],rt[i-1],1,n,fa[posx],fa[posy]);
                if(dep[posx]==dep[posy])update(rt[i],1,n,fa[posy]);
            }
        }
        else if(op==2)rt[i]=rt[x];
        else{
            cin>>y;
            rt[i]=rt[i-1];
            int posx=find(rt[i],x),posy=find(rt[i],y);
            if(fa[posx]==fa[posy])cout<<1<<endl;
            else cout<<0<<endl;
        }
    }
    return 0;
}

笛卡尔树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
        int n,rt;
        cin>>n;
        for(int i=1;i<=n;i++){
            cin>>a[i];
            l[i]=r[i]=0;
            while(!s.empty()&&a[i]>a[s.top()])
                l[i]=s.top(),s.pop();
            if(!s.empty())
                r[s.top()]=i;
            s.push(i);
        }
        while(!s.empty())
            rt=s.top(),s.pop();

void dfs(int u){
    sz[u]=1;
    if(l[u])
        dfs(l[u]),sz[u]+=sz[l[u]];
    if(r[u])
        dfs(r[u]),sz[u]+=sz[r[u]];
    ans=ans*inv[sz[u]]%mod;

二维树状数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
struct BIT2D{
    int n,b[550][550];
    void init(int _n){n=_n;memset(b,0,sizeof(b));}
    void add(int x,int y,int v){
        for(int i=x;i<=n;i+=i&-i)
            for(int j=y;j<=n;j+=j&-j)
                b[i][j]+=v;
    }
    int sum(int x,int y){
        int res=0;
        for(int i=x;i;i-=i&-i)
            for(int j=y;j;j-=j&-j)
                res+=b[i][j];
        return res;
    }
    int sum(int x1,int y1,int x2,int y2){
        return sum(x2,y2)-sum(x1-1,y2)
            -sum(x2,y1-1)+sum(x1-1,y1-1);
    }
}bit;
///区间修改 单点查询
void range_add(int xa, int ya, int xb, int yb, int z){
    add(xa, ya, z);
    add(xa, yb + 1, -z);
    add(xb + 1, ya, -z);
    add(xb + 1, yb + 1, z);
}
///区间修改 区间查询
ll t1[N][N], t2[N][N], t3[N][N], t4[N][N];
void add(ll x, ll y, ll z){
    for(int X = x; X <= n; X += X & -X)
        for(int Y = y; Y <= m; Y += Y & -Y){
            t1[X][Y] += z;
            t2[X][Y] += z * x;
            t3[X][Y] += z * y;
            t4[X][Y] += z * x * y;
        }
}
void range_add(ll xa, ll ya, ll xb, ll yb, ll z){ //(xa, ya) 到 (xb, yb) 的矩形
    add(xa, ya, z);
    add(xa, yb + 1, -z);
    add(xb + 1, ya, -z);
    add(xb + 1, yb + 1, z);
}
ll ask(ll x, ll y){
    ll res = 0;
    for(int i = x; i; i -= i & -i)
        for(int j = y; j; j -= j & -j)
            res += (x + 1) * (y + 1) * t1[i][j]
                - (y + 1) * t2[i][j]
                - (x + 1) * t3[i][j]
                + t4[i][j];
    return res;
}
ll range_ask(ll xa, ll ya, ll xb, ll yb){
    return ask(xb, yb) - ask(xb, ya - 1) - ask(xa - 1, yb) + ask(xa - 1, ya - 1);
}

///一维
/// 单点修改 区间查询
void add(int p, int x){ //这个函数用来在树状数组中直接修改
    while(p <= n) sum[p] += x, p += p & -p;
}
void range_add(int l, int r, int x){ //给区间[l, r]加上x
    add(l, x), add(r + 1, -x);
}
int ask(int p){ //单点查询
    int res = 0; while(p) res += sum[p], p -= p & -p; return res;
}
///区间修改 区间查询
void add(ll p, ll x){
    for(int i = p; i <= n; i += i & -i)
        sum1[i] += x, sum2[i] += x * p;
}
void range_add(ll l, ll r, ll x){
    add(l, x), add(r + 1, -x);
}
ll ask(ll p){
    ll res = 0;
    for(int i = p; i; i -= i & -i)
        res += (p + 1) * sum1[i] - sum2[i];
    return res;
}
ll range_ask(ll l, ll r){
    return ask(r) - ask(l - 1);
}

图论

前向星

1
2
3
4
5
int Next[maxn<<1],To[maxn<<1],Laxt[maxn<<1];
int cnt;
void add(int u,int v){
    Next[++cnt]=Laxt[u];Laxt[u]=cnt;To[cnt]=v;
}

深度优先遍历相关

无向图的双连通分量/点双

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
struct Edge{
    int u,v;
};
///割顶 bccno 无意义
int pre[maxn],iscut[maxn],bccno[maxn],dfs_clock,bcc_cut;
vector<int>G[maxn],bcc[maxn];
stack<Edge>S;
void init(int n){
    for (int i = 0; i < n; i++) G[i].clear();
}
inline void add_edge(int u, int v) { G[u].push_back(v), G[v].push_back(u); }
int dfs(int u,int fa){
    int lowu = pre[u] = ++dfs_clock;
    int child = 0;
    for(int i = 0; i < G[u].size(); i++){
        int v =G[u][i];
        Edge e = (Edge){u,v};
        if(!pre[v]){ ///没有访问过
            S.push(e);
            child++;
            int lowv = dfs(v, u);
            lowu=min(lowu, lowv);                ///用后代更新
            if(lowv >= pre[u]){
                iscut[u]=true;
                bcc_cut++;bcc[bcc_cut].clear();   ///注意 bcc从1开始
                for(;;){
                    Edge x=S.top();S.pop();
                    if(bccno[x.u] != bcc_cut){bcc[bcc_cut].push_back(x.u);bccno[x.u]=bcc_cut;}
                    if(bccno[x.v] != bcc_cut){bcc[bcc_cut].push_back(x.v);bccno[x.v]=bcc_cut;}
                    if(x.u==u&&x.v==v)break;
                }
            }
        }
        else if(pre[v] < pre[u] && v !=fa){
            S.push(e);
            lowu = min(lowu,pre[v]);
        }
    }
    if(fa < 0 && child == 1) iscut[u] = 0;
    return lowu;
}
void find_bcc(int n){
    memset(pre, 0, sizeof(pre));
    memset(iscut, 0, sizeof(iscut));
    memset(bccno, 0, sizeof(bccno));
    dfs_clock = bcc_cut = 0;
    for(int i = 0; i < n;i++)
        if(!pre[i])dfs(i,-1);
}

求无向图的桥和割点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include<iostream>
using namespace std;
#include<cstdio>
#include<cstring>
#include<vector>
#define N 201
vector<int>G[N];
int n,m,low[N],dfn[N];
bool is_cut[N];
int father[N];
int tim=0;
void input()
{
    scanf("%d%d",&n,&m);
    int a,b;
    for(int i=1;i<=m;++i)
    {
        scanf("%d%d",&a,&b);
        G[a].push_back(b);/*邻接表储存无向边*/
        G[b].push_back(a);
    }
}
void Tarjan(int i,int Father)
{
    father[i]=Father;/*记录每一个点的父亲*/
    dfn[i]=low[i]=tim++;
    for(int j=0;j<G[i].size();++j)
    {
        int k=G[i][j];
        if(dfn[k]==-1)
        {
            Tarjan(k,i);
            low[i]=min(low[i],low[k]);
        }
        else if(Father!=k)/*假如k是i的父亲的话，那么这就是无向边中的重边，有重边那么一定不是桥*/
            low[i]=min(low[i],dfn[k]);//dfn[k]可能！=low[k]，所以不能用low[k]代替dfn[k],否则会上翻过头了。
    }
}
void count()
{
    int rootson=0;
    Tarjan(1,0);
    for(int i=2;i<=n;++i)
    {
        int v=father[i];
        if(v==1)
        rootson++;/*统计根节点子树的个数，根节点的子树个数>=2,就是割点*/
        else{
            if(low[i]>=dfn[v])/*割点的条件*/
            is_cut[v]=true;
        }
    }
    if(rootson>1)
    is_cut[1]=true;
    for(int i=1;i<=n;++i)
    if(is_cut[i])
    printf("%d\n",i);
    for(int i=1;i<=n;++i)
    {
        int v=father[i];
        if(v>0&&low[i]>dfn[v])/*桥的条件*/
        printf("%d,%d\n",v,i);
    }
    
}
int main()
{
    input();
    memset(dfn,-1,sizeof(dfn));
    memset(father,0,sizeof(father));
    memset(low,-1,sizeof(low));
    memset(is_cut,false,sizeof(is_cut));
    count();
    return 0;
}

无向图的强连通分量/边双

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
int Laxt[maxn<<1],Next[maxn<<1],To[maxn<<1],cnt;
void add(int u,int v){
    Next[++cnt]=Laxt[u];
    Laxt[u]=cnt;To[cnt]=v;
}
int low[maxn],dfn[maxn],times,q[maxn],head,scc_cnt,scc[maxn];

void tarjan(int u,int f){
    dfn[u]=low[u]=++times;
    q[++head]=u;
    for(int i=Laxt[u];i;i=Next[i]){
        if(To[i]==f)continue;
        if(!dfn[To[i]]){
            tarjan(To[i],u);
            low[u]=min(low[u],low[To[i]]);
        }
        else low[u]=min(low[u],dfn[To[i]]);
    }
    if(low[u]==dfn[u]){
        scc_cnt++;
        while(true){
            int x=q[head--];
            scc[x]=scc_cnt;
            if(x==u)break;
        }
    }
}

有向图的强连通分量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
vector<int>G[maxn];
int pre[maxn],lowlink[maxn],sccno[maxn],dfs_clock,scc_cnt;
stack<int>S;
inline void init(int n){
    for (int i = 0; i < n; i++) G[i].clear();
}
inline void add_edge(int u, int v) { G[u].push_back(v); }
void dfs(int u){
    pre[u]=lowlink[u]=++dfs_clock;
    S.push(u);
    for(int i=0;i<G[u].size();i++){
        int v=G[u][i];
        if(!pre[v]){
            dfs(v);
            lowlink[u]=min(lowlink[u],lowlink[v]);
        }
        else if(!sccno[v]){
            lowlink[u]=min(lowlink[u],pre[v]);
        }
    }
    if(lowlink[u]==pre[u]){
        scc_cnt++;
        for(;;){
            int x=S.top();S.pop();
            sccno[x]=scc_cnt;
            if(x==u)break;
        }
    }
}
void find_scc(int n){
    dfs_clock=scc_cnt=0;
    memset(sccno,0,sizeof(sccno));
    memset(pre,0,sizeof(pre));
    for(int i=0;i<n;i++)
        if(!pre[i])dfs(i);
}

2-SAT匹配

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
struct TwoSAT{
    int n;
    vector<int> G[maxn*2];
    bool mark[maxn*2];
    int S[maxn*2],c;

    bool dfs(int x){
        if(mark[x^1])return false;
        if(mark[x])return true;
        mark[x]=true;
        S[c++]=x;
        for(int i=0;i<G[x].size();i++)
            if(!dfs(G[x][i]))return false;
        return true;
    }

    void init(int n){
        this->n=n;
        for(int i=0;i<n*2;i++)G[i].clear();
        memset(mark,0,sizeof(mark));
    }
    /// x=xval or y= yval;
    void add_caluse(int x,int xval,int y,int yval){
        x=x*2+xval;
        y=y*2+yval;
        G[x^1].push_back(y);///如果x为真 那么y必须为假;
        G[y^1].push_back(x);///如果y为真 那么x必须为假;
    }

    bool solve(){
        for(int i=0;i<n*2;i+=2)
        if(!mark[i]&&!mark[i+1]){
            c=0;
            if(!dfs(i)){
                while(c>0)mark[S[--c]]=false;
                if(!dfs(i+1))return false;
            }
        }
        return true;
    }
};

最短路

Dijkstra +单源最短路+记录路径O(mlogn)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
struct Edge{
    int from,to,dist;
};
struct HeapNode{
    int d,u;
    bool operator <(const HeapNode& rhs)const{
        return d>rhs.d;
    }
};
struct Dijkstra{
    int n,m;              ///点数和边数  点编号0~N-1
    vector<Edge>edges;    ///边列表
    vector<int>G[maxn];   ///每个节点出发的边编号
    bool done[maxn];      /// 是否已永久标号
    int d[maxn];          /// s到各个点的距离
    int p[maxn];          /// 最短路中的上一条边

    void init(int n){
        this->n=n;
        for(int i=0;i<n;i++)G[i].clear();
        edges.clear();
    }
    void AddEdge(int from,int to,int dist){ ///无向图调用两次
        edges.push_back((Edge){from,to,dist});
        m=edges.size();
        G[from].push_back(m-1);
    }
    void dijkstra(int s){
        priority_queue<HeapNode>Q;
        for(int i=0;i<n;i++)d[i]=inf;
        d[s]=0;
        memset(done,0,sizeof(done));
        Q.push((HeapNode){0,s});
        while(!Q.empty()){
            HeapNode x=Q.top();Q.pop();
            int u=x.u;
            if(done[u])continue;
            done[u]=true;
            for(int i=0;i<G[u].size();i++){
                Edge& e=edges[G[u][i]];
                if(d[e.to]>d[u]+e.dist){
                    d[e.to]=d[u]+e.dist;
                    p[e.to]=G[u][i];
                    Q.push((HeapNode){d[e.to],e.to});
                }
            }
        }
    }
    /// dist[i]为s到i的距离，paths[i]为s到i的最短路径（经过的结点列表，包括s和t）
    void GetShortestPaths(int s,int* dist,vector<int>* paths){///paths是二维链表
        dijkstra(s);
        for(int i=0;i<n;i++){
            dist[i]=d[i];
            paths[i].clear();
            int t=i;
            paths[i].push_back(t);
            while(t!=s){
                paths[i].push_back(edges[p[t]].from);
                t=edges[p[t]].from;
            }
            reverse(paths[i].begin(),paths[i].end());
        }
    }
};

BellmanFord （单源最短路判负环）O(nm)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
struct Edge
{
    int from, to;
    int dist;
    Edge() {}
    Edge(int u, int v, int d) : from(u), to(v), dist(d) {}
};
struct BellmanFord{
    int n,m;
    vector<Edge>edges;
    vector<int> G[maxn];
    bool inq[maxn]; /// 是否在队列中
    int d[maxn];    /// s到各个点的距离  double 要改成double类型
    int p[maxn];    /// 最短路中的上一条弧
    int cnt[maxn];  /// 进队次数
    void init(int n){
        this->n=n;
        for(int i=0;i<n;i++)G[i].clear();
        edges.clear();
    }
    void AddEdge(int from, int to, int dist)
    {
        edges.emplace_back(from, to, dist);
        m = edges.size();
        G[from].push_back(m - 1);
    }
    bool bellmanford(int s){
        queue<int>Q;
        memset(inq,0,sizeof(inq));
        memset(cnt,0,sizeof(cnt));
        for(int i = 0; i < n; i++) { d[i] = 0; inq[0] = true; Q.push(i); } ///如果只判负环用这个
        //for(int i=0;i<n;i++)d[i]=inf;
        //d[s]=0;inq[s]=true;Q.push(s);
        while(!Q.empty()){
            int u=Q.front();
            Q.pop();
            inq[u]=false;
            for(auto& id:G[u]){
                Edge& e=edges[id];
                if(d[u]<inf && d[e.to]>d[u]+e.dist){
                    d[e.to]=d[u] + e.dist;
                    p[e.to]=id;
                    if(!inq[e.to]){
                        Q.push(e.to);
                        inq[e.to]=true;
                        if(++cnt[e.to]>n)return true;
                    }
                }
            }
        }
        return false;
    }
};

Floyd 多源最短路 O(n^3)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
typedef struct{
    char vertex[maxn];        //顶点表
    int edges[maxn][maxn];    //邻接矩阵,可看做边表
    int n,e;                  //图中当前的顶点数和边数
}MGraph;

void Floyd(MGraph g){
    int A[maxn][maxn];
    int path[maxn][maxn];
    int i,j,k,n=g.n;
    for(i=0;i<n;i++)
    for(j=0;j<n;j++){
        A[i][j]=g.edges[i][j];
        path[i][j]=-1;
    }
    for(k=0;k<n;k++)
    for(i=0;i<n;i++)
    for(j=0;j<n;j++)
    if(A[i][j]>(A[i][k]+A[k][j])){
        A[i][j]=A[i][k]+A[k][j];
        path[i][j]=k;
    }
}

FLoyd 判最小环

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
    ///算法思想：如果存在最小环，会在编号最大的点u更新最短路径前找到这个环，发现的方法是，更新最短路径前，遍历i,j点对，一定会发现某对i到j的最短路径长度dis[i][j]+mp[j][u]+mp[u][i] != INF,这时i,j是图中挨着u的两个点，因为在之前最短路更新过程中，u没有参与更新，所以dis[i][j]所表示的路径中不会出现u，如果成立，则一定是一个环。用Floyd算法来实现。但是对于负环此算法失效，因为有负环时，dis[i][j]已经不能保证i到j的路径上不会经过同一个点多次了。
for(int k=1;k<=n;k++){
        for(int i=1;i<k;i++){
            for(int j=i+1;j<k;j++){
                mi=min(dis[i][j]+mp[j][k]+mp[k][i],mi);
            }
        }
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                if(dis[i][j]>(dis[i][k]+dis[k][j])){
                    dis[i][j]=dis[i][k]+dis[k][j];
                }
            }
        }
    }

Floyd 判环(龟兔赛跑算法)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
（1）求环

初始状态下，假设已知某个起点节点为节点S。现设两个指针t和h，将它们均指向S。

同时让t和h往前推进，h的速度为t的2倍），直到h无法前进，即到达某个没有后继的节点时，就可以确定从S出发不会遇到环。反之当t与h再次相遇时，就可以确定从S出发一定会进入某个环，设其为环C。（h和t推进的步数差是环长的倍数）

（2）求环的长度

上述算法刚判断出存在环C时，t和h位于同一节点，设其为节点M。仅需令h不动，而t不断推进，最终又会返回节点M，统计这一次t推进的步数，就是环C的长度。

（3）求环的起点

为了求出环C的起点，只要令h仍均位于节点M，而令t返回起点节点S。随后，同时让t和h往前推进，且速度相同。持续该过程直至t与h再一次相遇，此相遇点就是环C的一个起点。

why？

假设出发起点到环起点的距离为m，已经确定有环，环的周长为n，（第一次）相遇点距离环的起点的距离是k。那么当两者相遇时，慢指针（t）移动的总距离i = m + a * n + k，快指针（h）的移动距离为2i，2i = m + b * n + k。其中，a和b分别为t和h在第一次相遇时转过的圈数。让两者相减（快减慢），那么有i = (b - a) * n。即i是圈长度的倍数。

将一个指针移到出发起点S，另一个指针仍呆在相遇节点M处两者同时移动，每次移动一步。当第一个指针前进了m，即到达环起点时，另一个指针距离链表起点为i + m。考虑到i为圈长度的倍数，可以理解为指针从链表起点出发，走到环起点，然后绕环转了几圈，所以第二个指针也必然在环的起点。即两者相遇点就是环的起点。

最小生成树

有向最小生成树（朱刘算法)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
/// 固定根的最小树型图，邻接矩阵写法
struct MDST{
    int n;
    int w[maxn][maxn];    ///边权
    int vis[maxn];        ///访问标记，仅用来判断无解
    int ans;              ///计算答案
    int removed[maxn];    ///每个点是否被删除
    int cid[maxn];        ///所在圈编号
    int pre[maxn];        ///最小入边的起点
    int iw[maxn];         ///最小入边的权值
    int max_cid;          ///最大圈编号

    void init(int n){
        this->n=n;
        for(int i=0;i<n;i++)
            for(int j=0;j<n;j++)w[i][j]=inf;
    }
    void AddEdge(int u,int v,int cost){
        w[u][v]=min(w[u][v],cost);  ///重边取权值最小的
    }

    ///从s出发能到达多少个结点
    int dfs(int s){
        int ans=1;
        vis[s]=1;
        for(int i=0;i<n;i++)if(!vis[i]&&w[s][i]<inf)ans+=dfs(i);
        return ans;
    }
    ///从u出发沿着pre指针找圈
    bool cycle(int u){
        max_cid++;
        int v=u;
        while(cid[v]!=max_cid){cid[v]=max_cid;v=pre[v];}
        return v==u;
    }
    /// 计算u的最小入弧，入弧起点不得在圈c中
    void update(int u){
        iw[u]=inf;
        for(int i=0;i<n;i++)
        if(!removed[i]&&w[i][u]<iw[u]){
            iw[u]=w[i][u];
            pre[u]=i;
        }
    }
    ///根节点为s,如果失败返回false
    bool solve(int s){
        memset(vis,0,sizeof(vis));
        if(dfs(s)!=n)return false;
        memset(removed,0,sizeof(removed));
        memset(cid,0,sizeof(cid));
        for(int u=0;u<n;u++)update(u);
        pre[s]=s;iw[s]=0;      /// 根结点特殊处理
        ans=max_cid=0;
        for(;;){
            bool have_cycle=false;
            for(int u=0;u<n;u++)if(u!=s&&!removed[u]&&cycle(u)){
                have_cycle=true;
                /// 以下代码缩圈，圈上除了u之外的结点均删除
                int v=u;
                do{
                    if(v!=u)removed[v]=1;
                    ans+=iw[v];
                    /// 对于圈外点i，把边i->v改成i->u（并调整权值）；v->i改为u->i
                    /// 注意圈上可能还有一个v'使得i->v'或者v'->i存在，因此只保留权值最小的i->u和u->i
                    for(int i=0;i<n;i++)if(cid[i]!=cid[u]&&!removed[i]){
                        if(w[i][v]<inf)w[i][u]=min(w[i][u],w[i][v]-iw[v]);
                        w[u][i]=min(w[u][i],w[v][i]);
                        if(pre[i]==v)pre[i]=u;
                    }
                    v=pre[v];
                }while(v!=u);
                update(u);
                break;
            }
            if(!have_cycle)break;
        }
        for(int i=0;i<n;i++)
            if(!removed[i])ans+=iw[i];
        return true;
    }
};

二分图

理论

1
2
3
4
5
6
1.一个二分图中的最大匹配数等于这个图中的最小点覆盖数
2.最小路径覆盖 =|G|-最大匹配数
2.2 可重复先floyd再匹配
3.二分图最大独立集 = 顶点数-二分图最大匹配
  独立集: 图中任意两个顶点都不相连的顶点集合。
4.二分图的最大团=补图的最大独立集

二分图判断

1
2
3
4
5
6
7
8
9
10
11
12
color[maxn];
bool bipartite(int u){
    for(int i = 0;i < G[u].size(); i++){
        int v =G[u][i];
        if(color[v] == color[u])return false;
        if(!color[v]){
            color[v] = 3 - color[u];
            if(!bipartite(v,b))return false;
        }
    }
    return true;
}

匈牙利算法(dfs+bfs)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
bool dfs(int u){
    for(int i=1;i<=n;i++){
        if(G[u][i]&&!vis[i]){
            vis[i]=true;
            if(!P[i]||dfs(P[i])){
                P[i]=u;return true;
            }
        }
    }
    return false;
}
        int ans=0;
        for(int i=1;i<=n;i++){
            memset(vis,false,sizeof(vis));
            if(dfs(i))ans++;
        }
/**************************/
int G[550][550];
bool vis[550];
int lefts[550],rights[550],pre[550];
int mark_rights[550];
int n;
int bfs(){
    memset(lefts,-1,sizeof(lefts));
    memset(rights,-1,sizeof(rights));
    int ans=0;
    for(int i=1;i<=n;i++){
        queue<int>q;
        q.push(i);
        bool flag=false;
        memset(mark_rights,0,sizeof(mark_rights));
        memset(pre,0,sizeof(pre));
        while(!q.empty()){
            int u=q.front();q.pop();
            for(int v=1;v<=n;v++){
                if(G[u][v]&&!mark_rights[v]){
                    mark_rights[v]=1;
                    if(rights[v]==-1){
                        flag=1;
                        int sl=u,sr=v;
                        while(sl!=0){
                            int st=lefts[sl];
                            lefts[sl]=sr;rights[sr]=sl;
                            sl=pre[sl];sr=st;
                        }
                        break;
                    }
                    else{
                        pre[rights[v]]=u;
                        q.push(rights[v]);
                    }
                }
            }
            if(flag)break;
        }
        if(flag)ans++;
    }
    return ans;
}

HK算法(优化匈牙利(√N*M))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
const int maxn=3300+50;
const int inf=1e9;      //距离初始值
int bmap[maxn][maxn];   //二分图
int cx[maxn];           //表示左集合i顶点所匹配的右端点
int cy[maxn];           //右集合
int nx,ny,dx[maxn],dy[maxn],dis;
bool mark[maxn];
bool bfs(){
    queue<int>Q;
    dis=inf;
    memset(dx,-1,sizeof(dx));
    memset(dy,-1,sizeof(dy));
    for(int i=1;i<=nx;i++){
        if(cx[i]==-1)Q.push(i),dx[i]=0;
    }
    while(!Q.empty()){
        int u=Q.front();Q.pop();
        if(dx[u]>dis)break;
        for(int v=1;v<=ny;v++){
            if(bmap[u][v]&&dy[v]==-1){
                dy[v]=dx[u]+1;
                if(cy[v]==-1)dis=dy[v];
                else{
                    dx[cy[v]]=dy[v]+1;
                    Q.push(cy[v]);
                }
            }
        }
    }
    return dis!=inf;
}
int dfs(int u){
    for(int v=1;v<=ny;v++){
        if(!mark[v]&&bmap[u][v]&&dy[v]==dx[u]+1){
            mark[v]=1;
            if(cy[v]!=-1&&dy[v]==dis)continue;
            if(cy[v]==-1||dfs(cy[v])){
                cy[v]=u;cx[u]=v;
                return 1;
            }
        }
    }
    return 0;
}
int MaxMatch(){
    int res=0;
    memset(cx,-1,sizeof(cx));
    memset(cy,-1,sizeof(cy));
    while(bfs()){
        memset(mark,0,sizeof(mark));
        for(int i=1;i<=nx;i++){
            if(cx[i]==-1)res+=dfs(i);
        }
    }
    return res;
}

二分图最大基数匹配

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
/// 二分图最大基数匹配
struct BPM{
    int n,m;    /// 左右顶点个数
    vector<int>G[maxn]; /// 邻接表
    int left[maxn];    /// left[i]为右边第i个点的匹配点编号，-1表示不存在
    bool T[maxn];       /// T[i]为右边第i个点是否已标记

    int right[maxn];        /// 求最小覆盖用
    bool S[maxn];           /// 求最小覆盖用

    void init(int n,int m){
        this->n=n;
        this->m=m;
        for(int i=0;i<n;i++)G[i].clear();
    }

    void AddEdge(int u,int v){
        G[u].push_back(v);
    }

    bool match(int u){
        S[u]=true;
        for(int i=0;i<G[u].size();i++){
            int v=G[u][i];
            if(!T[v]){
                T[v]=true;
                if(left[v]==-1||match(left[v])){
                    left[v]=u;
                    right[u]=v;
                    return true;
                }
            }
        }
        return false;
    }
    /// 求最大匹配
    int solve(){
        memset(left,-1,sizeof(left));
        memset(right,-1,sizeof(right));
        int ans=0;
        for(int u=0;u<n;u++){
            memset(S,0,sizeof(S));
            memset(T,0,sizeof(T));
            if(match(u))ans++;
        }
        return ans;
    }
    /// 求最小覆盖。X和Y为最小覆盖中的点集
    int mincover(vector<int>& X,vector<int>& Y){
        int ans=solve();
        memset(S,0,sizeof(S));
        memset(T,0,sizeof(T));
        for(int u=0;u<n;u++)
            if(right[u]==-1)match(u);
        for(int u=0;u<n;u++)
            if(!S[u])X.push_back(u);
        for(int v=0;v<n;v++)
            if(T[v])Y.push_back(v);
        return ans;
    }
};

二分图最大权匹配(KM算法)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
int g[150][150];  ///存图
int nx,ny; /// 两边点数
bool visx[maxn],visy[maxn];
int slack[maxn];
int linker[maxn];   ///y中各点匹配状态
int lx[maxn],ly[maxn]; /// x,y中的点标号
bool dfs(int x){
    visx[x]=true;
    for(int y=0;y<ny;y++){
        if(visy[y])continue;
        int tmp=lx[x]+ly[y]-g[x][y];
        if(tmp==0){
            visy[y]=true;
            if(linker[y]==-1||dfs(linker[y])){
                linker[y]=x;return true;
            }
        }
        else if(slack[y]>tmp)slack[y]=tmp;
    }
    return false;
}
int KM(){
    memset(linker,-1,sizeof(linker));
    memset(ly,0,sizeof(ly));
    for(int i=0;i<nx;i++){
        lx[i]=-inf;
        for(int j=0;j<ny;j++){
            if(g[i][j]>lx[i])lx[i]=g[i][j];
        }
    }
    for(int x=0;x<nx;x++){
        for(int i=0;i<ny;i++)slack[i]=inf;
        while(true){
            memset(visx,false,sizeof(visx));
            memset(visy,false,sizeof(visy));
            if(dfs(x))break;
            int d=inf;
            for(int i=0;i<ny;i++)
                if(!visy[i]&&d>slack[i])d=slack[i];
            for(int i=0;i<nx;i++)
                if(visx[i])lx[i]-=d;
            for(int i=0;i<ny;i++)
                if(visy[i])ly[i]+=d;
                else slack[i]-=d;
        }
    }
    int res=0;
    for(int i=0;i<ny;i++)
        if(linker[i]!=-1)res+=g[linker[i]][i];
    return res;
}

bfs实现的KM

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
const int N=2e2+50;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
int val[N][N];
ll lx[N],ly[N];
int linky[N];
ll pre[N];
bool vis[N];
bool visx[N],visy[N];
ll slack[N];
int n;
void bfs(int k){
    ll px, py = 0,yy = 0, d;
    memset(pre, 0, sizeof(ll) * (n+2));
    memset(slack, inf, sizeof(ll) * (n+2));
    linky[py]=k;
    do{
        px = linky[py],d = INF, vis[py] = 1;
        for(int i = 1; i <= n; i++)
            if(!vis[i]){
                if(slack[i] > lx[px] + ly[i] - val[px][i])
                    slack[i] = lx[px] + ly[i] -val[px][i], pre[i]=py;
                if(slack[i]<d) d=slack[i],yy=i;
            }
        for(int i = 0; i <= n; i++)
            if(vis[i]) lx[linky[i]] -= d, ly[i] += d;
            else slack[i] -= d;
        py = yy;
    }while(linky[py]);
    while(py) linky[py] = linky[pre[py]] , py=pre[py];
}
void KM(){
    memset(lx, 0, sizeof(int)*(n+2));
    memset(ly, 0, sizeof(int)*(n+2));
    memset(linky, 0, sizeof(int)*(n+2));
    for(int i = 1; i <= n; i++)
        memset(vis, 0, sizeof(bool)*(n+2)), bfs(i);
}
        ll ans=0;
        KM();
        for(int i=1;i<=n;i++)ans+=lx[i]+ly[i];

网络流

理论

建模技巧

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
##二分图带权最大独立集。
给出一个二分图，每个结点上有一个正权值。要求选出一些点，使得这些点之间没有边相连，且权值和最大。

解：在二分图的基础上添加源点 S 和汇点 T，然后从 S 向所有 X 集合中的点连一条边，所有 Y 集合中的点向 T 连一条边，容量均为该点的权值。X 结点与 Y 结点之间的边的容量均为无穷大。这样，对于图中的任意一个割，将割中的边对应的结点删掉就是一个符合要求的解，权和为所有权减去割的容量。因此，只需要求出最小割，就能求出最大权和。

##公平分配问题。
把 m 个任务分配给 n 个处理器。其中每个任务有两个候选处理器，可以任选一个分配。要求所有处理器中，任务数最多的那个处理器所分配的任务数尽量少。不同任务的候选处理器集 {p1, p2} 保证不同。

解：本题有一个比较明显的二分图模型，即 X 结点是任务，Y 结点是处理器。二分答案 x，然后构图，首先从源点S 出发向所有的任务结点引一条边，容量等于 1，然后从每个任务结点出发引两条边，分别到达它所能分配到的两个处理器结点，容量为 1，最后从每个处理器结点出发引一条边到汇点 T，容量为 x，表示选择该处理器的任务不能超过 x。这样网络中的每个单位流量都是从 S 流到一个任务结点，再到处理器结点，最后到汇点 T。只有当网络中的总流量等于
m 时才意味着所有任务都选择了一个处理器。这样，我们通过 O(log m) 次最大流便算出了答案。

##区间 k 覆盖问题。
数轴上有一些带权值的左闭右开区间。选出权和尽量大的一些区间，使得任意一个数最多被 k 个区间覆盖
解：本题可以用最小费用流解决，构图方法是把每个数作为一个结点，然后对于权值为 w 的区间 [u, v) 加边 u→v，容量为 1，费用为 −w。再对所有相邻的点加边 i→i + 1，容量为 k，费用为 0。最后，求最左点到最右点的最小费用最大流即可，其中每个流量对应一组互不相交的区间。如果数值范围太大，可以先进行离散化。

##最大闭合子图。
给定带权图 G（权值可正可负），求一个权和最大的点集，使得起点在该点集中的任意弧，终点也在该点集中。
解：新增附加源 s 和附加汇 t，从 s 向所有正权点引一条边，容量为权值；从所有负权点向汇点引一条边，容量为权值的相反数。求出最小割以后，S − {s} 就是最大闭合子图。

##最大密度子图。
给出一个无向图，找一个点集，使得这些点之间的边数除以点数的值（称为子图的密度）最大。
解：如果两个端点都选了，就必然要选边，这就是一种推导。如果把每个点和每条边都看成新图中的结点，可以把问题转化为最大闭合子图。

假设答案为k ，则要求解的问题是：边/点=K最大
选出一个合适的点集 V 和边集 E，令(|E|−k∗|V|)取得最大值。
所谓“合适”是指满足如下限制：若选择某条边，则必选择其两端点。
建图:
以原图的边作为左侧顶点，权值为1；
原图的点作为右侧顶点，权值为+k。
若原图中存在边 (u,v)，则新图中添加两条边 ([uv]−>u),([uv]−>v)，转换为最大权闭合子图。

## 二分图的最小点权覆盖集算法
在原图点集的基础上增加源 和汇 ；将每条二分图的边 s ,u v E ∈t 替换为容量=∞的有向边 , 把所有的X连线源，所有的Y连线汇容量为点权，

## 最大点权独立集 = V-最小点权覆盖

上下界网络流建图方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
## 记号说明
• f(u, v) 表示 u → v 的实际流量
• b(u, v) 表示 u → v 的流量下界
• c(u, v) 表示 u → v 的流量上界
##无源汇可行流
 建图
	• 新建附加源点 S 和 T
	• 原图中的边 u → v，限制为 [b, c]，建边 u → v，容量为 c − b
	• 记 d(i) = ∑b(u, i) −∑b(i, v)
	• 若 d(i) > 0，建边 S → i，流量为 d(i)
	• 若 d(i) < 0，建边 i → T，流量为 −d(i)
   
求解
	• 跑 S → T 的最大流，如果满流，则原图存在可行流。
	• 此时，原图中每一条边的流量为新图中对应边的流量加上这条边的下界。
	
##有源汇可行流
建图
	• 在原图中建边 t → s，流量限制为 [0, +∞)，这样就改造成了无源汇的网络流图。
	• 之后就可以像求解无源汇可行流一样建图了。
求解 同无源汇可行流

##有源汇最大流
建图 同有源汇可行流
求解
	• 先跑一遍 S → T 的最大流，求出可行流
	• 记此时 ∑f(s, i) = sum1
	• 将 t → s 这条边拆掉，在新图上跑 s → t 的最大流
	• 记此时 ∑f(s, i) = sum2
	• 最终答案即为 sum1 + sum2
##有源汇最小流
建图 同有源汇可行流
求解
	• 先跑一遍 S → T 的最大流，求出可行流
	• 记此时 ∑f(s, i) = sum1
	• 将 t → s 这条边拆掉，在新图上跑 t → s 的最大流f
	• 最终答案即为 sum1 - f
	这个可以理解成通过最大化退流量来使得流量最小。
##有源汇费用流
建图
	• 新建附加源点 S 和 T
	• 原图中的边 u → v，限制为 [b, c]，费用为 cost，建边 u → v，容量为 c − b，费用为 cost
• 记 d(i) = ∑b(u, i) −
∑b(i, v)
	• 若 d(i) > 0，建边 S → i，流量为 d(i)，费用为 0
	• 若 d(i) < 0，建边 i → T，流量为 −d(i)，费用为 0
	• 建边 t → s，流量为 +∞，费用为 0。
求解
	• 跑 S → T 的最小费用最大流
	• 答案为求出的费用加上原图中边的下界乘以边的费用

Edge

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
struct Edge
{
    int from, to, cap, flow;
    Edge(int u, int v, int c, int f)
        : from(u), to(v), cap(c), flow(f) {}
};
// ---
// 费用流
// ---
struct Edge
{
    int from, to, cap, flow, cost;
    Edge(int u, int v, int c, int f, int w)
        : from(u), to(v), cap(c), flow(f), cost(w) {}
};

EdmondKarp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
const int maxn = "Edit";
struct EdmonsKarp //时间复杂度O(v*E*E)
{
    int n, m;
    vector<Edge> edges;  //边数的两倍
    vector<int> G[maxn]; //邻接表，G[i][j]表示节点i的第j条边在e数组中的序号
    int a[maxn];         //起点到i的可改进量
    int p[maxn];         //最短路树上p的入弧编号
    void init(int n)
    {
        for (int i = 0; i < n; i++) G[i].clear();
        edges.clear();
    }
    void AddEdge(int from, int to, int cap)
    {
        edges.emplace_back(from, to, cap, 0);
        edges.emplace_back(to, from, 0, 0); //反向弧
        m = edges.size();
        G[from].push_back(m - 2);
        G[to].push_back(m - 1);
    }
    int Maxflow(int s, int t)
    {
        int flow = 0;
        for (;;)
        {
            memset(a, 0, sizeof(a));
            queue<int> q;
            q.push(s);
            a[s] = INF;
            while (!q.empty())
            {
                int x = q.front();
                q.pop();
                for (int i = 0; i < G[x].size(); i++)
                {
                    Edge& e = edges[G[x][i]];
                    if (!a[e.to] && e.cap > e.flow)
                    {
                        p[e.to] = G[x][i];
                        a[e.to] = min(a[x], e.cap - e.flow);
                        q.push(e.to);
                    }
                }
                if (a[t]) break;
            }
            if (!a[t]) break;
            for (int u = t; u != s; u = edges[p[u]].from)
            {
                edges[p[u]].flow += a[t];
                edges[p[u] ^ 1].flow -= a[t];
            }
            flow += a[t];
        }
        return flow;
    }
};

Dinic

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
const int maxn = "Edit";
struct Dinic
{
    int n, m, s, t;      //结点数，边数（包括反向弧），源点编号和汇点编号
    vector<Edge> edges;  //边表。edge[e]和edge[e^1]互为反向弧
    vector<int> G[maxn]; //邻接表，G[i][j]表示节点i的第j条边在e数组中的序号
    bool vis[maxn];      //BFS使用
    int d[maxn];         //从起点到i的距离
    int cur[maxn];       //当前弧下标
    void init(int n)
    {
        this->n = n;
        for (int i = 0; i < n; i++) G[i].clear();
        edges.clear();
    }
    void AddEdge(int from, int to, int cap)
    {
        edges.emplace_back(from, to, cap, 0);
        edges.emplace_back(to, from, 0, 0);
        m = edges.size();
        G[from].push_back(m - 2);
        G[to].push_back(m - 1);
    }
    bool BFS()
    {
        memset(vis, 0, sizeof(vis));
        memset(d, 0, sizeof(d));
        queue<int> q;
        q.push(s);
        d[s] = 0;
        vis[s] = 1;
        while (!q.empty())
        {
            int x = q.front();
            q.pop();
            for (int i = 0; i < G[x].size(); i++)
            {
                Edge& e = edges[G[x][i]];
                if (!vis[e.to] && e.cap > e.flow)
                {
                    vis[e.to] = 1;
                    d[e.to] = d[x] + 1;
                    q.push(e.to);
                }
            }
        }
        return vis[t];
    }
    int DFS(int x, int a)
    {
        if (x == t || a == 0) return a;
        int flow = 0, f;
        for (int& i = cur[x]; i < G[x].size(); i++)
        { //从上次考虑的弧
            Edge& e = edges[G[x][i]];
            if (d[x] + 1 == d[e.to] && (f = DFS(e.to, min(a, e.cap - e.flow))) > 0)
            {
                e.flow += f;
                edges[G[x][i] ^ 1].flow -= f;
                flow += f;
                a -= f;
                if (a == 0) break;
            }
        }
        return flow;
    }
    int Maxflow(int s, int t)
    {
        this->s = s, this->t = t;
        int flow = 0;
        while (BFS())
        {
            memset(cur, 0, sizeof(cur));
            flow += DFS(s, INF);
        }
        return flow;
    }
    vector<int>Mincut(){ /// call this after maxflow
        vector<int>ans;
        for(int i=0;i<edges.size();i++){
            Edge& e=edges[i];
            if(vis[e.from]&&!vis[e.to]&&e.cap>0)ans.push_back(i);
        }
        return ans;
    }
};

ISAP

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
const int maxn = "Edit";
struct ISAP
{
    int n, m, s, t;      //结点数，边数（包括反向弧），源点编号和汇点编号
    vector<Edge> edges;  //边表。edges[e]和edges[e^1]互为反向弧
    vector<int> G[maxn]; //邻接表，G[i][j]表示结点i的第j条边在e数组中的序号
    bool vis[maxn];      //BFS使用
    int d[maxn];         //起点到i的距离
    int cur[maxn];       //当前弧下标
    int p[maxn];         //可增广路上的一条弧
    int num[maxn];       //距离标号计数
    void init(int n)
    {
        this->n = n;
        for (int i = 0; i < n; i++) G[i].clear();
        edges.clear();
    }
    void AddEdge(int from, int to, int cap)
    {
        edges.emplace_back(from, to, cap, 0);
        edges.emplace_back(to, from, 0, 0);
        int m = edges.size();
        G[from].push_back(m - 2);
        G[to].push_back(m - 1);
    }
    int Augumemt()
    {
        int x = t, a = INF;
        while (x != s)
        {
            Edge& e = edges[p[x]];
            a = min(a, e.cap - e.flow);
            x = edges[p[x]].from;
        }
        x = t;
        while (x != s)
        {
            edges[p[x]].flow += a;
            edges[p[x] ^ 1].flow -= a;
            x = edges[p[x]].from;
        }
        return a;
    }
    void BFS()
    {
        memset(vis, 0, sizeof(vis));
        memset(d, 0, sizeof(d));
        queue<int> q;
        q.push(t);
        d[t] = 0;
        vis[t] = 1;
        while (!q.empty())
        {
            int x = q.front();
            q.pop();
            int len = G[x].size();
            for (int i = 0; i < len; i++)
            {
                Edge& e = edges[G[x][i] ^ 1];
                if (!vis[e.from] && e.cap > e.flow)
                {
                    vis[e.from] = 1;
                    d[e.from] = d[x] + 1;
                    q.push(e.from);
                }
            }
        }
    }
    int Maxflow(int s, int t)
    {
        this->s = s;
        this->t = t;
        int flow = 0;
        BFS();
        memset(num, 0, sizeof(num));
        for (int i = 0; i < n; i++)
            if (d[i] < INF) num[d[i]]++;
        int x = s;
        memset(cur, 0);
        while (d[s] < n)
        {
            if (x == t)
            {
                flow += Augumemt();
                x = s;
            }
            int ok = 0;
            for (int i = cur[x]; i < G[x].size(); i++)
            {
                Edge& e = edges[G[x][i]];
                if (e.cap > e.flow && d[x] == d[e.to] + 1)
                {
                    ok = 1;
                    p[e.to] = G[x][i];
                    cur[x] = i;
                    x = e.to;
                    break;
                }
            }
            if (!ok) //Retreat
            {
                int m = n - 1;
                for (int i = 0; i < G[x].size(); i++)
                {
                    Edge& e = edges[G[x][i]];
                    if (e.cap > e.flow) m = min(m, d[e.to]);
                }
                if (--num[d[x]] == 0) break; //gap优化
                num[d[x] = m + 1]++;
                cur[x] = 0;
                if (x != s) x = edges[p[x]].from;
            }
        }
        return flow;
    }
};

MinCost MaxFlow

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
const int maxn = "Edit";
struct MCMF
{
    int n, m;
    vector<Edge> edges;
    vector<int> G[maxn];
    int inq[maxn]; //是否在队列中
    int d[maxn];   //bellmanford
    int p[maxn];   //上一条弧
    int a[maxn];   //可改进量
    void init(int n)
    {
        this->n = n;
        for (int i = 0; i < n; i++) G[i].clear();
        edges.clear();
    }
    void AddEdge(int from, int to, int cap, int cost)
    {
        edges.emplace_back(from, to, cap, 0, cost);
        edges.emplace_back(to, from, 0, 0, -cost);
        m = edges.size();
        G[from].push_back(m - 2);
        G[to].push_back(m - 1);
    }
    bool BellmanFord(int s, int t, int& flow, ll& cost)
    {
        for (int i = 0; i < n; i++) d[i] = INF;
        memset(inq, 0, sizeof(inq));
        d[s] = 0;
        inq[s] = 1;
        p[s] = 0;
        a[s] = INF;
        queue<int> q;
        q.push(s);
        while (!q.empty())
        {
            int u = q.front();
            q.pop();
            inq[u] = 0;
            for (int i = 0; i < G[u].size(); i++)
            {
                Edge& e = edges[G[u][i]];
                if (e.cap > e.flow && d[e.to] > d[u] + e.cost)
                {
                    d[e.to] = d[u] + e.cost;
                    p[e.to] = G[u][i];
                    a[e.to] = min(a[u], e.cap - e.flow);
                    if (!inq[e.to])
                    {
                        q.push(e.to);
                        inq[e.to] = 1;
                    }
                }
            }
        }
        if (d[t] == INF) return false; // 当没有可增广的路时退出
        flow += a[t];
        cost += (ll)d[t] * (ll)a[t];
        for (int u = t; u != s; u = edges[p[u]].from)
        {
            edges[p[u]].flow += a[t];
            edges[p[u] ^ 1].flow -= a[t];
        }
        return true;
    }
    int MincostMaxflow(int s, int t, ll& cost)
    {
        int flow = 0;
        cost = 0;
        while (BellmanFord(s, t, flow, cost));
        return flow;
    }
};

sap

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+50;
int S,T,From[maxn],Laxt[maxn],Next[maxn],To[maxn],Cap[maxn],cnt;
int vd[maxn],dis[maxn];
void add(int u,int v,int c){
    Next[++cnt]=Laxt[u];Laxt[u]=cnt;To[cnt]=v;Cap[cnt]=c;From[cnt]=u;
    Next[++cnt]=Laxt[v];Laxt[v]=cnt;To[cnt]=u;Cap[cnt]=0;From[cnt]=v;
}
int sap(int u,int flow,int limit){
    if(u==T||flow==0)return flow;
    int tmp,delta=0;
    for(int i=Laxt[u];i;i=Next[i]){
        int v=To[i];
        if(dis[u]==dis[v]+1&&Cap[i]){
            tmp=sap(v,min(flow-delta,Cap[i]),limit);
            Cap[i]-=tmp;Cap[i^1]+=tmp;delta+=tmp;
            if(dis[S]>=(limit)||delta==flow)return delta;
        }
    }
    vd[dis[u]]--;if(!vd[dis[u]])dis[S]=limit;
    vd[++dis[u]]++;
    return delta;
}
void init(int limit){
    cnt=1;
    for(int i=0;i<=limit;i++)Laxt[i]=dis[i]=vd[i]=0;
}

LCA

倍增

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
struct LCA{
    int n;
    int fa[maxn];       ///父亲数组
    int cost[maxn];     ///和父亲的费用
    int L[maxn];        ///层次(根节点为0)
    int anc[maxn][logmaxn];     /// anc[p][i]是结点p的第2^i级父亲。anc[i][0] = fa[i]
    int maxcost[maxn][logmaxn]; /// maxcost[p][i]是i和anc[p][i]的路径上的最大费用
    void preprocess(){
        for(int i=0;i<n;i++){
            anc[i][0]=fa[i];maxcost[i][0]=cost[i];
            for(int j=1;(1<<j)<n;j++)anc[i][j]=-1;
        }
        for(int j=1;(1<<j)<n;j++)
            for(int i=0;i<n;i++)
        if(anc[i][j-1]!=-1){
            int a=anc[i][j-1];
            anc[i][j]=anc[a][j-1];
            maxcost[i][j]=max(maxcost[i][j-1],maxcost[a][j-1]);
        }
    }
    /// 求p到q的路径上的最大权
    int query(int p,int q){
        int tmp,log,i;
        if(L[p]<L[q])swap(p,q);
        for(log=1;(1<<log)<=L[p];log++);log--;
        int ans=-inf;
        for(int i=log;i>=0;i--)
        if(L[p]-(1<<i)>=L[q]){ans=max(ans,maxcost[p][i]);p=anc[p][i];}

        if(p==q)return ans; ///LCA为p

        for(int i=log;i>=0;i--)
        if(anc[p][i]!=-1&&anc[p][i]!=anc[q][i]){
            ans=max(ans,maxcost[p][i]);p=anc[p][i];
            ans=max(ans,maxcost[q][i]);q=anc[q][i];
        }
        ans=max(ans,cost[p]);
        ans=max(ans,cost[q]);
        return ans; ///LCA为fa[p]（它也等于fa[q]）
    }
};

倍增简单写法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
int mi[maxn][22],fa[maxn][22],dep[maxn];
void dfs(int now,int pre,int w,int deep){
    fa[now][0]=pre;
    mi[now][0]=w;
    if(pre==0)mi[now][0]=inf,fa[now][0]=now;
    dep[now]=deep;
    for(auto i:ve[now]){
        if(i.to==pre)continue;
        dfs(i.to,now,i.w,deep+1);
    }
}
void init(){
    for(int i=1;i<=20;i++)
    for(int j=1;j<=n;j++){
        int p=fa[j][i-1];
        fa[j][i]=fa[p][i-1];
        mi[j][i]=min(mi[j][i-1],mi[p][i-1]);
    }
}
int lca(int p,int q){
    if(dep[p]<dep[q])swap(p,q);
    int res=inf;
    for(int i=20;i>=0;i--)
        if(dep[fa[p][i]]>=dep[q])
        res=min(res,mi[p][i]),p=fa[p][i];
    if(p==q)return res;
    for(int i=20;i>=0;i--){
        if(fa[p][i]!=fa[q][i]){
            res=min(res,mi[p][i]);
            res=min(res,mi[q][i]);
            p=fa[p][i];q=fa[q][i];
        }
    }
    return min(res,min(mi[p][0],mi[q][0]));
}

RMQ写法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
int d[maxn*2][20],dep[maxn],id[maxn],w[maxn],cnt; ///空间要开两倍多
int n,sum,rt,f[maxn],vis[maxn],luo,sz[maxn];
void init(){
    for(int i=1;i<=n;i++)
        G[i].clear(),vis[i]=f[i]=0;
    cnt=0;
}
void dfs(int u,int fa){
    dep[u]=dep[fa]+1;
    d[++cnt][0] = dep[u];
    id[u] = cnt;
    for(auto v:G[u]){
        if(v==fa)continue;
        dfs(v, u);
        d[++cnt][0]=dep[u];
    }
}
void rmq_init(){
    for(int i=1;i<=18;i++)
        for(int j=1;j+(1<<i)-1<=cnt;j++)
            d[j][i]=min(d[j][i-1],d[j+(1<<i-1)][i-1]);
}
int LCA(int x,int y){
    int l=id[x],r=id[y];
    if(l>r)swap(l,r);
    int k=log2(r-l+1);
    return min(d[l][k],d[r+1-(1<<k)][k]);
}
int dis(int x,int y){
    return dep[x]+dep[y]-2*LCA(x,y);
}

树上差分

点差分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//查询每个点没经过的次数
int sum[maxn],mx;
int dfs1(int u,int p){
    for(int i=Laxt[u];i;i=Next[i]){
        int v=To[i];if(v==p)continue;
        dfs1(v,u);sum[u]+=sum[v];
    }
    if(sum[u]>mx)mx=sum[u];
}
while(k--){
        int u,v;
        cin>>u>>v;
        sum[u]++;sum[v]++;
        int p=lca(u,v);
        sum[p]--;
        sum[fa[p][0]]--;
    }
dfs1(1,0);

边差分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
//查询每个边的经过次数
//边传递给后一个节点
void dfs(int u,int pre){
    for(int i=Laxt[u];i;i=Next[i]){
        int v=To[i];
        if(v==pre)continue;
        dfs(v,u);
        num[u]+=num[v];
    }
}
bool check(int x){
    int k=0,now=0;
    for(int i=1;i<=n;i++)num[i]=0;
    for(int i=1;i<=m;i++){
        if(my[i].w<=x)continue;
        num[my[i].u]++;num[my[i].v]++;num[my[i].lca]-=2;
        k++;
    }
    dfs(1,0);
    for(int i=1;i<=n;i++)if(num[i]==k)now=max(now,value[i]);
    return my[m].w-now<=x;
}

数学

拉格朗日插值

普通n^2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
ll n,k;
x[1]=1;x[2]=2;x[3]=3;x[4]=4;x[5]=5;
y[1]=1;y[2]=5;y[3]=15;y[4]=35;y[5]=70;
int t;n=5;
cin>>t;
while(t--){
    cin>>k;
    ll ans=0;
    for(int i=1;i<=n;i++){
        ll fz=y[i];
        ll fm=1;
        for(int j=1;j<=n;j++){
            if(i==j)continue;
            fz=fz*(k-x[j])%mod;
            fm=fm*(x[i]-x[j])%mod;
        }
        ans+=fz*ksm(fm,mod-2)%mod;
        ans%=mod;
        ans+=mod;ans%=mod;
    }
    cout<<ans<<endl;
}

x取连续时的插值法 复杂度O(n)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
 
int pv[]={0,1,5,15,35,70}; //前几项, 前面无效值用0占位
const int st=1,ed=5;           //使用上面数组下标为[st,ed]的数据
 
ll fac[ed+5],inv[ed+5],facinv[ed+5];
ll pre[ed+5],saf[ed+5];
 
//预处理: fac[]阶乘, inv[]逆元, facinv[]阶乘逆元
//只需要main函数内调用一次!
void init()
{
    fac[0]=inv[0]=facinv[0]=1;
    fac[1]=inv[1]=facinv[1]=1;
    for(int i=2;i<ed+3;++i)
    {
        fac[i]=fac[i-1]*i%mod;
        inv[i]=mod-(mod/i*inv[mod%i]%mod);
        facinv[i]=facinv[i-1]*inv[i]%mod;
    }
}
 
 
//计算第x0项的值
//复杂度O(ed-st)
ll cal(ll x0)
{
    int n=ed-st;
    x0=((x0%mod)+mod)%mod;
    pre[0]=((x0-st)%mod+mod)%mod;
    saf[n]=((x0-st-n)%mod+mod)%mod;
    for(int i=1;i<=n;++i)
    {
        pre[i]=((pre[i-1]*(x0-st-i))%mod+mod)%mod;
        saf[n-i]=((saf[n-i+1]*(x0-st-n+i))%mod+mod)%mod;
    }
    ll res=0;
    for(int i=0;i<=n;++i)
    {
        ll fz=1;
        if(i!=0)fz=fz*pre[i-1]%mod;
        if(i!=n)fz=fz*saf[i+1]%mod;
        ll fm=facinv[i]*facinv[n-i]%mod;
        if((n-i)&1)fm=mod-fm;
        (res+=pv[i+st]*(fz*fm%mod)%mod)%=mod;
    }
    return res;
}
 
int main()
{
    init();
    int t,n;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        printf("%d\n",cal(n));
    }
 
}

差分表

一些公式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//平方和公式 sigm（i^2）=n*(n+1)*(2n+1)/6
//皮克定理 多边形面积S = 多边形内整数点的个数 n + 多边形边上整数点的个数 / 2 - 1 
//边界的点数用gcd(a.x-b.x,a.y-b.y)计算
//当O点为原点时，根据向量的叉积计算公式，各个三角形的面积计算如下：
//S_OAB = 0.5*(A_x*B_y - A_y*B_x)   【(A_x，A_y)为A点的坐标】
//S_OBC = 0.5*(B_x*C_y - B_y*C_x)
/*
斯特林公式
 int digit_stirling(int n)///求n！的位数
{
     double PI=acos(double(-1));// PI的值=反余弦函数 -1.0为Pi， 1为0。
     double e=exp(double(1));//e的值
     return floor(log10(sqrt(2*PI*n))+n*log10(n/e))+1;
}
*/
//G[X]表示：1-X的数字和的总和；

//根据G[10^X]=45*X*10^(X-1);所以G[10^18]=45*18*10^17;
//等差数列求和：Sn=n*a1+n(n-1)d/2或Sn=n(a1+an)/2
//等比数列求和：Sn=a1*(1-q^n)/(1-q)=(a1-an*q)/(1-q)

莫比乌斯反演

组合数计数

1
2
3
4
5
6
7
8
    inv[0]=p[0]=1;
    for(int i=1;i<=n;i++)
        p[i]=p[i-1]*i%mod,inv[i]=ksm(p[i],mod-2);
}
ll cal(int n,int m){
    if(n<m)return 0LL;
    return p[n]*inv[n-m]%mod*inv[m]%mod;
}

卢卡斯定理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
ll pow_mod(ll x, ll n, ll mod){
    ll res=1;
    while(n){
        if(n&1)res=res*x%mod;
        x=x*x%mod;
        n>>=1;
    }
    return res;
}
ll inv(ll a,ll p){return pow_mod(a,p-2,p);}
ll cal(ll a,ll b,ll p){
    if(a<b)return 0;
    if(b>a-b)b=a-b;
    ll fz=1,fm=1;
    for(ll i=0;i<b;i++){
        fz=fz*(a-i)%p;
        fm=fm*(i+1)%p;
    }
    return fz*inv(fm,p)%p;
}

ll lucas(ll a,ll b,ll p){
    if(b==0)return 1;
    return cal(a%p,b%p,p)*lucas(a/p,b/p,p)%p;
}

逆元

如果mod不是素数 那么a关于mod的逆元是 a^(phi(mod)-1)

ExGcd求逆元

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
///返回 d=gcd(a,b); 和对应于等式 ax+by=d 中的 x,y
ll extend_gcd(ll a,ll b,ll &x,ll &y){
    if(a==0&&b==0)return -1;
    if(b==0){x=1;y=0;return a;}
    ll d=extend_gcd(b,a%b,y,x);
    y-=a/b*x;
    return d;
}
///ax=1(mod n)
ll mod_reverse(ll a,ll n){
    ll x,y;
    ll d=extend_gcd(a,n,x,y);
    if(d==1)return (x%n+n)%n;
    else return -1;
}

费马小定理

1
2
3
4
5
6
7
8
9
10
11
///a<mod 并且 p为素数
ll pow_mod(ll x, ll n, ll mod){
    ll res=1;
    while(n){
        if(n&1)res=res*x%mod;
        x=x*x%mod;
        n>>=1;
    }
    return res;
}
ll inv(ll a,ll p){return pow_mod(a,p-2,p);}

逆元线性筛

1
2
inv[1]=1;
for (int i = 2; i < maxn; i++) inv[i] = inv[p % i] * (p - p / i) % p;

杜教筛

设需要计算的式子为：$[Math Processing Error]\sum_{i=1}^{n}f(i)（f(i)为积性函数）$

我们构造两个积性函数$h$和$g$。使得$h=f∗g$

现在我们开始求$\sum_{i=1}^{n}h(i)$

记$[Math Processing Error]S(n)=\sum_{i=1}^{n}f(i)$

$\sum_{i=1}^{n}h(i)=\sum_{i=1}^{n}\sum_{d|i}g(d)\cdot f(\frac{i}{d})\\\to =\sum_{d=1}^{n}g(d)\cdot\sum_{i=1}^{\lfloor\frac{n}{d}\rfloor}f({i})$

$[Math Processing Error]\to \sum_{i=1}^{n}h(i)=\sum_{d=1}^{n}g(d)\cdot S(\lfloor\frac{n}{d}\rfloor)​$

接着，我们将右边式子的第一项给提出来，可以得到：

$\sum_{i=1}^{n}h(i)=g(1)\cdot S(n)+\sum_{d=2}^{n}g(d)\cdot S(\lfloor\frac{n}{d}\rfloor)$

$\to g(1)S(n)=\sum_{i=1}^{n}h(i)-\sum_{d=2}^{n}g(d)\cdot S(\lfloor\frac{n}{d}\rfloor) $

其中$h(i)=(f*g)(i)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=6e6+50;
unordered_map<int,int>m;
unordered_map<ll,ll>p;
bool vis[maxn];
int mu[maxn],sum_mu[maxn],phi[maxn];
ll sum_phi[maxn];
int cnt,prime[maxn];

void init(int N){
    phi[1]=mu[1]=1;
    for(int i=2;i<=N;i++){
        if(!vis[i]){
            prime[++cnt]=i;
            mu[i]=-1;phi[i]=i-1;
        }
        for(int j=1;j<=cnt;j++){
            if(i*prime[j]>N)break;
            vis[i*prime[j]]=true;
            if(i%prime[j]==0){
                phi[i*prime[j]]=phi[i]*prime[j];
                break;
            }
            mu[i*prime[j]]=-mu[i];
            phi[i*prime[j]]=phi[i]*(prime[j]-1);
        }
    }
    for(int i=1;i<=N;i++){
        sum_mu[i]=sum_mu[i-1]+mu[i];
        sum_phi[i]=sum_phi[i-1]+phi[i];
    }
}
int getmu(int x){
    if(x<=6e6)return sum_mu[x];
    if(m[x])return m[x];
    int ans=1;
    for(int l=2,r;l<=x;l=r+1){
        r=x/(x/l);
        ans-=(r-l+1)*getmu(x/l);
    }
    return m[x]=ans;
}
ll getphi(ll x){
    if(x<=6e6)return sum_phi[x];
    if(p[x])return p[x];
    ll ans=x*(x+1)/2;
    for(ll l=2,r;l<=x;l=r+1){
        r=x/(x/l);
        ans-=(r-l+1)*getphi(x/l);

    }
    return p[x]=ans;
}
int main(){
    int t,n;
    cin>>t;
    init(6e6);
    while(t--){
        cin>>n;
        cout<<getphi(n)<<" "<<getmu(n)<<endl;
    }
    return 0;
}

Lucy筛(素数个数 素数和)O(n^4/3)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#include<bits/stdc++.h>

using namespace std;
typedef long long ll;

ll check(ll v, ll n, ll ndr, ll nv) {
    return v >= ndr ? (n / v - 1) : (nv - v);
}

// ll S[10000000];
// ll V[10000000];
ll primenum(ll n) // O(n^(3/4))
{
  ll r = (ll)sqrt(n);
  ll ndr = n / r;
  assert(r*r <= n && (r+1)*(r+1) > n);
  ll nv = r + ndr - 1;
  std::vector<ll> S(nv+1);
  std::vector<ll> V(nv+1);
  for(ll i=0;i<r;i++) {
    V[i] = n / (i+1);
  }
  for(ll i=r;i<nv;i++) {
    V[i] = V[i-1] - 1;
  }
  for(ll i = 0;i<nv;i++) {
    S[i] = V[i] - 1; //求素数个数
  }
  for(ll p=2;p<=r;p++) {
    if(S[nv-p] > S[nv-p+1]) {
      ll sp = S[nv-p+1]; // sum of primes smaller than p
      ll p2 = p*p;
  //    std::cout << "p=" << p << '\n'; // p is prime 
      for(ll i=0;i<nv;i++) {
        if(V[i] >= p2) {
          S[i] -= 1LL  * (S[check(V[i] / p, n, ndr, nv)] - sp);// //求素数个数
        }
        else break;
      }
    }
  }
  return S[0];
}
ll primesum(ll n) // O(n^(3/4))
{
  ll r = (ll)sqrt(n);
  ll ndr = n / r;
  assert(r*r <= n && (r+1)*(r+1) > n);
  ll nv = r + ndr - 1;
  std::vector<ll> S(nv+1);
  std::vector<ll> V(nv+1);
  for(ll i=0;i<r;i++) {
    V[i] = n / (i+1);
  }
  for(ll i=r;i<nv;i++) {
    V[i] = V[i-1] - 1;
  }
  for(ll i = 0;i<nv;i++) {
    S[i] = V[i] * ( V[i] + 1) / 2 - 1; //求素数和
  }
  for(ll p=2;p<=r;p++) { // p is prime 
    if(S[nv-p] > S[nv-p+1]) {
      ll sp = S[nv-p+1]; // sum of primes smaller than p
      ll p2 = p*p; 
      for(ll i=0;i<nv;i++) {
        if(V[i] >= p2) {
        S[i] -= p* (S[check(V[i] / p, n, ndr, nv)] - sp); //求素数和
        }
        else break;
      }
    }
  }
  return S[0];
}
int main(int argc, char const *argv[]) {
//  std::cout << primesum(1e6) << '\n';
  std::cout << primenum(1e10) << '\n';
  std::cout << primesum(2e6) << '\n';
  cerr << "Time elapsed: " << 1.0 * clock() / CLOCKS_PER_SEC << " s.\n";
  return 0;
}

数论

数论函数基础

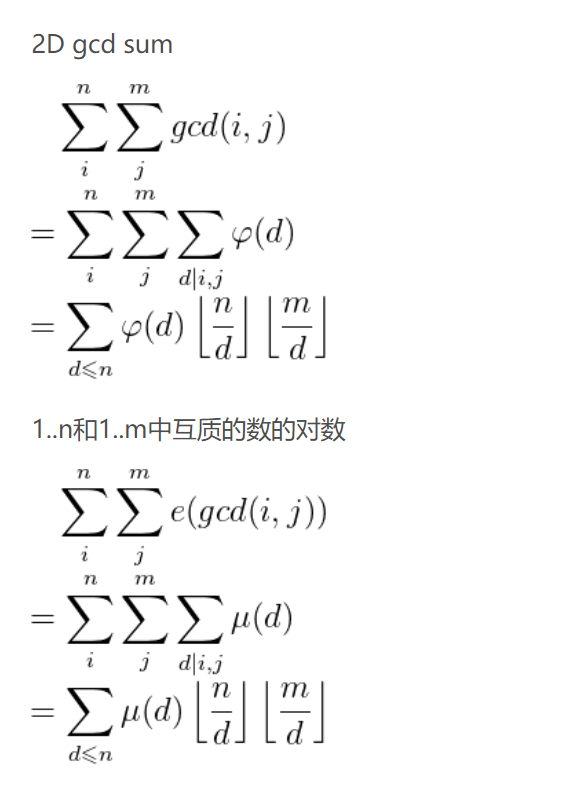
合数分解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
int prime[maxn+1];
void getprime(){
    memset(prime,0,sizeof(prime));
    for(int i=2;i<=maxn;i++){
        if(!prime[i])prime[++prime[0]]=i;
        for(int j=1;j<=prime[0]&&prime[j]<=maxn/i;j++){
            prime[prime[j]*i]=1;
            if(i%prime[j]==0)break;
        }
    }
}
ll factor[100][2];
int fatcnt;
int getfactors(ll x){
    fatcnt=0;
    ll tmp=x;
    for(int i=1;i<=prime[0]&&prime[i]<=tmp/prime[i];i++){
        factor[fatcnt][1]=0;
        if(tmp%prime[i]==0){
            factor[fatcnt][0]=prime[i];
            while(tmp%prime[i]==0){
                factor[fatcnt][1]++;
                tmp/=prime[i];
            }
            fatcnt++;
        }
    }
    if(tmp!=1){
        factor[fatcnt][0]=tmp;
        factor[fatcnt++][1]=1;
    }
    return fatcnt;
}

欧拉函数

欧拉降幂

A^Bmod C=A^(B mod phji(C)) %C gcd(a,c)==1

A^B mod C=A^B %C (B<phi(C))

A^B mod C=A^(B mod phi(C)+phi(C))%C (B>=phi(C))

得出单个数的欧拉函数 O(sqrt n)

1
2
3
4
5
6
7
8
9
10
11
12
ll euler(ll n)
{
    ll rt = n;
    for (int i = 2; i * i <= n; i++)
        if (n % i == 0)
        {
            rt -= rt / i;
            while (n % i == 0) n /= i;
        }
    if (n > 1) rt -= rt / n;
    return rt;
}

筛法欧拉函数

1
2
3
4
5
6
7
8
9
10
11
12
const int N = "Edit";
int phi[N] = {0, 1};
void caleuler()
{
    for (int i = 2; i < N; i++)
        if (!phi[i])
            for (int j = i; j < N; j += i)
            {
                if (!phi[j]) phi[j] = j;
                phi[j] = phi[j] / i * (i - 1);
            }
}

线性筛

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
bool check[maxn];
int phi[maxn];
int prime[maxn];
int tot;
void phi_and_prime_table(int N){
    memset(check,false,sizeof(check));
    phi[1]=1;
    tot=0;
    for(int i=2;i<=N;i++){
        if(!check[i]){
            prime[tot++]=i;
            phi[i]=i-1;
        }
        for(int j=0;j<tot;j++){
            if(i*prime[j]>N)break;
            check[i*prime[j]]=true;
            if(i%prime[j]==0){
                phi[i*prime[j]]=phi[i]*prime[j];
                break;
            }
            else{
                phi[i*prime[j]]=phi[i]*(prime[j]-1);
            }
        }
    }
}

莫比乌斯

莫比乌斯函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
int prime[maxn];
bool notprime[maxn];
int mu[maxn];
void getMobius(int N){
    mu[1]=1;    ///μ函数的1是特殊情况
    int tot=0;
    for(int i=2;i<=N;i++){
        if(!notprime[i]){
            prime[++tot]=i;
            mu[i]=-1;
        }
        for(int j=1;j<=tot;j++){
            if(i*prime[j]>N)break;
            notprime[i*prime[j]]=true;
            if(i%prime[j]==0){
                mu[i*prime[j]]=0;   ///i中已经包括了prime[j]
                break;
            }
            else{
                mu[i*prime[j]]=-mu[i];
            }
        }
    }
}

模线性方程

二次剩余

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
LL w;
struct Point{//x + y*sqrt(w)
    LL x;
    LL y;
};
LL mod(LL a, LL p){
    a %= p;
    if (a < 0){
        a += p;
    }
    return a;
}
Point point_mul(Point a, Point b, LL p){
    Point res;
    res.x = mod(a.x * b.x, p);
    res.x += mod(w * mod(a.y * b.y, p), p);
    res.x = mod(res.x, p);
    res.y = mod(a.x * b.y, p);
    res.y += mod(a.y * b.x, p);
    res.y = mod(res.y , p);
    return res;
}

Point power(Point a, LL b, LL p){
    Point res;
    res.x = 1;
    res.y = 0;
    while(b){
        if (b & 1){
            res = point_mul(res, a, p);
        }
        a = point_mul(a, a, p);
        b = b >> 1;
    }
    return res;
}

LL quick_power(LL a, LL b, LL p){//(a^b)%p
    LL res = 1;
    while(b){
        if (b & 1){
            res = (res * a) % p;
        }
        a = (a * a) % p;
        b = b >> 1;
    }
    return res;
}
LL Legendre(LL a, LL p){ // a^((p-1)/2)
    return quick_power(a, (p - 1) >> 1, p);
}

LL equation_solve(LL b, LL p){//求解x^2=b(%p)方程解
    if (b == 0)
        return 0;
    if ((Legendre(b, p) + 1) % p == 0){
        return -1;//表示没有解
    }
    LL a, t;
    while(true){
        a = rand() % p;
        t = a * a - b;
        t = mod(t, p);
        if ((Legendre(t, p) + 1) % p == 0){
            break;
        }
    }
    w = t;
    Point temp, res;
    temp.x = a;
    temp.y = 1;
    res = power(temp, (p + 1) >> 1, p);
    return res.x;
}

中国剩余定理

1
2
3
4
5
6
7
8
9
10
11
///要求m 两两互质 X=ri(mod mi) 引用返回通解 X=re+k*mo
void crt(ll r[],ll m[],ll n,ll &re,ll &mo){
    mo=1,re=0;
    for(int i=0;i<n;i++)mo*=m[i];
    for(int i=0;i<n;i++){
        ll x,y,tm=mo/m[i];
        ll d=exgcd(tm,m[i],x,y);
        re=(re+tm*x*r[i])%mo;
    }
    re=(re+mo)%mo;
}

ExCRT

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//mi可以不两两互质
bool excrt(ll r[], ll m[], ll n, ll &re, ll &mo)
{
    ll x, y;
    mo = m[0], re = r[0];
    for (int i = 1; i < n; i++)
    {
        ll d = exgcd(mo, m[i],  x, y);
        if ((r[i] - re) % d != 0) return 0;
        x = (r[i] - re) / d * x % (m[i] / d);
        re += x * mo;
        mo = mo / d * m[i];
        re %= mo;
    }
    re = (re + mo) % mo;
    return 1;
}

大步小步算法 a^x=b(mod n)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// 求解模方程a^x=b(mod n)。n 为素数。无解返回-1
int log_mod(int a, int b) {
  int m, v, e = 1, i;
  m = (int)sqrt(MOD);
  v = inv(pow_mod(a, m));
  map <int,int> x;
  x[1] = 0;
  for(i = 1; i < m; i++){ e = mul_mod(e, a); if (!x.count(e)) x[e] = i; }
  for(i = 0; i < m; i++){
    if(x.count(b)) return i*m + x[b];
    b = mul_mod(b, v);
  }
  return -1;
}

扩展大步小步(gcd!=1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
int ex_BSGS(int A,int B,int C)
{
    if(B==1) return 0;
    int k=0,tmp=1,d;
    while(1)
    {
        d=__gcd(A,C);
        if(d==1) break;
        if(B%d) return -1;
        B/=d; C/=d;
        tmp=1LL*tmp*(A/d)%C;
        k++;
        if(tmp==B) return k;
    }
    map<int,int>mp;
    mp.clear();
    int mul=B;
    mp[B]=0;
    int m=ceil(sqrt(1.0*C));
    for(int j=1;j<=m;++j)
    {
        mul=1LL*mul*A%C;
        mp[mul]=j;
    }
    int am=fastpow(A,m,C);
    mul=tmp;
    for(int j=1;j<=m;++j)
    {
        mul=1LL*mul*am%C;
        if(mp.count(mul)) return j*m-mp[mul]+k;
    }
    return -1;
}

线性基

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
struct Linear_Basis{
	long long d[65],p[65];
	int cnt;
	Linear_Basis(){
		memset(d,0,sizeof(d));
		memset(p,0,sizeof(p));
		cnt=0;
	}

	bool ins(long long val){
		for (int i=62;i>=0;i--) {
			if (val&(1LL<<i)){
				if (!d[i]){
					d[i]=val;
					break;
				}
				val^=d[i];
			}
		}
		return val>0;
	}

	long long query_max(long long D=0LL){
		long long ret=D;
		for (int i=62;i>=0;i--)
			if ((ret^d[i])>ret) ret^=d[i];
		return ret;
	}

    long long query_min(long long D=0LL){
        long long ret=D;
        for(int i=0;i<=62;i++){
            if(d[i]) ret^=d[i];
        }
        return ret;
    }

	void rebuild(){
		for (int i=1;i<=62;i++)
			for (int j=0;j<i;j++)
				if (d[i]&(1LL<<j)) d[i]^=d[j];
		cnt=0;
		for (int i=0;i<=62;i++)
			if (d[i]) p[cnt++]=d[i];
	}
    //第K大
	long long kthquery(long long k){
		long long ret=0;
		if (k>=(1LL<<cnt)) return -1;
		for (int i=0;i<=62;i++)
			if (k&(1LL<<i)) ret^=p[i];
		return ret;
	}
	Linear_Basis merge(const Linear_Basis &n1,const Linear_Basis &n2){
	    Linear_Basis ret=n1;
	    for(int i=62;i>=0;i--)
            if(n2.d[i])ret.ins(n2.d[i]);
        return ret;
	}
};
struct node{
    int base[32];
    node(){for(int i=0;i<32;i++)base[i]=0;}
    void insert(int x){
        for(int i=31;~i;i--){
            if(x>>i&1){
                if(!base[i]){
                    base[i]=x;
                    return;
                }
                x^=base[i];
            }
        }
    }
    int check(int x) {
        for (int i = 31; ~i; i--)
        if (x >> i & 1) {
            if (!base[i]) {
                return 0;
            }
            x ^= base[i];
        }
        return 1;
    }
    node intersect(node a, node b) {///线性基求交
        node tmp, d, ans;
        for (int i = 0; i < 32; i++)
        if (a.base[i]) {
            tmp.base[i] = a.base[i];
            d.base[i] = 1 << i;
        }
        for (int i = 31; ~i; i--)
        if (b.base[i]) {
            int flag = 1, k = 0, v = b.base[i];
            for (int j = i; ~j; j--)
            if (v >> j & 1) {
                if (tmp.base[j]) {
                    v ^= tmp.base[j];
                    k ^= d.base[j];
                }
                else {
                    flag = 0;
                    tmp.base[j] = v;
                    d.base[j] = k;
                    break;
                }
            }
            if (flag) {
                int val = 0;
                for (int j = 31; ~j; j--)
                if (k >> j & 1)
                    val ^= a.base[j];
                ans.insert(val);
            }
        }
        return ans;
    }
}tree[maxn<<2];

几何

知识点

1
线段上的整点个数，(x1,y1)(x2,y2)两点连线之间的整点数是gcd(|x1−x2|,|y1−y2|)+1

弧度转换,点绕点旋转

欧拉定理：设平面图的顶点数，边数和面数分别为V,E,和F，则V+F-E=2

其中顺时针旋转为负，逆时针旋转为正，角度angle是弧度值，如旋转30度转换为弧度为： $angle = pi/180 * 30$。

4、度与角度的转换
根据圆为$360 º​$，弧度为$2π​$，即 $360º = 2π​$

4.1 角度转弧度：$2π / 360 = π / 180 ≈ 0.0174rad​$, 即: $度数 (π / 180） = 弧度​$
例如：将30º转为弧度rad
$ 30º (π / 180）= 0.523320 rad ​$

4.2 弧度转角度: $360 / 2π = 180 / π ≈ 57.3º​$, 即: $ 弧度 (180 / π） = 度数​$
例如：将$0.523320rad​$转为度º
$0.523320rad (180 / π) = 29.9992352688º ​$

若o不是原点，则可先将a点坐标转换为相对坐标计算，计算结果再加上o点坐标。

参与计算的a点坐标实际应为 a - 0,最终计算公式如下：

$b.x = ( a.x - o.x)cos(angle) - (a.y - o.y)sin(angle) + o.x$

$b.y = (a.x - o.x)sin(angle) + (a.y - o.y)cos(angle) + o.y$

刘汝佳套餐

Point

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
const double inf=1e200;
const double eps=1e-8;
const double pi=4*atan(1.0);
struct Point{
    double x,y;
    Point(double a=0,double b=0):x(a),y(b){}
    void input(){
        cin>>x>>y;
    }
};

typedef Point Vector;
int dcmp(double x){ return fabs(x)<eps?0:(x<0?-1:1);}
//向量+向量=向量，点+向量=点
Vector operator +(Vector A,Vector B){ return Vector(A.x+B.x,A.y+B.y);}
//点-点=向量
Vector operator -(Point A,Point B){ return Vector(A.x-B.x,A.y-B.y);}
//向量*数=向量
Vector operator *(Vector A,double p){ return Vector(A.x*p,A.y*p);}
//向量/数=向量
Vector operator /(Vector A,double p){ return Vector(A.x/p,A.y/p);}

bool operator<(const Point& a, const Point& b){
    return a.x < b.x || (a.x == b.x && a.y < b.y);
}
bool operator ==(const Point& a,const Point& b) {
    return dcmp(a.x-b.x)==0&&dcmp(a.y-b.y)==0;
}
double dot(Vector A,Vector B){ return A.x*B.x+A.y*B.y;}
double det(Vector A,Vector B){ return A.x*B.y-A.y*B.x;}
double dot(Point O,Point A,Point B){ return dot(A-O,B-O);}
double det(Point O,Point A,Point B){ return det(A-O,B-O);}
double length(Vector A){ return sqrt(dot(A,A));}
double angle(Vector A,Vector B){ return acos(dot(A,B)/length(A)/length(B));}
double area2(Point A,Point B,Point C){return det(B-A,C-A);}

//rad是弧度
Vector Rotate(Vector A,double rad)
{
    return Vector(A.x*cos(rad)-A.y*sin(rad),
                  A.x*sin(rad)+A.y*cos(rad));
}
//调用前请确保A不是零向量 单位法向量 左转90°长度归一
Vector normal(Vector A)
{
    double L = length(A);
    return Vector(-A.y / L, A.x / L);
}
//调用前保证两条直线P+tv和Q+tw有唯一交点。当且仅当Cross(v, w)非0->平行
Point jiaoPoint(Point p,Vector v,Point q,Vector w)
{   //p+tv q+tw，点加向量表示直线，求直线交点
    Vector u=p-q;
    double t=det(w,u)/det(v,w);
    return p+v*t;
}

double distoline(Point P,Point A,Point B)
{
    //点到直线距离
    Vector v1=B-A,v2=P-A;
    return fabs(det(v1,v2)/length(v1));//如果不取绝对值，得到的是有向距离
}
double distoseg(Point P,Point A,Point B)
{
    //点到线段距离 ///钝角<0,锐角>0,直角=0
    if(A==B) return length(P-A);
    Vector v1=B-A,v2=P-A,v3=P-B;
    if(dcmp(dot(v1,v2))<0) return length(v2);
    else if(dcmp(dot(v1,v3))>0) return length(v3);
    return fabs(det(v1,v2)/length(v1));
}
Point GetLineProjection(Point p,Point A,Point B){
    //点P到AB的投影
    Vector v=B - A;
    return A + v * (dot(v,p-A)/dot(v,v));
}
bool SegmentProperIntersection(Point a1,Point a2,Point b1,Point b2)   {
    //规范相交
    double c1=det(a2-a1,b1-a1),c2=det(a2-a1,b2-a1);
    double c3=det(b2-b1,a1-b1),c4=det(b2-b1,a2-b1);
    return dcmp(c1)*dcmp(c2)<0&&dcmp(c3)*dcmp(c4)<0; ///端点相交加上等于
    /*
    &&max(a1.x,a2.x)>=min(b1.x,b2.x)
    &&max(b1.x,b2.x)>=min(a1.x,a2.x)
    &&max(a1.y,a2.y)>=min(b1.y,b2.y)
    &&max(b1.y,b2.y)>=min(a1.y,a2.y);
    */
}
bool isPointOnSegment(Point p,Point a1,Point a2)
{
    //点是否在线段上
    return dcmp(det(a1-p,a2-p)==0)&&dcmp(dot(a1-p,a2-p)<0);
}

Circle

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177

struct Line
{
    Point p;    //直线上任意一点
    Vector v;   //方向向量。它的左边就是对应的半平面
    double ang; //极角。即从x正半轴旋转到向量v所需要的角（弧度）
    Line() {}
    Line(Point p, Vector v) : p(p), v(v) { ang = atan2(v.y, v.x); }
    bool operator<(const Line& L) const // 排序用的比较运算符
    {
        return ang < L.ang;
    }
    Point point(double t) { return p + v * t; }
};

struct Circle
{
    Point c;
    double r;
    Circle(Point c=Point(0,0), double r=0) : c(c), r(r) {}
    Point point(double a) { return Point(c.x + cos(a) * r, c.y + sin(a) * r); }
};

int getLineCircleIntersection(Line L, Circle C, double& t1, double& t2, vector<Point>& sol)
{
    double a = L.v.x, b = L.p.x - C.c.x, c = L.v.y, d = L.p.y - C.c.y;
    double e = a * a + c * c, f = 2 * (a * b + c * d), g = b * b + d * d - C.r * C.r;
    double delta = f * f - 4 * e * g; //判别式
    if (dcmp(delta) < 0) return 0;    //相离
    if (dcmp(delta) == 0)             //相切
    {
        t1 = t2 = -f / (2 * e);
        sol.push_back(L.point(t1));
        return 1;
    }
    //相交
    t1 = (-f - sqrt(delta)) / (2 * e);
    t2 = (-f + sqrt(delta)) / (2 * e);
    sol.push_back(L.point(t1));
    sol.push_back(L.point(t2));
    return 2;
}

double angle(Vector v) { return atan2(v.y, v.x); }

int getCircleCircleIntersection(Circle C1, Circle C2, vector<Point>& sol)
{
    double d = Length(C1.c - C2.c);
    if (dcmp(d) == 0)
    {
        if (dcmp(C1.r - C2.r) == 0) return -1; //两圆重合
        return 0;
    }
    if (dcmp(C1.r + C2.r - d) < 0) return 0;       //内含
    if (dcmp(fabs(C1.r - C2.r) - d) > 0) return 0; //外离

    double a = angle(C2.c - C1.c); //向量C1C2的极角
    double da = acos((C1.r * C1.r + d * d - C2.r * C2.r) / (2 * C1.r * d));
    //C1C2到C1P1的角
    Point p1 = C1.point(a - da), p2 = C1.point(a + da);
    sol.push_back(p1);
    if (p1 == p2) return 1;
    sol.push_back(p2);
    return 2;
}
//过点p到圆C的切线，v[i]是第i条切线的向量，返回切线条数
int getTangents(Point p, Circle C, Vector* v)
{
    Vector u = C.c - p;
    double dist = Length(u);
    if (dist < C.r)
        return 0;
    else if (dcmp(dist - C.r) == 0)
    { //p在圆上，只有一条切线
        v[0] = Rotate(u, pi / 2);
        return 1;
    }
    else
    {
        double ang = asin(C.r / dist);
        v[0] = Rotate(u, -ang);
        v[1] = Rotate(u, +ang);
        return 2;
    }
}

//两圆的公切线
//返回切线的条数。-1表示无穷条切线。
//a[i]和b[i]分别是第i条切线在圆A和圆B上的切点
int getTangents(Circle A, Circle B, Point* a, Point* b)
{
    int cnt = 0;
    if (A.r < B.r)
    {
        swap(A, B);
        swap(a, b);
    }
    int d2 = (A.c.x - B.c.x) * (A.c.x - B.c.x) + (A.c.y - B.c.y) * (A.c.y - B.c.y);
    int rdiff = A.r - B.r;
    int rsum = A.r + B.r;
    if (d2 < rdiff * rdiff) return 0; //内含
    double base = atan2(B.c.y - A.c.y, B.c.x - A.c.x);
    if (d2 == 0 && A.r == B.r) return -1; //无限多条切线
    if (d2 == rdiff * rdiff)
    { //内切，一条切线
        a[cnt] = A.point(base);
        b[cnt] = B.point(base);
        cnt++;
        return 1;
    }
    //有外共切线
    double ang = acos((A.r - B.r) / sqrt(d2));
    a[cnt] = A.point(base + ang);
    b[cnt] = B.point(base + ang);
    cnt++;
    a[cnt] = A.point(base + ang);
    b[cnt] = B.point(base - ang);
    cnt++;
    if (d2 == rsum * rsum)
    {
        a[cnt] = A.point(base);
        b[cnt] = B.point(pi + base);
        cnt++;
    }
    else if (d2 > rsum * rsum)
    {
        double ang = acos((A.r + B.r) / sqrt(d2));
        a[cnt] = A.point(base + ang);
        b[cnt] = B.point(pi + base + ang);
        cnt++;
        a[cnt] = A.point(base - ang);
        b[cnt] = B.point(pi + base - ang);
        cnt++;
    }
    return cnt;
}
//三角形外接圆（三点保证不共线）
Circle CircumscribedCircle(Point p1, Point p2, Point p3)
{
    double Bx = p2.x - p1.x, By = p2.y - p1.y;
    double Cx = p3.x - p1.x, Cy = p3.y - p1.y;
    double D = 2 * (Bx * Cy - By * Cx);
    double cx = (Cy * (Bx * Bx + By * By) - By * (Cx * Cx + Cy * Cy)) / D + p1.x;
    double cy = (Bx * (Cx * Cx + Cy * Cy) - Cx * (Bx * Bx + By * By)) / D + p1.y;
    Point p = Point(cx, cy);
    return Circle(p, Length(p1 - p));
}

//三角形内切圆
Circle InscribedCircle(Point p1, Point p2, Point p3)
{
    double a = Length(p2 - p3);
    double b = Length(p3 - p1);
    double c = Length(p1 - p2);
    Point p = (p1 * a + p2 * b + p3 * c) / (a + b + c);
    return Circle(p, distoline(p, p1, p2));
}
double ok(double x){
    while(x>=pi)x-=pi;
    while(x<0)x+=pi;
    return x;
}

//平行线.
void Parallel(Point A,Point B,double r,vector<Line> &sol){
    Vector AB=normal(B-A);
    AB=AB*r;
    Point AA=A+AB,BB=B+AB;
    Line L1=Line(AA,BB-AA);
    sol.push_back(L1);
    AA=A-AB,BB=B-AB;
    Line L2=Line(AA,BB-AA);
    sol.push_back(L2);
}
double torad(double deg){
    return deg/180*pi;
}

Polygon

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

typedef vector<Point> Polygon;
//多边形的有向面积
double PolygonArea(Polygon po)
{
    int n = po.size();
    double area = 0.0;
    for (int i = 1; i < n - 1; i++)
        area += det(po[i] - po[0], po[i + 1] - po[0]);
    return area / 2;
}

int isPointInPolygon(Point p,vector<Point>poly)
{
    //判断点与多边形的位置关系
    int wn=0,sz=poly.size();
    for(int i=0;i<sz;i++){
        if(isPointOnSegment(p,poly[i],poly[(i+1)%sz])) return -1; //边界上
        int k=dcmp(det(poly[(i+1)%sz]-poly[i],p-poly[i]));
        int d1=dcmp(poly[i].y-p.y);
        int d2=dcmp(poly[(i+1)%sz].y-p.y);
        if(k>0&&d1<=0&&d2>0) wn++;
        if(k<0&&d2<=0&&d1>0) wn--;
    }
    if(wn!=0) return 1;//内部
    return 0;          //外部
}
//凸包(Andrew算法)
//如果不希望在凸包的边上有输入点，把两个 <= 改成 <
//如果不介意点集被修改，可以改成传递引用
Polygon ConvexHull(vector<Point> p){
    sort(p.begin(),p.end());
    p.erase(unique(p.begin(),p.end()),p.end());
    int n=p.size(),m=0;
    Polygon res(n+1);
    for(int i=0;i<n;i++){
        while(m>1&&det(res[m-1]-res[m-2],p[i]-res[m-2])<=0)m--;
        res[m++]=p[i];
    }
    int k=m;
    for(int i=n-2;i>=0;i--){
        while(m>k&&det(res[m-1]-res[m-2],p[i]-res[m-2])<=0)m--;
        res[m++]=p[i];
    }
    m-=n>1;
    res.resize(m);
    return res;
}

付队模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
#define mp make_pair
typedef long long ll;
const double inf=1e200;
const double eps=1e-8;
const double pi=4*atan(1.0);
struct point{
    double x,y;
    point(double a=0,double b=0):x(a),y(b){}
};
int dcmp(double x){ return fabs(x)<eps?0:(x<0?-1:1);}
point operator +(point A,point B) { return point(A.x+B.x,A.y+B.y);}
point operator -(point A,point B) { return point(A.x-B.x,A.y-B.y);}
point operator *(point A,double p){ return point(A.x*p,A.y*p);}
point operator /(point A,double p){ return point(A.x/p,A.y/p);}
point rotate(point A,double rad){
    return point(A.x*cos(rad)-A.y*sin(rad), A.x*sin(rad)+A.y*cos(rad));
}
bool operator ==(const point& a,const point& b) {
     return dcmp(a.x-b.x)==0&&dcmp(a.y-b.y)==0;
}
double dot(point A,point B){ return A.x*B.x+A.y*B.y;}
double det(point A,point B){ return A.x*B.y-A.y*B.x;}
double dot(point O,point A,point B){ return dot(A-O,B-O);}
double det(point O,point A,point B){ return det(A-O,B-O);}
double length(point A){ return sqrt(dot(A,A));}
double angle(point A,point B){ return acos(dot(A,B)/length(A)/length(B));}
double distoline(point P,point A,point B)
{
    //点到直线距离
    point v1=B-A,v2=P-A;
    return fabs(det(v1,v2)/length(v1));
}
double distoseg(point P,point A,point B)
{
    //点到线段距离
    if(A==B) return length(P-A);
    point v1=B-A,v2=P-A,v3=P-B;
    if(dcmp(dot(v1,v2))<0) return length(v2);
    else if(dcmp(dot(v1,v3))>0) return length(v3);
    return fabs(det(v1,v2)/length(v1));
}
double Ployarea(vector<point>p)
{
    //多边形面积
    double ans=0; int sz=p.size();
    for(int i=1;i<sz-1;i++) ans+=det(p[i]-p[0],p[i+1]-p[0]);
    return ans/2.0;
}
bool SegmentProperIntersection(point a1,point a2,point b1,point b2)   {
    //规范相交
    double c1=det(a2-a1,b1-a1),c2=det(a2-a1,b2-a1);
    double c3=det(b2-b1,a1-b1),c4=det(b2-b1,a2-b1);
    return dcmp(c1)*dcmp(c2)<0&&dcmp(c3)*dcmp(c4)<0;
}
bool isPointOnSegment(point p,point a1,point a2)
{
    //点是否在线段上
    return dcmp(det(a1-p,a2-p)==0&&dcmp(dot(a1-p,a2-p))<0);
}
int isPointInPolygon(point p,vector<point>poly)
{
    //判断点与多边形的位置关系
    int wn=0,sz=poly.size();
    for(int i=0;i<sz;i++){
        //在边上
        if(isPointOnSegment(p,poly[i],poly[(i+1)%sz])) return -1;
        int k=dcmp(det(poly[(i+1)%sz]-poly[i],p-poly[i]));
        int d1=dcmp(poly[i].y-p.y); int d2=dcmp(poly[(i+1)%sz].y-p.y);
        if(k>0&&d1<=0&&d2>0) wn++;
        if(k<0&&d2<=0&&d1>0) wn--;
    }
    if(wn!=0) return 1;//内部
    return 0;          //外部
}
double seg(point O,point A,point B){
    if(dcmp(B.x-A.x)==0) return (O.y-A.y)/(B.y-A.y);
    return (O.x-A.x)/(B.x-A.x);
}
pair<double,int>s[110*60];
double polyunion(vector<point>*p,int N){ //有多个才加*,单个不加，有改变的加&
    //求多边形面积并
    double res=0;
    for(int i=0;i<N;i++){
        int sz=p[i].size();
        for(int j=0;j<sz;j++){
            int m=0;
            s[++m]=mp(0,0);
            s[++m]=mp(1,0);
            point a=p[i][j],b=p[i][(j+1)%sz];
            for(int k=0;k<N;k++){
                if(i!=k){
                    int sz2=p[k].size();
                    for(int ii=0;ii<sz2;ii++){
                        point c=p[k][ii],d=p[k][(ii+1)%sz2];
                        int c1=dcmp(det(b-a,c-a));
                        int c2=dcmp(det(b-a,d-a));
                        if(c1==0&&c2==0){
                            if(dcmp(dot(b-a,d-c))){
                                s[++m]=mp(seg(c,a,b),1);
                                s[++m]=mp(seg(c,a,b),-1);
                            }
                        }
                        else{
                            double s1=det(d-c,a-c);
                            double s2=det(d-c,b-c);
                            if(c1>=0&&c2<0) s[++m]=mp(s1/(s1-s2),1);
                            else if(c1<0&&c2>=0) s[++m]=mp(s1/(s1-s2),-1);
                        }
                    }
                }
            }
            sort(s+1,s+m+1);
            double pre=min(max(s[1].first,0.0),1.0),now,sum=0;
            int cov=s[0].second;
            for(int j=2;j<=m;j++){
                now=min(max(s[j].first,0.0),1.0);
                if(!cov) sum+=now-pre;
                cov+=s[j].second;
                pre=now;
            }
            res+=det(a,b)*sum;
        }
    }
    return -(res/2);
}
point jiaopoint(point p,point v,point q,point w)
{   //p+tv q+tw，点加向量表示直线，求直线交点
    point u=p-q;
    double t=det(w,u)/det(v,w);
    return p+v*t;
}
point GetCirPoint(point a,point b,point c)
{
    point p=(a+b)/2;    //ad中点
    point q=(a+c)/2;    //ac中点
    point v=rotate(b-a,pi/2.0),w=rotate(c-a,pi/2.0);   //中垂线的方向向量
    if (dcmp(length(det(v,w)))==0)    //平行
    {
        if(dcmp(length(a-b)+length(b-c)-length(a-c))==0) return (a+c)/2;
        if(dcmp(length(b-a)+length(a-c)-length(b-c))==0) return (b+c)/2;
        if(dcmp(length(a-c)+length(c-b)-length(a-b))==0) return (a+b)/2;
    }
    return jiaopoint(p,v,q,w);
}
point MinCircular(point *P,int n)
{
    //最小圆覆盖 ,看起来是O(N^3)，期望复杂度为O(N)
    random_shuffle(P+1,P+n+1);    //随机化
    point c=P[1]; double r=0;   //c 圆心,,//r 半径
    for (int i=2;i<=n;i++)
        if (dcmp(length(c-P[i])-r)>0)    //不在圆内
        {
            c=P[i],r=0;
            for (int j=1;j<i;j++)
                if (dcmp(length(c-P[j])-r)>0)
                {
                    c=(P[i]+P[j])/2.0;
                    r=length(c-P[i]);
                    for (int k=1;k<j;k++)
                        if (dcmp(length(c-P[k])-r)>0)
                        {
                            c=GetCirPoint(P[i],P[j],P[k]);
                            r=length(c-P[i]);
                        }
                }
        }
    //cout<<r<<":"<<c.x<<" "<<c.y<<endl;
    return c;
}
const int maxn=400010;
bool cmp(point a,point b){ return a.x==b.x?a.y<b.y:a.x<b.x; }
point f[maxn],c[maxn],ch[maxn];
void convexhull(point *a,int n,int &top)
{
    //水平序的Andrew算法求凸包。
    sort(a+1,a+n+1,cmp); top=0;
    for(int i=1;i<=n;i++){ //求下凸包
        while(top>=2&&det(ch[top-1],ch[top],a[i])<=0) top--;
        ch[++top]=a[i];
    }
    int ttop=top;
    for(int i=n-1;i>=1;i--){ //求上凸包
        while(top>ttop&&det(ch[top-1],ch[top],a[i])<=0) top--;
        ch[++top]=a[i];
    }
}
void P(double x)
{
    //if(fabs(x)<0.000001) puts("0.00000000"); else
    printf("%.9lf",x);
}

球体积交

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
#include <bits/stdc++.h>
using namespace std;
 
const int maxn = 1e2 + 5;
const double pi = acos(-1.0);
const double eps = 1e-8;
 
int Sgn(double X) {
    if (fabs(X) < eps) {
        return 0;
    }
    return X < 0 ? -1 : 1;
}
 
struct Point {
    double X, Y, Z;
 
    void Input() {
        scanf("%lf%lf%lf", &X, &Y, &Z);
    }
};
 
typedef Point Vector;
 
Vector operator + (Vector Key1, Vector Key2) {
    return (Vector){Key1.X + Key2.X, Key1.Y + Key2.Y, Key1.Z + Key2.Z};
}
 
Vector operator - (Vector Key1, Vector Key2) {
    return (Vector){Key1.X - Key2.X, Key1.Y - Key2.Y, Key1.Z - Key2.Z};
}
 
double operator * (Vector Key1, Vector Key2) {
    return Key1.X * Key2.X + Key1.Y * Key2.Y + Key1.Z * Key2.Z;
}
 
double Length(Vector Key) {
    return sqrt(Key * Key);
}
 
double operator ^ (Vector Key1, Vector Key2) {
    return Length((Vector){Key1.Y * Key2.Z - Key1.Z * Key2.Y, Key1.Z * Key2.X - Key1.X * Key2.Z, Key1.X * Key2.Y - Key1.Y * Key2.X});
}
 
double DisPointToPoint(Point Key1, Point Key2) {
    return sqrt((Key1 - Key2) * (Key1 - Key2));
}
 
struct Sphere {
    double pi=acos(-1.0);
    Point Center;
    double Radius;
 
    void Input() {
        Center.Input();
        scanf("%lf", &Radius);
    }
    double get(){
        return (4.0/3.0)*pi*Radius*Radius*Radius;
    }
};
 
double CalVolume(Sphere Key) {
    return 4.0 / 3.0 * pi * Key.Radius * Key.Radius * Key.Radius;
}
 
double SphereIntersectVolume(Sphere Key1, Sphere Key2) {
    double Ans = 0.0;
    double Dis = DisPointToPoint(Key1.Center, Key2.Center);
    if (Sgn(Dis - Key1.Radius - Key2.Radius) >= 0) {
        return Ans;
    }
    if (Sgn(Key2.Radius - (Dis + Key1.Radius)) >= 0) {
        return CalVolume(Key1);
    }
    else if (Sgn(Key1.Radius - (Dis + Key2.Radius)) >= 0) {
        return CalVolume(Key2);
    }
    double Length1 = ((Key1.Radius * Key1.Radius - Key2.Radius * Key2.Radius) / Dis + Dis) / 2;
    double Length2 = Dis - Length1;
    double X1 = Key1.Radius - Length1, X2 = Key2.Radius - Length2;
    double V1 = pi * X1 * X1 * (Key1.Radius - X1 / 3.0);
    double V2 = pi * X2 * X2 * (Key2.Radius - X2 / 3.0);
    return V1 + V2;
}
 
int T;
int N;
Sphere a;
Sphere b;
double ans;
 
int main(int argc, char *argv[]) {
 
    a.Input();
    b.Input();
    ans=a.get()+b.get()-SphereIntersectVolume(a,b);
    cout<<fixed<<setprecision(15);
    cout<<ans<<endl;
    return 0;
}

其他

分块

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
    int n;
    cin>>n;
    block=sqrt(n);
    for(int i=1;i<=n;i++){
        in[i]=(i-1)/block+1;
        cin>>a[i];
        s[in[i]]+=a[i];
    }
ll query(int l,int r){
    ll ans=0;
    if(in[l]==in[r]){
        for(int i=l;i<=r;i++)ans+=a[i];
        return ans;
    }
    for(int i=l;in[i]==in[l];i++)ans+=a[i];
    for(int i=r;in[i]==in[r];i--)ans+=a[i];
    for(int i=in[l]+1;i<in[r];i++)ans+=(s[i]);
    return ans;
}
block*(i-1)+1 ///块i的第一个位置
///查询区间小于一个数的个数   二分
///查询区间某数前驱， 		二分
///在某个位置插入一个数（vector 暴力插入 后定期重构（块大小大于原块的五倍。
v[i].insert( v[i].begin() + wh - 1, x );//插入~ ///在这个块的第wh个位置插入值为x的数。

分块的一些技巧

查询区间一个数的个数 （二分

查询区间某数前驱 （二分

在某个位置插入一个数（vector 暴力插入 后定期重构（块大小大于原块的五倍。

bitset

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
对于一个叫做bit的bitset：
bit.size()       返回大小（位数）
bit.count()     返回1的个数
bit.any()       返回是否有1
bit.none()      返回是否没有1
bit.set()       全都变成1
bit.set(p)      将第p + 1位变成1（bitset是从第0位开始的！） 
bit.set(p, x)   将第p + 1位变成x
bit.reset()     全都变成0
bit.reset(p)    将第p + 1位变成0
bit.flip()      全都取反
bit.flip(p)     将第p + 1位取反
bit.to_ulong()  返回它转换为unsigned long的结果，如果超出范围则报错
bit.to_ullong() 返回它转换为unsigned long long的结果，如果超出范围则报错
bit.to_string() 返回它转换为string的结果

斜率DP

画图判断交点的位置决定是否剔除

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
$dp[i][j]=dp[k][j-1]+(sum[i]-sum[k])-h[k+1]*(w[i]-w[k])$

const int maxn=5500+50;

int n,k;
struct node{
    ll h,w;
    bool operator< (const node &o)const{
        return h<o.h;
    }
}my[maxn];
ll dp[5050][5050]; ///前i个木块 做J个

int q[maxn];
int head,tail;
__int128 sum[maxn];
__int128 h[maxn];
__int128 w[maxn];
__int128 getDP(int i,int k,int id){  ///dp[i][id]= dp[i][k]+sum[k+1][i];
    return dp[k][id-1]+(sum[i]-sum[k])-__int128(h[k+1]*(w[i]-w[k]));
}
__int128 getUP(int y,int x,int id){ /// y<x 且x更优秀
    return dp[x][id-1]-dp[y][id-1]+sum[y]-sum[x]-__int128(h[y+1]*w[y])+__int128(h[x+1]*w[x]);
}
__int128 getDOWN(int y,int x,int i){
    return h[x+1]-h[y+1];
}

int main()
{
    std::ios::sync_with_stdio(false);
    cin>>n>>k;
    for(int i=1;i<=n;i++)cin>>my[i].w>>my[i].h;
    sort(my+1,my+1+n);
    for(int i=1;i<=n;i++){
        w[i]=w[i-1]+my[i].w;
        sum[i]=sum[i-1]+1LL*my[i].w*my[i].h;
        h[i]=my[i].h;
    }
    for(int i=1;i<=n;i++)dp[i][1]=sum[i]-sum[0]-h[1]*(w[i]-w[0]);

    for(int j=2;j<=k;j++){
        head=tail=0;
        q[++tail]=j-1;
        for(int i=j;i<=n;i++){
            while(head+2<=tail&&getUP(q[head+1],q[head+2],j)<=getDOWN(q[head+1],q[head+2],j)*w[i])
                head++;
            dp[i][j]=getDP(i,q[head+1],j);
            while(head+2<=tail&&__int128(getUP(q[tail-1],q[tail],j)*getDOWN(i,q[tail],j))<=__int128(getUP(i,q[tail],j)*getDOWN(q[tail-1],q[tail],j)))
     // 取min用<= 取max 用>=
                
     //根据x是递增还是递减 加上取min还是取max 决定大于小于
                
      //min + 递增 下凸包 <=
      //min + 递减 上凸包 >=
      //max + 递增 上凸包 >=
      //max + 递减 下凸包 <=
                tail--;
            q[++tail]=i;
        }
    }
    cout<<dp[n][k]<<endl;
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
///
const int maxn=4e6+50;
struct node{
    ll h,w;
    bool operator<(const node &o)const{
        if(h==o.h)return w>o.w;
        else return h>o.h;
    }
}a[maxn];

ll dp[maxn];
int q[maxn];
int head,tail;
ll getDP(int x,int i){
    return dp[x]+a[x+1].h*a[i].w;
}
ll getB(int x,int y){ ///1 2
    return dp[x]-dp[y];
}
ll getK(int x,int y){
    return a[y+1].h-a[x+1].h;
}
int main()
{
    std::ios::sync_with_stdio(false);
    int n;
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a[i].h>>a[i].w;
    }
    sort(a+1,a+1+n);
    int mi=0;
    int cnt=0;
    for(int i=1;i<=n;i++){
        if(a[i].w>mi){
            a[++cnt]=a[i];mi=a[i].w;
        }
    }
    n=cnt;
    //dp[1]=a[1].w*a[1].h;
    head=tail=0;
    q[++tail]=0;
    for(int i=1;i<=n;i++){
        while(head+2<=tail&&getDP(q[head+2],i)<=getDP(q[head+1],i))
            head++;
       // cout<<"q["<<head+1<<"]="<<q[head+1]<<endl;
        dp[i]=getDP(q[head+1],i);
        while(head+2<=tail&&getB(q[tail-1],q[tail])*getK(q[tail],i)>=getB(q[tail],i)*getK(q[tail-1],q[tail]))
            tail--;
        q[++tail]=i;
       // cout<<"dp["<<i<<"]="<<dp[i]<<endl;
    }
    cout<<dp[n]<<endl;
    return 0;
}

博弈

威佐夫博弈

1
2
3
4
5
6
7
scanf("%lld%lld",&a,&b);
   if(a>b) swap(a,b);
   int temp=abs(a-b);
   int ans=temp*(1.0+sqrt(5.0))/2.0;
   if(ans==a) printf("0");//先手必败
   else       printf("1");
   return 0;

sg函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int sg[maxn];
int vis[1500];
int getSG(int x){
    sg[0]=0;
    for(int i=1;i<=x;i++){
        memset(vis,0,sizeof(vis));
        for(int j=1;fib[j]<=i;j++)
            vis[sg[i-fib[j]]]=1;
        for(int j=0;j<=x;j++){
            if(vis[j]==0){
                sg[i]=j;break;
            }
        }
    }
}

ST表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int d[maxn][20],a[maxn],n;
int lg[maxn];
void init(){
    for(int i=1;i<=n;i++)d[i][0]=i;
    for(int j=1;(1<<j)<=n;j++){
        for(int i=1;i+(1<<j)-1<=n;i++){
            d[i][j]=(a[d[i][j-1]]>=a[d[i+(1<<(j-1))][j-1]])?
            d[i][j-1]:d[i+(1<<(j-1))][j-1];
        }
    }
}
    lg[0]=-1;
    for(int i=1;i<maxn;i++)lg[i]=lg[i>>1]+1;
	int k=lg[R-L+1];
    if(a[d[R-(1<<k)+1][k]]>a[d[L][k]])
        mid=d[R-(1<<k)+1][k];

枚举子集

1
for(int j=x;j;j=(j-1)&x) //枚举所有x的二进制子集

SOSDP

1
2
3
4
5
6
7
8
9
10
11
12
for(int i=0;i<4;i++){   ///n*logn 遍历所有子集
    for(int j=0;j<(1<<4);j++){
        if((j&(1<<i))==0){
            bitset<4> a(j);
            cout<<"i="<<i<<" pre="<<a<<" nex=";
            a.set(i);
            cout<<a.set(i)<<endl;
            v[j|(1<<i)].push_back(j);
            dp[j|(1<<i)]=max(dp[j|(1<<i)],dp[j]);
        }
    }
}

Prufer序列

理论

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
一棵n个节点的无根树唯一地对应了一个长度为n-2的数列，数列中的每个数都在1到n的范围内。

上面这句话比较重要。通过上面的定理，

1）我们可以直接推出n个点的无向完全图的生成树的计数：n^(n-2)   即n个点的有标号无根树的计数。

 

2）一个有趣的推广是，n个节点的度依次为D1, D2, …, Dn的无根树共有   (n-2)! / [ (D1-1)!(D2-1)!..(Dn-1)! ]  个，因为此时Prüfer编码中的数字i恰好出现Di-1次。

即 n种元素，共n-2个，其中第i种元素有Di-1个，求排列数。

 

3）n个节点的度依次为D1, D2, …, Dn，令有m个节点度数未知，求有多少种生成树？(BZOJ1005 明明的烦恼)

令每个已知度数的节点的度数为di，有n个节点，m个节点未知度数，left=(n-2)-(d1-1)-(d2-1)-...-(dk-1)

已知度数的节点可能的组合方式如下

(n-2)!/(d1-1)!/(d2-1)!/.../(dk-1)!/left!

剩余left个位置由未知度数的节点随意填补，方案数为m^left

于是最后有

ans=(n-2)!/(d1-1)!/(d2-1)!/.../(dk-1)!/left! * m^left

n个点的 有标号有根树的计数：n^(n-2)*n = n^(n-1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
prufer数列是一种无根树的编码表示，类似于hash。

一棵n个节点带编号的无根树，对应唯一串长度为n-2的prufer编码。所以一个n阶完全图的生成树个数就是n^(n-2)

首先定义无根树中度数为1的节点是叶子节点。

找到编号最小的叶子并删除，序列中添加与之相连的节点编号，重复执行直到只剩下2个节点。
	for (int i = 1; i <= n; i++) {
		if (degree[i] == 1) {
			gg.insert (i);
			vis[i] = 1;
		}
	}
 
	set<int>::iterator it;
	int prufer[maxn], id = 0;
	for (; id <= n-3;) {
		int u = (*(it = gg.begin ()));
		gg.erase (u);
		for (int i = head[u]; i != -1; i = edge[i].next) {
			int v = edge[i].v;
			if (vis[v])
				continue;
			degree[v]--;
			prufer[++id] = v;
			if (degree[v] == 1) {
				gg.insert (v);
				vis[v] = 1;
			}
		}
	}
	for (int i = 1; i <= id; i++) {
		cout << prufer[i] << " ";
	} cout << endl;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
（2）prufer序列转化为无根树。
设点集V={1,2,3,...,n}，每次取出prufer序列中最前面的元素u，在V中找到编号最小的没有在prufer序列中出现的元素v，给u，v连边然后分别删除，最后在V中剩下两个节点，给它们连边。最终得到的就是无根树。

具体实现也可以用一个set，维护prufer序列中没有出现的编号。复杂度O(nlgn)。

int n;
int prufer[maxn], node[maxn], cnt;
set<int> gg; //在prufer序列里没有出现的点
int vis[maxn]; //这个点是不是在prufer序列里面
bool used[maxn]; //这个点有没有使用过

	gg.clear ();
	memset (vis, 0, sizeof vis);
	memset (used, 0, sizeof used);
	cnt = 0;
	for (int i = 1; i <= n-2; i++) {
		cin >> prufer[i];
		vis[prufer[i]]++;
	}
	for (int i = 1; i <= n; i++) {
		if (!vis[i]) {
			gg.insert (i);
		}
	}
	set<int>::iterator it;
	for (int i = 1; i <= n-2; i++) {
		int v = (*(it = gg.begin ())), u = prufer[i];
		cout << u << "-" << v << endl;
		used[v] = 1;
		gg.erase (v);
		vis[u]--;
		if (!vis[u] && !used[u]) {
			gg.insert (u);
		}
	}
	it = gg.begin ();
	cout << *it << "-" << *(++it) << endl;

最后有一个很重要的性质就是prufer序列中某个编号出现的次数+1就等于这个编号的节点在无根树中的度数。

技巧

JAVA

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
import java.math.BigDecimal;
import java.math.BigInteger;
import java.util.Scanner;

        Scanner cin=new Scanner(System.in);

        BigInteger num1=new BigInteger("12345");
        BigInteger num2=cin.nextBigInteger();

        BigDecimal num3=new BigDecimal("123.45");
        BigDecimal num4=cin.nextBigDecimal();
import java.math.BigInteger;

public class Main {
    public static void main(String[] args) {
        BigInteger num1=new BigInteger("12345");
        BigInteger num2=new BigInteger("45");
        //加法
        System.out.println(num1.add(num2));
        //减法
        System.out.println(num1.subtract(num2));
        //乘法
        System.out.println(num1.multiply(num2));
        //除法(相除取整)
        System.out.println(num1.divide(num2));
        //取余
        System.out.println(num1.mod(num2));
        //最大公约数GCD
        System.out.println(num1.gcd(num2));
        //取绝对值
        System.out.println(num1.abs());
        //取反
        System.out.println(num1.negate());
        //取最大值
        System.out.println(num1.max(num2));
        //取最小值
        System.out.println(num1.min(num2));
        //是否相等
        System.out.println(num1.equals(num2));
    }
}
import java.math.BigDecimal;

public class Main {
    public static void main(String[] args) {
        BigDecimal num1=new BigDecimal("123.45");
        BigDecimal num2=new BigDecimal("4.5");
        //加法
        System.out.println(num1.add(num2));
        //减法
        System.out.println(num1.subtract(num2));
        //乘法
        System.out.println(num1.multiply(num2));
        //除法（在divide的时候就设置好要精确的小数位数和舍入模式）
        System.out.println(num1.divide(num2,10,BigDecimal.ROUND_HALF_DOWN));
        //取绝对值
        System.out.println(num1.abs());
        //取反
        System.out.println(num1.negate());
        //取最大值
        System.out.println(num1.max(num2));
        //取最小值
        System.out.println(num1.min(num2));
        //是否相等
        System.out.println(num1.equals(num2));
        //判断大小( > 返回1, < 返回-1)
        System.out.println(num2.compareTo(num1));
    }
}
while(cin.hasNext())//相当于EOF
二分求开根号
static BigInteger cal(BigInteger x){
        BigInteger l = BigInteger.ONE ;
        BigInteger r = x ;
        BigInteger temp = BigInteger.ZERO ;
        while(!l.equals(r)){
            BigInteger mid = (l.add(r)).divide(BigInteger.valueOf(2)) ;
            if(temp.compareTo(BigInteger.ZERO)!=0&&temp.compareTo(mid)==0){
                break ;
            }else{
                temp = mid ;
            }
            if(temp.compareTo(BigInteger.ZERO)==0){
                temp = mid ;
            }
            if(mid.multiply(mid).compareTo(x)==1){
                r=mid ;
            }else{
                l=mid ;
            }
        }
        if(l.multiply(l).compareTo(x)==1){
            l=l.subtract(BigInteger.ONE) ;
        }
        return l;
        
}
牛顿迭代求平方根
      static BigInteger cal(BigInteger x) {
          BigInteger ans=BigInteger.valueOf(0);
          if(x.equals(BigInteger.valueOf(0))==true)return ans;
          BigInteger r=BigInteger.valueOf(1);
          BigInteger l=BigInteger.valueOf(-1);
          while(true) {
              BigInteger nxt =r.add(x.divide(r)).shiftRight(1);
              if(nxt.equals(l)==true) {
                  if(l.compareTo(r)==-1)return r;
                  else return l;
              }
              l=r;r=nxt;
          }

      }

文件读入

1
2
freopen("input.txt","r",stdin);
freopen("output.txt","w",stdout);

扩栈

1
2
// 解决爆栈问题
#pragma comment(linker, "/STACK:1024000000,1024000000")

快速读入

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// 适用于正负整数
template <class T>
inline bool scan_d(T &ret)
{
    char c;
    int sgn;
    if (c = getchar(), c == EOF) return 0; //EOF
    while (c != '-' && (c < '0' || c > '9')) c = getchar();
    sgn = (c == '-') ? -1 : 1;
    ret = (c == '-') ? 0 : (c - '0');
    while (c = getchar(), c >= '0' && c <= '9') ret = ret * 10 + (c - '0');
    ret *= sgn;
    return 1;
}
inline void out(int x)
{
    if (x > 9) out(x / 10);
    putchar(x % 10 + '0');
}

莫队算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// ---
// 莫队算法,可以解决一类静态,离线区间查询问题。分成 $\sqrt{x}$ 块,分块排序。
// ---
struct query { int L, R, id; };
void solve(query node[], int m)
{
    memset(ans, 0, sizeof(ans));
    sort(node, node + m, [](query a, query b) {
        return a.l / unit < b.l / unit
               || a.l / unit == b.l / unit && a.r < b.r;
    });
    int L = 1, R = 0;
    for (int i = 0; i < m; i++)
    {
        while (node[i].L < L) add(a[--L]);
        while (node[i].L > L) del(a[L++]);
        while (node[i].R < R) del(a[R--]);
        while (node[i].R > R) add(a[++R]);
        ans[node[i].id] = tmp;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
//带修莫队，复杂度n^{5/3}
struct query{
    int id,l,r,x;
}Q[maxn];
struct update{
    int pos,val,rval;
}C[maxn];
void ac(){
    unit=pow(n,2.0/3.0);
    sort(Q+1,Q+1+q1,[](query a,query b){
        if(a.l/unit!=b.l/unit)return a.l/unit<b.l/unit;
        if(a.r/unit!=b.r/unit)return b.r/unit<b.r/unit;
        return a.x<b.x;
    });
    int L=1,R=0,X=0;
    for(int i=1;i<=q1;i++){
        while(Q[i].l>L)del(a[L++]);
        while(Q[i].l<L)add(a[--L]);
        while(Q[i].r>R)add(a[++R]);
        while(Q[i].r<R)del(a[R--]);
        while(Q[i].x<X)remove(i,X--);
        while(Q[i].x>X)insert(i,++X);
        ans[Q[i].id]=p;
    }
}

cdq分治

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
///矩形区间加 区间求和
struct node{
    int x1,y1,op,id;
}Q[maxn],q[maxn];ll c[MV];
int lowbit(int x){return x&(-x);}
void add(int x,int v){
    for(;x<MV;x+=lowbit(x))c[x]+=v;
}
ll sum(int x){
    ll ans=0;for(;x;x-=lowbit(x))ans+=c[x];return ans;
}
void cdq(int l,int r){
    if(l==r)return;int mid=(l+r)>>1;
    int lq=l,rq=mid+1,cnt1=0;
    cdq(l,mid);cdq(mid+1,r);
    while(lq<=mid&&rq<=r){
        if(Q[lq].x1<=Q[rq].x1){
            if(Q[lq].op==1)add(Q[lq].y1,Q[lq].id);
            q[++cnt1]=Q[lq];lq++;
        }
        else{
            if(Q[rq].op==2){
                ans[Q[rq].id]+=sum(Q[rq].y1);
            }
            else if(Q[rq].op==3){
                ans[Q[rq].id]-=sum(Q[rq].y1);
            }
            q[++cnt1]=Q[rq];rq++;
        }
    }
    while(rq<=r){
        if(Q[rq].op==2){
            ans[Q[rq].id]+=sum(Q[rq].y1);
        }
        else if(Q[rq].op==3){
            ans[Q[rq].id]-=sum(Q[rq].y1);
        }
        q[++cnt1]=Q[rq];rq++;
    }
    while(lq<=mid){
        if(Q[lq].op==1)add(Q[lq].y1,Q[lq].id);
        q[++cnt1]=Q[lq];lq++;
    }
    for(int i=l;i<=mid;i++)if(Q[i].op==1)add(Q[i].y1,-Q[i].id);
    for(int i=1;i<=cnt1;i++){
        Q[i+l-1]=q[i];
    }
}
int main()
{
    cin>>s>>w;
    while(true){
        cin>>op;
        if(op==1){
            int x,y,a;
            cin>>x>>y>>a;x++;y++;
            Q[++cnt]={x,y,1,a};
        }
        else if(op==2){
            int x1,y1,x2,y2;
            cin>>x1>>y1>>x2>>y2;x1++;y1++;x2++;y2++;
            Q[++cnt]={x1-1,y1-1,2,++m};
            Q[++cnt]={x2,y2,2,m};
            Q[++cnt]={x1-1,y2,3,m};
            Q[++cnt]={x2,y1-1,3,m};
        }
        else break;
    }
    cdq(1,cnt);

整体二分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
///带修查区间第K大
#include<iostream>
typedef long long ll;
using namespace std;
const ll inf=1e18;
const int maxn=2e5+10;
const ll mod=1e9+7;
//#define endl '\n'
int a[maxn],cnt,tot,n,m;;
int ans[maxn],c[maxn];
struct Q{
    int l,r,k,id,op;
}q[maxn*3],q2[maxn*3],q1[maxn*3];
int lowbit(int x){return x&(-x);}
void add(int x,int v){
    for(;x<=n;x+=lowbit(x))c[x]+=v;
}
int sum(int x){
    int ans=0;
    for(;x;x-=lowbit(x))ans+=c[x];return ans;
}
void solve(int l,int r,int ql,int qr){
    if(ql>qr)return;
    if(l==r){
        for(int i=ql;i<=qr;i++){
            if(q[i].op==2)ans[q[i].id]=l;
        }
        return;
    }
    int mid=(l+r)>>1,cnt1=0,cnt2=0,x;
    for(int i=ql;i<=qr;i++){
        if(q[i].op==1){
            if(q[i].l<=mid)q1[++cnt1]=q[i],add(q[i].id,q[i].r);
            else q2[++cnt2]=q[i];
        }
        else{
            x=sum(q[i].r)-sum(q[i].l-1);
            if(q[i].k<=x)q1[++cnt1]=q[i];
            else q[i].k-=x,q2[++cnt2]=q[i];
        }
    }
    for(int i=1;i<=cnt1;i++)
        if(q1[i].op==1)add(q1[i].id,-q1[i].r);
    for(int i=1;i<=cnt1;i++)q[ql+i-1]=q1[i];
    for(int i=1;i<=cnt2;i++)q[ql+i+cnt1-1]=q2[i];
    solve(l,mid,ql,ql+cnt1-1);
    solve(mid+1,r,ql+cnt1,qr);
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);std::cout.tie(0);
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>a[i],q[++cnt]={a[i],1,0,i,1};
    for(int i=1;i<=m;i++){
        char op;cin>>op;
        if(op=='Q'){
            int l,r,k;cin>>l>>r>>k;q[++cnt]={l,r,k,++tot,2};
        }
        else{
            int x,t;cin>>x>>t;
            q[++cnt]={a[x],-1,0,x,1};q[++cnt]={a[x]=t,1,0,x,1};
        }
    }
    solve(-1e9,1e9,1,cnt);
    for(int i=1;i<=tot;i++)cout<<ans[i]<<endl;
    return 0;
}

高精度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
// 加法 乘法 小于号 输出
struct bint
{
    int l;
    short int w[100000];
    bint(ll x = 0)
    {
        l = x == 0, memset(w, 0,sizeof(w));
        while (x) w[l++] = x % 10, x /= 10;
    }
    bool operator<(const bint& x) const
    {
        if (l != x.l) return l < x.l;
        int i = l - 1;
        while (i >= 0 && w[i] == x.w[i]) i--;
        return (i >= 0 && w[i] < x.w[i]);
    }
    bint operator+(const bint& x) const
    {
        bint ans;
        ans.l = l > x.l ? l : x.l;
        for (int i = 0; i < ans.l; i++)
        {
            ans.w[i] += w[i] + x.w[i];
            ans.w[i + 1] += ans.w[i] / 10;
            ans.w[i] = ans.w[i] % 10;
        }
        if (ans.w[ans.l] != 0) ans.l++;
        return ans;
    }
    bint operator*(const bint& x) const
    {
        bint res;
        int up, tmp;
        for (int i = 0; i < l; i++)
        {
            up = 0;
            for (int j = 0; j < x.l; j++)
            {
                tmp = w[i] * x.w[j] + res.w[i + j] + up;
                res.w[i + j] = tmp % 10;
                up = tmp / 10;
            }
            if (up != 0) res.w[i + x.l] = up;
        }
        res.l = l + x.l;
        while (res.w[res.l - 1] == 0 && res.l > 1) res.l--;
        return res;
    }
    void print()
    {
        for (int i = l - 1; ~i; i--) printf("%d", w[i]);
        puts("");
    }
};

矩阵

矩阵快速幂

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
typedef vector<ll>vec;
typedef vector<vec>mat;
mat mul(mat& A,mat &B){
    mat C(A.size(),vec(B[0].size()));
    for(int i=0;i<A.size();i++)
        for(int k=0;k<B.size();k++)
        if(A[i][k])
            for(int j=0;j<B[0].size();j++)
            C[i][j]=(C[i][j]+A[i][k]*B[k][j]%mod+mod)%mod;
    return C;
}
mat Pow(mat A,ll n){
    mat B(A.size(),vec(A.size()));
    for(int i=0;i<A.size();i++)B[i][i]=1;
    for(;n;n>>=1,A=mul(A,A))
        if(n&1)B=mul(B,A);
    return B;
}

高斯消元

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
void gauss()
{
    int now = 1, to;
    double t;
    for (int i = 1; i <= n; i++, now++)
    {
        /*for (to = now; !a[to][i] && to <= n; to++);
        //做除法时减小误差，可不写
        if (to != now)
            for (int j = 1; j <= n + 1; j++)
                swap(a[to][j], a[now][j]);*/
        t = a[now][i];
        for (int j = 1; j <= n + 1; j++) a[now][j] /= t;
        for (int j = 1; j <= n; j++)
            if (j != now)
            {
                t = a[j][i];
                for (int k = 1; k <= n + 1; k++) a[j][k] -= t * a[now][k];
            }
    }
}
int gauss(int n,int m){
   int col, i, mxr, j, row;
   for (row = col = 1; row <= n && col <= m;row++,col++){
      mxr = row;
      for (i = row + 1; i <= n;i++)
      if(fabs(a[i][col])>fabs(a[mxr][col]))
         mxr = i;
      if(mxr!=row)
         swap(a[row], a[mxr]);
      if(fabs(a[row][col])<eps){
         row--;
         continue;
      }
      for (i = 1; i <= n;i++) /////消成上三角矩阵
         if(i!=row&&fabs(a[i][col])>eps)
            for (j = m; j >= col;j--)
               a[i][j] -= a[row][j] / a[row][col] * a[i][col];
         
   }
   row--;
   for (i = row; i >= 1;i--){//////回代成对角矩阵
      for (j = i + 1; j <= row;j++){
         a[i][m] -= a[j][m] * a[i][j];
      }
      a[i][m] /= a[i][i];
   }
   return row;
}

数位DP

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int num[20];
int dp[20][2];
int dfs(int pos,int pre,int sta,bool first){
    if(pos==-1)return 1;
    if(!first&&dp[pos][sta]!=-1)return dp[pos][sta];
    int up=first?num[pos]:9;
    int ans=0;
    for(int i=0;i<=up;i++){
        if(pre==6&&i==2)continue;
        if(i==4)continue;
        ans+=dfs(pos-1,i,i==6,first&&i==num[pos]);
    }
    if(!first)dp[pos][sta]=ans;
    return ans;
}
int ac(int x){
    int pos=0;
    while(x){
        num[pos++]=x%10;
        x/=10;
    }
    return dfs(pos-1,-1,0,true);
}