(寒假开黑gym)2017-2018 ACM-ICPC German Collegiate Programming Contest (GCPC 2017)

Diposting di | Edited on

传送门

付队！

许老师！

B.Buildings （polya定理）

题意

B：给你m面墙，每面墙是n*n的格子，你有c种颜色，问你有多少种涂色方案。用polya定理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=3e5+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
///a<mod 并且 p为素数
ll pow_mod(ll x, ll n, ll mod){
    ll res=1;
    while(n){
        if(n&1)res=res*x%mod;
        x=x*x%mod;
        n>>=1;
    }
    return res;
}
ll inv(ll a,ll p){return pow_mod(a,p-2,p);}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n,m,c;
    cin>>n>>m>>c;
    ll ans=0;
    for(int i=0;i<m;i++){
        ans+=pow_mod(c,n*n*__gcd(i,m),mod);
        ans%=mod;
    }
    cout<<ans*inv(m,mod)%mod<<endl;
    return 0;
}

C.Joyride （分层图最短路）

题意

C：游乐场有n个设施，有m条人行道，游乐设施会花费ti的时间和pi的钱，人行道需要花费t的时间，你需要用最少的钱恰好游玩x的时间，起点是1，终点是1，求最少的钱是多少4

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e3+50;
const int inf=1e9+7;
int x,n,m,t;
vector<int>ve[maxn];
struct need{
  int t,p;
}ned[maxn];
struct node{
    int in;
    int w;
    int time;
};
int dis[maxn][maxn];
void dij(){
    queue<node>q;
    q.push(node{1,ned[1].p,ned[1].t});
    for(int i=0;i<=1000;i++){
        for(int j=0;j<=1000;j++)dis[i][j]=inf;
    }
    dis[1][ned[1].t]=ned[1].p;
    while(!q.empty()){
        node now=q.front();
        q.pop();
        int in=now.in,w=now.w,time=now.time;
        if(time+ned[in].t<=x&&w+ned[in].p<dis[in][time+ned[in].t]){
            dis[in][time+ned[in].t]=w+ned[in].p;
            q.push(node{in,dis[in][time+ned[in].t],time+ned[in].t});
        }
        for(int i=0;i<ve[in].size();i++){
            int nex=ve[in][i];
            int nextime=time+t+ned[nex].t;
            if(nextime<=x&&dis[nex][nextime]>w+ned[nex].p){
                dis[nex][nextime]=w+ned[nex].p;
                q.push(node{nex,w+ned[nex].p,nextime});
            }
        }
    }
}

int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    cin>>x>>n>>m>>t;
    for(int i=1;i<=m;i++){
        int a,b;
        cin>>a>>b;
        ve[a].push_back(b);
        ve[b].push_back(a);
    }
    for(int i=1;i<=n;i++){
        cin>>ned[i].t>>ned[i].p;
    }
    dij();
    if(dis[1][x]==inf)cout<<"It is a trap."<<endl;
    else cout<<dis[1][x]<<endl;
    return 0;
}

D.Pants On Fire (map+dfs,or 传递闭包)

题意

D 有n个已知串，给m个串，让你去判断他们是对的还是错的还是未知的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e3+50;
const int inf=1e9+7;
map<string,int>mp;
int cnt;
bool ok[500][500];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    string a,b,c,d,e;
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>a>>b>>c>>d>>e;
        if(!mp[a])mp[a]=++cnt;
        if(!mp[e])mp[e]=++cnt;
        ok[mp[a]][mp[e]]=true;
    }
    for(int k=1;k<=cnt;k++){
        for(int i=1;i<=cnt;i++){
            for(int j=1;j<=cnt;j++){
                ok[i][j]|=ok[i][k]&&ok[k][j];
            }
        }
    }
    for(int i=1;i<=m;i++){
        cin>>a>>b>>c>>d>>e;
        if(!mp[a]||!mp[e]){cout<<"Pants on Fire"<<endl;continue;}
        int u=mp[a],v=mp[e];
        if(ok[u][v])cout<<"Fact"<<endl;
        else if(ok[v][u])cout<<"Alternative Fact"<<endl;
        else{
            cout<<"Pants on Fire"<<endl;
        }
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e3+50;
const int inf=1e9+7;
map<string,int>mp;
int cnt;
vector<int>G[maxn];
bool dfs(int u,int v){

    for(int i=0;i<G[u].size();i++){
        if(G[u][i]==v)return true;
        bool ok=dfs(G[u][i],v);
        if(ok)return true;
    }
    return false;
}
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    string a,b,c,d,e;
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>a>>b>>c>>d>>e;
        if(!mp[a])mp[a]=++cnt;
        if(!mp[e])mp[e]=++cnt;
        G[mp[a]].push_back(mp[e]);
    }
    for(int i=1;i<=m;i++){
        cin>>a>>b>>c>>d>>e;
        if(!mp[a]||!mp[e]){cout<<"Pants on Fire"<<endl;continue;}
        int u=mp[a],v=mp[e];
        if(dfs(u,v))cout<<"Fact"<<endl;
        else if(dfs(v,u))cout<<"Alternative Fact"<<endl;
        else{
            cout<<"Pants on Fire"<<endl;
        }
    }
    return 0;
}

F.Plug It In (匈牙利算法/二分图匹配/网络流)

题意

m个插口，n个电器 k个可以匹配的连接 ,问你最大匹配数，但是你有一次机会把一个接口变成三个一样的

思路

考虑暴力每次暴力把一个其中一个接口数+2跑匈牙利算法，复杂度N^3，然后发现其实第一次跑的最初的图是可以一直重复利用的，然后就直接把后面的多出来的接口拿去跑增广路就行。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=3e5+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
/// 二分图最大基数匹配

int mp[1550][1550];
int link[1550];
int n,m,k;
bool vis[1550];
int remain[1550];
bool match(int u){
    for(int i=1;i<=m;i++){
        if(vis[i]==0&&mp[u][i]){
            vis[i]=1;
            if(link[i]==-1||match(link[i])){
                link[i]=u;
                return 1;
            }
        }
    }
    return 0;
}


int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int k;
    cin>>n>>m>>k;
    memset(link,-1,sizeof(link));
    for(int i=1;i<=k;i++){
        int a,b;
        cin>>a>>b;
        mp[a][b]=1;
    }
    int ans=0;
    for(int i=1;i<=n;i++){
        memset(vis,0,sizeof(vis));
        if(match(i))ans++;
    }
    for(int i=1;i<=m;i++){
        remain[i]=link[i];
    }
    int mx=0;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++)mp[n+1][j]=mp[n+2][j]=mp[i][j];
        for(int i=1;i<=m;i++){
            link[i]=remain[i];
        }
        int now=0;
        memset(vis,0,sizeof(vis));
        for(int j=n+1;j<=n+2;j++){
            if(match(j))now++;
        }
        mx=max(now,mx);
    }
    cout<<ans+mx<<endl;
    return 0;
}

G.Water Testing (皮克定理)

题意

给你一个多边形问你多边形中的整点个数有多少

思路

皮克定理

皮克定理是指一个计算点阵中顶点在格点上的多边形面积公式，该公式可以表示为2S=2a+b-2，其中a表示多边形内部的点数，b表示多边形边界上的点数，S表示多边形的面积。

其中，面积用每两条线的叉积计算

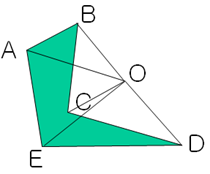
image

当O点为原点时，根据向量的叉积计算公式，各个三角形的面积计算如下：

S_OAB = 0.5(A_xB_y - A_y*B_x) 【(A_x，A_y)为A点的坐标】

S_OBC = 0.5(B_xC_y - B_y*C_x)

S_OCD = 0.5(C_xD_y - C_y*D_x)

S_ODE = 0.5(D_xE_y - D_y*E_x)

S_OEA = 0.5(E_xA_y - E_y*A_x)

边界的点数用gcd(a.x-b.x,a.y-b.y)计算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=3e5+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
struct Point{
    ll x,y;
}my[maxn];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n;
    cin>>n;
    for(int i=0;i<n;i++){
        cin>>my[i].x>>my[i].y;
    }
    ll s=0,b=0;
    for(int i=0;i<n;i++){
        s+=my[i].x*my[(i+1)%n].y-my[(i+1)%n].x*my[i].y;
        b+=__gcd(abs(my[i].x-my[(i+1)%n].x),abs(my[i].y-my[(i+1)%n].y));
    }

    s/=2;
    s=abs(s);
    cout<<s-b/2+1<<endl;
    return 0;
}

I.Uberwatch (基础DP)

思路

对于每个点考虑两种情况，如果他不放必杀技那

如果他放必杀技，那么他就只能在i-m时间之前放的最大值加起来

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=3e5+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int a[maxn];
int dp[maxn];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    int sum=0;
    for(int i=m+1;i<=n;i++){
        dp[i]=max(dp[i-1],dp[i-m]+a[i]);
    }
    cout<<dp[n]<<endl;
    return 0;
}

K.You Are Fired (签到)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e5+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
struct node{
    ll money;
    string name;

}my[maxn];
bool vis[maxn];
int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);
    ll n,d,k;
    cin>>n>>d>>k;
    for(int i=1;i<=n;i++){
        cin>>my[i].name>>my[i].money;
    }
    sort(my+1,my+1+n,[](node a,node b){
        return a.money>b.money;
    });
    ll ans=0,num=0;
    for(int i=1;i<=k;i++){
        ans+=my[i].money;
        vis[i]=true;
        num++;
        if(ans>=d)break;
    }
    if(ans<d)cout<<"impossible"<<endl;
    else{
        cout<<num<<endl;
        for(int i=1;i<=n;i++){
            if(vis[i])
            cout<<my[i].name<<", YOU ARE FIRED!"<<endl;
        }
    }
    return 0;
}